O

kreślenie F.G- nowa nauka, pojawiła się w latach 60. Metody badania bliskie fizyce ciała stałego. Stosowane zasady teorii podobieństwa

Statystyki matematycznej, wykorzystuje zależności korelacyjne. Miejsce F.G. określone jest jej obiektem badań, bez znajomości składu mineralnego, wł. strukturalnych skał, oraz warunków ich zalegania możliwe jest badanie fizycznych wł. skał i masywów skalnych.

Fiz.Górotw.- to nauka o fizykotech. wł. skał i procesach w nich przebiegających, a wywołanych działalnością górniczą, współzależnościami między nimi i zasadami ich wykorzystywania przy rozwiązywaniu zadań związanych z technologią urabiania.

Zadania F.G - 1)badanie fiz. wł. skał; ustalenie wartości fiz.-chem parametrów, 2)ustalenie zależności zmian wł. fiz w warunkach zewnętrz. Oddziaływania pól fizycznych, 3)ilościowy opis procesów fiz. w górotworze, 4)badanie przebiegu procesów w górotworze;

a)opracowanie nowych metod oddziaływania na skały pozwalających zmieniać ich wl. fiz przez ochładzanie, ogrzewanie, nasycanie cieczą

b)opracowanie nowych technologii urabiania i rozdrabniania, z wykorzystaniem oddział. mech., termicznego, magnetycznego.

c) stworzenie systemów kontroli składu, budowy i zachowania się skał w procesach związanych z działalnością górniczą

Termicz. własności skał - charakteryzują proces rozchodzenia się i pochłaniania ciepła w skałach, warunkiem przepływu ciepła jest nierównomierny rozkład temp. w skale. Przez ciepło rozumie się sumę średniej energii kinet. cząstek skały, natomiast przez temp. pewną miarę tej energii. Przeplyw odbywa się: 1)na drodze kondukcji w fazie stałej 2)na drodze konwekcji w fazie ciekłej i gazowej 3)na drodze radiacji we wszystkich fazach.

W ciałach jednorodnych przekazywanie ciepła odbywa się na drodze zmiany en. kinet przy zderzeniach elektronów, ten typ przewodności nosi nazwę ELEKTRONOWEJ jest charakt. dla metali i półprzewodników. W ośrodku skalnym przekazywanie ciepła odbywa się zwykle przez drganie siatki krystal, ten typ przew. można identyfikować do drgań FONONÓW.

Fonony - to kwanty pola drgań siatki kryst., każdy F jest podobny do fotonu pola elektromag., posiada określoną energię i częstotliwość drgań. W skałach mamy więc do czynienia z przewodnością fononową.

Wsp. przewodz. ciepła - jest to ilość ciepła Q przechodząca w jedn. czasu  przez jedn. przekroju poprzecz. F przy gradiencie temp. = jednostce w przypadku stacjonarnego strumienia ciepła

λ=

Cieplna opor. właściwa - to odwrotność wsp. przew.ciepła. Charakteryzują zdolność skał do przekazywania ciepła

Wsp. anizotropii - stosunek cieplnej oporności wł. mierzonej prostop. do uwarstwienia, do oporności mierzonej równolegle.

Cieplna poj. właściwa - charakteryzuje pochłanianie ciepła przez skałę, tzn. zwiększenie energii wewn. części siatki krystalicznej, jest równa ilości ciepła Q potrzebnego do podwyższenia temp. jednostki masy o 1 st.

C=

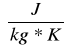
Pojem. cieplna objęt. - to ilość ciepła potrzebna do zmiany temp. jednostki objętości o 1 st.

Wsp. przew. temp.- charakt. prędkość rozchodzenia się temp. w skale. wsp.  i a charakt .izolacyjne własności skał, a zależą od udziału poszczególnych faz, od cech strukt. i tekst., od stanu wilgotności i temperatury

a=

Wsp. cieplej rozszerz. liniowej - to zmiany przyrostu próbki skalnej z przyrostem temp., ciepło pochłonięte przez skłę zużyte na ogrzanie i pracę wewn. związaną z rozszerzalnością cieplną.

Wsp. cieplej rozszerz. objętośc. - to zdolność skały do zmiany swej objętości podczas przyrostu temp.

Napręż. termiczne - powstają w wyniku nierównomiernego nagrzewania bądź rozszerzenia ziarn mineral. Przy uwzględnieniu tylko rozszerzalności :

• liniowej
  

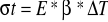
• objętościowej
  

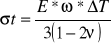
Stopień geoterm. - to liczba metrów, przy której temp. wzrasta o 1 st.

Gradient geoterm. - liczba stopni o jaką temp. wzrasta na 1m gł. Stały wzrost temp. zgodnie z gradientem następuje dopiero od tzw. Warstwy neutralnej, która w Polsce waha się od 15-20m.

Temp. panująca na głeb. X - T=T_O+G(H-H_O) b) dla skał niejednorodnych nie ma to charakt. Prostoliniowego T=T_O+(H-H_O)^B

Przepływ kondukcyjny - to przechodzenie ciepła wewnątrz poszczególnych ziaren min. Przepływ następuje w miejscach ich styku, w lepiszczu międzyziarnowym a wymiana ciepła na granicy ziaren min. i płynów.

Przepływ konwekcyjny - przepływ ciepła w płynach wypełniających pory

Droga promieniowania - przepływ przez promieniowanie jest możliwy, gdy temp. skaly jest ok.1000 st. Kelwina.

Ilość ciepła Q_c przepływającego od pow. skały o wyższej temp. T₁ do pow. o niższej T₂, przez pole S w czsie T w przypadku przepływu ustalonego w czasie Q_c=_(__X₁-X₂)*ST _c - wsp. przewodzenia ciepła

Gęstość pow. strum. ciepła - ilość ciepła przepływającego w jednostce czasu przez jednostkę pola pow.

j_c =
.

ODDZIALYWANIE PÓL CIEPLNYCH NA SKAŁY

1.związany z pojawieniem się w skalach naprężeń term. Podczas nierównomiernego podgrzewania poszczególnych cząstek skały, lub nierównomiernego rozszerzania poszczególnych ziarn. Jeśli pewna objętość skały zostanie nagrzana lub ochłodzona równomiernie, to w niej również mogą powstać wewn. naprężenia cieplne. Przy cyklicznych zmianach temp. naprężenia te są przyczyną odksztalceń, a nawet przyczyną rozpadu skał, co można wykorzystać w termicznych metodach urabiania.

2. uzależnione jest od termochem. przemian minerałów w skałach. Wyróżniamy przemiany:

a)wysychanie skały przez usunięcie wody wolnej

b)przejście skały z jednego stanu w drugi

c)przejście min. z jednej formy kryst. w inną bez zmian ich składu chem.

d)dehydratacja (usunięcie wody chem. związanej)

e)dysocjacja (samorzutny rozpad min. na mniejsze cząstki podczas ogrzewania z wydzieleniem fazy gazowej

f)utlenianie i redukcja

Największy spadek wartości modułu E obserwuje się do temp. ok. 600st. W skalach zawieających węgiel wysoka temp. prowadzi do wypalenia skały. Moduł sprężystości postaciowej G, w miarę wzrostu temp. skał maleje i przy temp. topnienia wynosi 0.

OCHŁADZANIE

Następuje zwiększenie modułu E w wyniku zamarzania wody wypelniającej pory i wzmacniania się wiązań miedzycząst

SORBCJA I ADSORBCJA.

Sorpcja obejmuje: 1)adsorpcję- pochłanianie subst. na pow. podziału 2)absorpcję- pochłanianie subst. przez całą obj. Ciała pochłaniającego

Zdolność skały do sorbowania pary wodnej nazywa się higroskopijnością. W wyniku sorbcji następuje zmiana stężenia substancji w porach.

Uzupełnienie tego stężenia do wartości pierwotnej lub wyrównanie stężeń może nastąpić w wyniku przepływu cieczy lub gazu.

A_s= A_sr[1-exp(-ks)] - to ilość substancji A_s zaadsorbowana na jednostkę masy adsorbentu w czasie  od chwili początku adsorbcji.

A_sr- równowagowa ilośc substancji zaadsorbowanej

ks- stała zależna od pow. adsorbenta

Sorpcja prowadzi do lokalnych zmian stężenia cieczy lub gazów, różnica stężeń wywołuje dyfuzję substancji wypełniających pory.

M = -Ddρ
*SΔT- ilość masy substancji migrującej w skale z miejsca o wyższym stężeniu C1 do miejsca o niższym stężeniu C2, przez pole S w czasie T.

Ilość masy przenoszonej w jednostce czasu przez jedn. pow. nazywa się gęstością pow. strumienia masy Im=
[kg/m²*s]

Pory w skale mogą mieć różną średnicę, i różny stopień wzajemnej łączności, z tego powodu wartość wsp. dyfuzji ocenia się na podstawie badania kinetyki procesu sorpcyjno - dyfuzyjnego. Proces ten, jak i zjawisko pęcznienia można scharakteryzować poprzez wsp. rozszerzalności stężeniowej _c . Określa on związek między przyrostem stężenia C subst. adsorbowanej w skale.

c = c (C-Co)ⁿ = c (C)ⁿ

Nierównomierność pęcznienia skały, związana jest z niejednorodnością pola stężeń, oraz anizotropią rozszerzalności stężeniowej. Wymienione parametry są przyczyną powstania naprężeń stężeniowych w skale. Rozpatrujemy próbkę skały jednorodnej w kształcie walca w której przebiega proces sorpcyjno - dyfuzyjny. Jeżeli końce pręta są swobodne, to wzrost stężenia substancji sorbowanej w skale o wartość C spowoduje wzdłużne odkształcenie pręta c = c*C, w pręcie którego oba końce są przymocowane do nieruchomych i nieodkształcalnych płyt wzrost stężenia o C wywoła naprężenia ściskające stężeniowe σ_c = _c*E*C .

WPŁYW WILGOCI NA WŁ. FIZ.

Nasycenie skały wodą ułatwia jej zniszczenie przy znacznie mniejszych naprężeniach, niż w wypadku skał suchych. Woda pod działaniem zewn. Ćiśnienia dąży do rozprzestrzeniania się w całej objętości skały, naruszając więzi między cząstkami, rozszerzając szczeliny, przeciwdziałając się ich zamykaniu. Mierząc przyrost masy próbki pochłaniającej wilgoć z powietrza, aż do chwili ustalenia się równowagi, czyli pełnego nasycenia wilgocią uzyskuje się charakterystykę kinetyki sorpcji.

Nasycone wodą gliny, iły stają się plastyczne, ich wytrzymałość na ściskanie spada. Zawilgocenie skał porowatych prowadzi do wzgl. Wzrostu wsp. przewodnictwa cieplnego . Przy niewielkim wzroście nawilgocenia, przewodnictwo temp. wzrasta, przy dalszym wzroście wilgotności obniża się w wyniku wpływu pojemności cieplnej. Innym parametrem może być opór elektr. W dobrych przewodnikach, będących w stanie suchym, przewodnictwo elektr. Ze zmianą wodonasycenia zmienia się w niewielkich granicach, natomiast w złych przewodnikach bardzo silnie. Na wielkość oporu elektr. Wpływa nie tylko woda, ale również stopień jej mineralizacji.

POLE WIELKOŚCI FIZYCZNYCH

Obszar przestrzeni, w którym każdemu punktowi przyporządkowana jest jedna lub więcej liczb określających jakąś wielkość fizyczną. Wszystkie wielkości określające jedną wielkość fizyczną tworzą tzw. Pole fizyczne. Funkcja dokonująca przyporządkowania danej wielkości do pola fizycznego nazywamy funkcją pola. Zakładamy, że funkcja ta w otoczeniu danego punktu jest jednowartościowa, ciągła i różniczkowalna.

RODZAJE PÓL FIZYCZNYCH:

- stacjonarne czyli ustalone w czasie i zaliczamy do nich takie, jeżeli określona wielkość fiz. zależy jedynie od położenia, nie zmienia się w czasie

- niestacjonarne zmienne w czasie, jeżeli określona wielkość fizyczna zależy nie tylko od położenia, ale również od parametru czasu. Jeżeli w każdym punkcie obszaru rozważana wielkość jest taka sama, pole fizyczne nazywamy jednorodnym. Rozważana wielkość nie zależy od położenia. Rozważane pole fizyczne zależy od przyjętego układu współrzędnych: prostokątnych, walcowych, kulistych. Jeżeli rozważana wielkość zależy tylko od dwóch współrzędnych to mówimy wtedy o płaskim polu fizycznym.

RODZAJE WIELKOŚCI FIZYCZNYCH ze względu na charakter geometryczny:

Skalar, wektor, tensor.

O tym, czy dana wielkość fizyczna jest skalarem, wektorem, czy tensorem decyduje nie tylko ilość liczb opisująca daną wielkość, ale również zachowanie się tej wielkości względem transformacji układu współrzędnych tzn. przesunięcia, obrotu, odbicia.

Skalar - wielkość określona jedną liczbą, która nie zmienia się przy jakiejkolwiek zmianie układu współrzędnych. Skalar jest więc niezmiennikiem.

Wektor - w przestrzeni trójwymiarowej taka wielkość fizyczna o trzech składowych, której składowe spełniają warunki: -przy przesunięciu równoległym pozostają niezmienne, -przy obrocie zmieniają się, -przy odbiciu lustrzanym składowa prostopadła do płaszczyzny odbicia zmienia znak.

Tensor - drugiego rzędu w przestrzeni trójwymiarowej, wielkość fizyczna określona 9 składowymi, które zachowują się: -są niezmienne przy przesunięciu równoległym,

-zmieniają się przy obrocie,

-zmieniają znak przy odbiciu lustrzanym, z wyjątkiem składowych przekątnych.

MIARY NIEJEDNORODNOŚCI PÓL FIZYCZNYCH.

Czynnikiem warunkującym przebieg procesów fizycznych w rozważanym obszarze jest niejednorodność pól fizycznych.

POLE SKALARNE

Rozważamy płaskie pole zadane w prostokątnym układzie współrzędnych. W polu tym można wyznaczyć linie, na których rozważana wielkość skalarna posiada jednakową wartość. Są to tzw. izolinie pola lub linie ekwiskalarne (izotermy, izobary). Pochodne cząstkowe określają szybkość zmiany wielkości w kierunku osi x i y. Sumując wektorowo zmiany wielkości skalarnej w kierunku x i y otrzymuje się wielkość grad a (wektor):

Kierunek tego wektora wyznacza kierunek największej zmiany pola skalarnego, natomiast jego wartość określa wielkość zmiany pola skalarnego w danym punkcie przestrzeni. Jeżeli pole skalarne jest jednorodne tzn. a=const, grad a = 0. Wielkość wektorową grad a można uważać za lokalna miarę niejednorodności pola skalarnego. Operator różniczkowy gradient przypisuje dowolnemu polu skalarnemu odpowiednie pole wektorowe grad a. Dla oznaczenia operatora różniczkowego grad używa się często symbolu nabla
. Takie ujęcie pozwala w sposób formalny oddzielić gradient od skalara a i na odwrót, pozwala uznawać formalnie wektor
za wynik mnożenia składowych wektora nabla przez skalar a.

POLE WEKTOROWE

Rozważamy płaskie pole wektorowe zadane w prostokątnym układzie współrzędnych x,y. W polu tym nie można wyznaczyć bezpośrednio izolinii ponieważ wielość wektorowa u określa dwie jego składowe u_x i u_y, a każda w zadanym obszarze może zmieniać się inaczej. Dla określenia miary niejednorodności pola wektorowego należy oddzielnie zbadać zmianę składowej u_X wzdłuż osi x i y oraz zmianę u_Y wzdłuż osi x i y. Wielkość tych zmian określają odpowiednie pochodne cząstkowe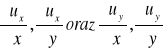

W przypadku płaskiego pola wektorowego miarę niejednorodności stanowić będzie wielkość o czterech składowych zwana gradientem lecz oznaczona Grad u

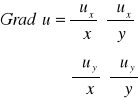
Rozważania przenieść można również na przestrzenne pole wektorowe.

Wielkość Grad u jest tensorem drugiego rzędu dlatego też zwana jest gradientem tensorowym. Operator różniczkowy Grad przypisuje dowolnemu polu wektorowemu pole tensorowe gradient u. Gdy pole wektorowe jest jednorodne tzn dla u=const to Grad u=0. Wielkość tensorowa Grad u jest lokalną miarą niejednorodności pola wektorowego. Gradient tensorowy można wyrazić przez operator wektorowy nabla.

Oprócz tensorowej miary niejednorodności w polu wektorowym możemy określić drugą skalarną miarę niejednorodności tego pola. miara ta określona iloczynem skalarnym wektora
i wektora U . Określona w ten sposób wielkość skalarną nazywamy dywergencją lub rozbieżnością pola wektorowego. Operator różniczkowy div przypisuje dowolnemu polu wektorowemu U pole skalarne dywergencją

Gdy pole wektorowe jest jednorodne, czyli u = const to div u = 0. W dowolnym polu wektorowym można określić dwie miary niejednorodności pola:

-miarę tensorową Grad u

-miarę skalarną div u.

UKŁAD FIZYCZNY.

Nazywamy wyodrębnioną do badań organiczną część przestrzeni materialnej, czyli pewien obszar górotworu, który może reagować w określony sposób na jakieś zewnętrzne oddziaływania. Pomiędzy układem a otoczeniem znajduje się osłona posiadająca różne własności fizyczne. Gdy osłona doskonale oddziela układ od otoczenia mówimy wtedy, że układ jest izolowany.

PARAMETRY UKŁADU

Parametry ekstensywne - są to te wielkości, które związane są z wymiarami przestrzennymi układu fizycznego, a ich pomiar obejmuje cały układ np. masa układu, energia układu, ładunek elektryczny. Cechą charakterystyczną wielkości ekstensywnych jest ich sumowanie się.

Parametry intensywne - mają charakter lokalny, można je więc mierzyć w określonym miejscu danego układu. Wielkości intensywne przy połączeniu dwóch układów wyrównują się a nie dodają. Gęstość masy będąc parametrem intensywnym jest zarazem ilorazem dwu wielkości ekstensywnych. Wszystkie wielkości, które są ilorazem dwu wielkości ekstensywnych są wielkościami intensywnymi.

PROCES FIZYCZNY.

Jeżeli w rozważanym układzie fizycznym nie zachodzą zmiany parametrów i nie występują żadne przepływy wówczas mówimy, że układ jest w równowadze. W wyniku zewnętrznego oddziaływania otoczenia na układ lub przemian zachodzących w samym układzie mogą zmienić się wartości parametrów układu, mogą też występować przepływy wielkości ekstensywnych. Zjawisko zmiany parametrów układu lub występowania przepływów nazywamy procesem fizycznym. Proces ten polega na przepływie wielkości ekstensywnych i wyrównaniu się wielkości intensywnych.

ODDZIAŁYWANIA FIZYCZNE.

Mechaniczne objętościowe, w którym charakt. wielkością ekstensywną jest skalarna wielkość objętości. Rozpatrujemy układ odizolowany od otoczenia, który dzielimy na dwa podukłady rozdzielone przegrodą, która może się przesuwać. W podukładzie 1 panuje ciśnienie p₁>p₂, wówczas ścianka się przesuwa do wyrównania ciśnień. Podukład 1 traci energię, jego objetość wzrasta, a ciśnienie maleje. Oprócz przepływu objętości nastąpił przepływ energii, ale energia całkowita została bez zmian. Iloraz dwu wielkości ekstensywnych jest wielkością intensywną

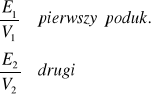
Przy wzroście ciśnienia objętość maleje, stąd za charakterystyczną wielk.intens.uznaje się wartość ujemną ciśnienia.

Mechaniczne reologiczne

Zakładamy, że dwa układy poruszają się wzdłuż jednej prostej w tą samą stronę. Układ 1 porusza się z prędkością v₁ i masą M₁, a drugi V₂,M₂. Jeżeli V₁>V₂, to w określonej chwili oba układy zetkną się. Z układu 1 do 2 przepływać będzie pęd i energia do chwili V₁=V₂. Pęd jako iloczyn masy i prędkości oraz energia są wielk.ekstens. zachowawczymi.

V₁,M₁+ V₂,M₂=

E₁+E₂=

Prędkość jest charakt.wielk.intensywną w oddziaływaniu mech.reologicznym, gdyż wyznacza kierunek procesu przepływu i energii oraz określa warunek równowagi procesu. Przepływ pędu odbywa się gdy poszczególne cząstki mają różne prędkości. W tym oddziaływaniu wielkość charakt.jest wektorem w pozostałych są to skalary.

Oddziaływanie subst chemicznej

Rozpatrujemy układ odizolowany od otoczenia. Wyróżniamy dwa podukłady rozdzielone przegrodą nieruchomą lecz przenikliwą dla masy. Przenikanie masy trwa tak długo, aż wyrównają się wielkości intensywne czyli potencjały chemiczne układu. Początkowa potencjał chemiczny układu 1 jest większy od 2, po zakończeniu wymiany wyrównują się. Przechodząca masa przenosi również energię. Zarówno masa jak i energia są wielkościami ekstensywnymi zachowawczymi. Zachowawcza jest całość energii a nie poszczególne formy.

Oddziaływanie elektrostatyczne

Zakładamy układ odizolowany oddzielony przegrodą nieruchomą, nieprzenikliwą dla masy, ale jest przewodnikiem ładunku elektrycznego. Jeżeli potencjał elektrostatyczny układu 1 jest większy od 2, to z układu 1 do 2 przepływa przez osłonę ładunek elektryczny unosząc również ze sobą energię. Przepływ ładunku i energii trwa do wyrównania się potencjałów. W tym oddziaływaniu zarówno ładunek elektryczny jak i energia są wielkościami zachowawczymi.

Oddziaływanie termiczne

Układy rozdzielone nieruchomą, nieprzenikliwą dla masy, ale przewodząca energię cieplną przegrodą, posiadają różne temperatury. Przepływ trwa tak długo, aż temperatury wyrównają się. Energia jest wielkością zachowawczą. W tym oddziaływaniu wraz z energią nie przepływa żadna inna zachowawcza wielkość ekstensywna. Drugą wielkością ekstensywną lecz niezachowawczą jest entrpoia S₁+S₂<

Energia się rozprasza, a entropia rośnie. W części izolowanej od otoczenia ilość stracona przez jeden układ jest mniejsza od ilości zyskanej przez drugi, dotyczy to procesów rzeczywistych i jest ilościowym wyrazem II zasady termodynamiki -ΔS₁=-S₂.

---