Wykład I.2: Dobór próby do badań.

Plan:

1. Populacja badana. Badania wyczerpujące i nie wyczerpujące.

2. Etapy doboru próby

3. Określenie liczebności próby losowej

4. Określenie liczebności próby nielosowej

1. Populacja badana. Badania wyczerpujące i nie wyczerpujące.

Populacja badana - to skończona zbiorowość, o której badacz chce uzyskać określone dane.

Badania populacji - mogą być:

• wyczerpujące - obejmujące całą populację badaną;

• nie wyczerpujące.

Badania rynku, w których gromadzi się informacje pierwotne - niezwykle rzadko obejmują całą badaną zbiorowość (populację generalną). Są możliwe głównie w przypadku populacji małych lub bardzo małych.

Przykładami badań niepełnych są: sondaż, ankieta, eksperyment.

W badaniach nie wyczerpujących zachodzi potrzeba doboru próby, na której badania zostaną przeprowadzone.

Próbą (zbiorowością próbną) nazywamy część zbiorowości generalnej, wybraną za pomocą metod naukowych , uczestniczącą w przeprowadzanych badaniach i reprezentującą zbiorowość w odniesieniu do przedmiotu badania.

2. Etapy doboru próby:

1/. określenie populacji badanej,

2/. określenie wykazu populacji badanej (operatu losowania),

3/. wybór metody doboru próby,

4/. określenie liczebności próby,

5/. zaplanowanie i pobranie próby.

2.1. .Określenie populacji badanej (zbiorowości generalnej, populacji generalnej).

Program badania powinien zawierać ścisłą identyfikację populacji objętej badaniem. Wielkość i rodzaj tej populacji zależy od ustalonego celu badania. Bez sprecyzowania celu badania nie można określić ściśle populacji.

Przy identyfikacji zbiorowości statystycznej należy odpowiedzieć na następujące pytania: kogo, lub co badamy? kiedy i gdzie badamy?

Na te pytania odpowiadamy, ustalając 3 cechy stałe badanych jednostek:

rzeczową, czasową, przestrzenną.

Cecha rzeczowa (przedmiotowa) - przesądza o tym, kto lub co jest przedmiotem badania. Cecha ta decyduje więc, jaka grupa osób, przedmiotów, zjawisk będzie stanowić zbiorowość generalną.

Cecha czasowa - określa, z jakiego okresu (lub momentu) przyjęto jednostki statystyczne. Uwzględniony w badaniu okres może być różny (długi lub krótki), decyduje o tym przede wszystkim cel badania i charakter zbiorowości.

Cecha przestrzenna - decyduje o tym, z jakiego obszaru (terytorium) gospodarczego, administracyjnego itp. jednostki powinny być włączone w skład zbiorowości.

Fakt, że cechy stałe są jednakowe u wszystkich jednostek zbiorowości statystycznej powoduje, że nie są one badane; badane są natomiast cechy zmienne. Nieodzowną właściwością zbiorowości statystycznej jest występowanie co najmniej jednej cechy różnicującej wewnętrznie tę zbiorowość (cechy zmiennej).

W definicji operacyjnej wyodrębnia się takie składniki populacji badanej jak: podmiot (element) badania, jednostkę próby, czas i miejsce, w którym jednostki próby będą poddane badaniom.

Przykład operacyjnej definicji populacji badanej:

Dla projektu badawczego dla dużego supermarketu w Krakowie:

• podmiot badania: głowa gospodarstwa domowego odpowiedzialna za dokonywanie większości zakupów w supermarkecie, tj. podejmująca samodzielnie decyzje o zakupie (kobieta lub mężczyzna);

• jednostka próby: gospodarstwo domowe;

• zakres przestrzenny: Kraków;

• czas: maj, 200 ..

2.2. Określenie wykazu populacji badanej

Wykaz badanej populacji (operat losowania) - jest to zbiór elementów tej populacji odwzorowany na określonej liście, z której dobiera się próbę.

Listą odwzorowującą badaną populację mogą być: księga adresowa, książka telefoniczna, lista wyborców, mapa lub jakikolwiek wykaz, spełniający następujące warunki aktualności, kompletności, wyłączności i dostępności.

Rzadko się zdarza, aby wykaz spełniał wszystkie wymagania. Występujące rozbieżności są źródłem błędów związanych z danym wykazem.

2.3. Wybór metody doboru próby

Przyjmuje się dwa rodzaje doboru próby:

• dobór losowy, przy którym tylko przypadek decyduje o tym, która jednostka zbiorowości generalnej będzie wylosowana. Cechą charakterystyczną tego doboru jest możliwość wnioskowania o charakterystykach populacji generalnej na podstawie zbadania losowo wybranej próby.

• dobór nielosowy (celowy). W sytuacji tej nie ma możliwości uznania próby za reprezentatywną względem określonych cech statystycznych, jak również możliwości przeprowadzenia wnioskowania statystycznego o zbiorowości generalnej. Sprawa jest dyskusyjna, gdyż występują argumenty na rzecz traktowania każdej obserwowanej statystycznie zbiorowości jako ”swoistej próby losowej” (np. szeregi czasowe realizacji obserwowanej zmiennej losowej).

Opis metod doboru próby losowej

1/- Dobór losowy prosty, w którym losuje się elementy próby bezpośrednio z populacji generalnej. Stosuje się go wtedy, gdy populacja jest niewielka liczebnie i nieznana jest jej struktura. (losowanie zależne i niezależne). -

2/- Dobór losowy systematyczny - jest odmianą doboru prostego, stosuje się go wówczas, gdy istnieje lista całej populacji generalnej. Polega na wyborze z uporządkowanego zbioru jednostek populacji odpowiedniej liczby jednostek w równych odstępach (interwałach).

Interwał losowania k = N /n ; N- liczebność populacji; n - liczebność próby.

3/- Dobór losowy warstwowy stosuje się w sytuacji, gdy jest znana struktura populacji generalnej. Pierwszym etapem jest jej podział na warstwy, które powinny być wewnętrznie jednorodne (ze względu na wyróżnioną cechę). Zróżnicowanie między warstwami - jak największe. W obrębie każdej warstwy dokonuje się oddzielnego, prostego doboru losowego.

Liczba jednostek losowanych z każdej warstwy powinna być z zasadzie proporcjonalna do liczebności warstwy.

Najczęściej stosowanymi kryteriami wyróżnienia warstw są: dochód, wielkość gospodarstwa domowego, wiek, płeć, wielkość miejscowości, pozycja społeczna.

4/- Dobór losowy grupowy (zespołowy)- w tym przypadku należy podzielić populację generalną w ten sposób, aby zróżnicowanie wewnątrz grup było jak największe, a pomiędzy grupami minimalne. Następnie dokonuje się losowego wyboru jednej z grup i dopiero po tym stosuje się losowanie proste lub warstwowe w celu wyboru podstawowych elementów do próby.

Metody doboru nielosowego

W tym przypadku możliwe jest określenie przez badacza, w sposób arbitralny, które z jednostek populacji generalnej znajdą się w próbie.

1/- Dobór kwotowy - należy do najczęściej stosowanych metod nielosowego doboru próby w badaniach rynku. Opiera się on na znajomości struktury populacji generalnej wg przyjętych cech (tzw. zmiennych kontrolnych) i

narzuceniu tej struktury na skład próby. Stosowane cechy -kryteria to: wiek, płeć, wielkość rodziny, dochód, rodzaj grupy społecznej lub działalności.

Liczebność grup (segmentów) w próbie ustala się na podstawie przemnożenia rozkładu procentowego wybranych cech w populacji generalnej przez ogólną liczebność próby.

Najczęściej poprzestaje się na 2 lub 3 cechach dających możliwość kwotowego określenia niewielkiej liczby segmentów. (Przy większej liczbie cech jako zmiennych kontrolnych i większej liczbie segmentów - trudniej skompletować odpowiedni skład zbiorowości próbnej).

2/- Dobór celowy („wg wygody”) - najbardziej typowy przypadek doboru nielosowego. Polega na całkowicie subiektywnym wyborze jednostek badanych do próby w nadziei uzyskania najszerszej i najpełniejszej informacji. Metoda stosowana w wywiadach psychologicznych a zwłaszcza głębinowych, a także w badaniach eksperymentalnych. Elementami próby są te obiekty, które wg badacza odpowiadają celom badań.)

3/- Dobór przypadkowy („przechwytywania po drodze”).. Polega na przypadkowym (na „chybił - trafił”) doborze pewnych jednostek, które w danej (przypadkowej) sytuacji znalazły się w dogodnym zasięgu.

4/- Inne metody:

Dobór jednostek typowych, dobór przez eliminację, losowanie sieciowe,

losowanie sekwencyjne.

3. Określenie liczebności próby losowej.

W zależności od tego jakim schematem losowania chcemy się posłużyć oraz jaki parametr populacji chcemy oszacować, stosuje się różne wzory na obliczenie liczebności próby.

Szacowane parametry są najczęściej wyrażane średnią arytmetyczną, lub częstością względną (tzn. proporcją, lub wartością procentową).

Błąd próby (d) - wyraża odchylenie parametrów próby od odpowiednich parametrów badanej zbiorowości.

Błąd średniej arytmetycznej z próby - wyraża odchylenie średniej arytmetycznej z próby od średniej arytmetycznej badanej zbiorowości.

Błąd wartości procentowej z próby - wyraża odchylenie częstości względnej z próby od częstości względnej badanej zbiorowości.

W badaniach rynku najczęściej przyjmuje się, że błąd próby powinien mieścić się w granicach  2%. Podobnie jak w przypadku określania poziomu ufności nie może to stanowić obowiązującej reguły; równie dobrze może zostać zaakceptowany błąd 5 lub 10%.

Przedział ufności - to przedział, który pokrywa prawdziwą nieznaną wartość parametru zbiorowości z określonym prawdopodobieństwem.

Poziom ufności (wyrażany w procentach [%]) - to prawdopodobieństwo pokrycia przez tzw. przedział ufności nieznanej wartości szacowanego parametru badanej zbiorowości.

3.1. Losowanie proste, niezależne (populacja nieskończona) - gdy szacuje się średnią populacji

(populacja nieskończona - gdy liczebność próby jest relatywnie mała w porównaniu z liczebnością populacji).

Przypadek najprostszy: populacja nieskończona, losowanie -niezależne, zakłada się znajomość przedziału ufności i odchylenia standardowego a badane zjawisko ma rozkład normalny

(1)

gdzie:

n - wielkość próby

u_ - liczba odchyleń standardowych, którą należy odczytać z tablicy rozkładu normalnego dla poziomu ufności 1- (wartość zmiennej standaryzowanej dla poziomu istotności )

δ - odchylenie standardowe badanej zmiennej w populacji (znane lub szacowane na podstawie wcześniejszych badań),

d- błąd średniej arytmetycznej z próby

Jeśli odchylenie standardowe s populacji jest nieznane, to należy je oszacować na podstawie małej próby (wstępnej) o liczebności n₀ i z wyników tej próby obliczyć średnią
oraz wariancję:

(2)

wówczas wzór na niezbędną liczebność próby ma nieco inną postać:

(3)

gdzie:

t_ - liczba jednostek odchyleń standardowych, którą należy odczytać z tablicy rozkładu Studenta dla poziomu ufności 1- i dla n₀ -1 stopni swobody,

s - odchylenie standardowe z małej próby,

d - dopuszczalny maksymalny błąd szacunku średniej m.

Jeśli obliczona na podstawie wzoru (3) liczebność właściwej próby n jest mniejsza od liczebności n₀, to liczebność wstępnej próby jest wystarczająca, jeśli zaś n jest większe od n₀, to należy dolosować do właściwej próby jeszcze n-n₀ elementów.

3.2. Losowanie proste niezależne (populacja nieskończona) - gdy szacuje się frakcję populacji (wskaźnik struktury, częstość względną).

W przypadku szacowania frakcji populacji a więc wskaźnika struktury, wzór na niezbędną liczebność próby jest następujący::

(4)

gdzie:

p - ocena frakcji populacji posiadającej wyróżnioną cechę,

q = 1 - p

d - błąd lub maksymalna różnica pomiędzy frakcją z próby a frakcją z populacji, którą chcemy przyjąć na obranym poziomie ufności,

u_ - liczba jednostek odchyleń standardowych, którą należy odczytać z tablicy rozkładu normalnego dla poziomu ufności 1 - .

W praktyce iloczyn pq szacuje się na podstawie wstępnej próby, której liczebność zależy od ocenianej frakcji p . Jeśli ta oceniana frakcja zawiera się w granicach 0,2<p<0,8, to wystarczy dla oszacowania iloczynu p(1-p) pobrać wstępną próbkę liczącą n₀ = 60 elementów. Jeśli natomiast szacowana frakcja p< 0,2, to należy pobrać tak dużą próbkę wstępną, aby n₀p = 25. Wówczas wzór na liczebność próby ma następującą postać:

(5)

gdzie:

t_ - liczba jednostek odchyleń standardowych, którą należy odczytać z tablicy rozkładu Studenta dla poziomu ufności 1- i dla n₀-1 stopni swobody.

Jeśli natomiast nie znamy wielkości szacowanej frakcji p, to wówczas przyjmujemy ją na poziomie p=1/2. Wówczas wariancja osiąga swój najwyższy poziom i wynosi pq = 1/4. Podstawiając tą wielkość do wzoru na liczebność próby otrzymujemy:

(6)

Jeśli prawdziwa wartość p będzie różniła się od przyjętego poziomu 1/2, to wówczas obliczona na podstawie wzoru (6) liczebność próby jest za duża, czyli stosując taką próbę otrzymujemy mniejszy błąd szacunku niż założono.

3.3. Określenie liczebności próby w przypadku losowania prostego zależnego (populacja skończona)

Jeśli populacja generalna ma skończoną liczbę N elementów, a rozkład badanej cechy x w populacji jest zbliżony do normalnego o średniej m i wariancji S², to wzór na niezbędną liczebność próby w przypadku losowania prostego, zależnego (gdy szacuje się średnią populacji) ma postać:

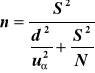
(7)

gdzie :

n - niezbędna liczebność próby

u_ - współczynnik zależny od przyjętego poziomu ufności (1-)

S - odchylenie standardowe badanej zmiennej w populacji (znane lub szacowane na podstawie wcześniejszych badań)

d - dopuszczalny max błąd szacunku średniej
(m)

N - liczebność populacji

Jeśli S jest nieznane, to należy je oszacować na podstawie małej próby (wstępnej) o liczebności n₀ dobranej w losowaniu zależnym i z wyników tej próby obliczyć średnią m oraz wariancję:

(8)

Wzór na niezbędną liczebność próby ma wówczas postać:

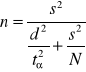
(9)

gdzie:

- odchylenie standardowe z małej próby.

3.4. Losowanie proste zależne (populacja skończona) - gdy szacuje się frakcję populacji

Wzór na obliczenie niezbędnej wielkości próby ma postać:

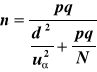
(10)

W praktyce szacuje się iloczyn p(1-p) na podstawie wstępnej próby, której liczebność zależy od ocenianej frakcji p. Wówczas wzór na liczebność próby ma postać:

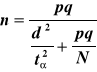
(11)

Jeśli nie znamy wielkości szacowanej frakcji p, wówczas przyjmujemy ją na poziomie p=1/2. Wtedy wariancja osiąga swój najwyższy poziom i wynosi pq=1/4. Podstawiając tą wielkość do wzoru (10) otrzymujemy:

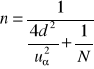
(12)

Jeśli prawdziwa wartość p będzie różniła się od przyjętego poziomu 1/2, to obliczona na podstawie wzoru (12) liczebność próby jest za duża, czyli stosując taką próbę otrzymujemy mniejszy błąd szacunku niż założono.

4. Określenie liczebności próby nielosowej

Wielkość próby stosowana w różnego typu badaniach marketingowych

Rodzaj badania	Typowa wielkość próby (liczba osób)	Minimalna wielkość próby (liczba osób)
Marketingowe badania rynku	1000 - 1500	500
Badania strategiczne	400 - 500	200
Test rynkowy	300 - 500	200
Test produktu (lub produktów)	200 - 300	200
Test nazwy	200 - 300	100
Test opakowania	200 - 300	100
Test reklamy telewizyjnej	200 - 300	150
Test reklamy radiowej	200 - 300	150
Test reklamy prasowej	200 - 300	150

---