ANALIZA DRGAŃ STRUNY
Cel: badanie kolejnych drgań harmonicznych struny pobudzanej metodą rezonansowa.
Przyrządy: elektromagnes , transformator , mikromierz .
Zagadnienia: drgania harmoniczne proste, podstawy akustyki
Wprowadzenie
Struna jest zawsze dwustronnie zamocowana i drga w jeden ze sposobów pokazanych na rysunku poniżej,
Rys.1.1 Różne możliwe sposoby drgań prętów i słupów powietrza.
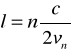
tylko w przypadku, gdy jest pobudzana częstością v dającą się obliczyć przez podstawienie (11,4) do (11.8b), przypadek a
Podstawiając na c wyrażenie otrzymamy
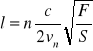
Gdy strunę pobudzamy do drgań w miejscu przypadkowym, występują w niej równocześnie wszystkie drgania spełniające warunek na górze a więc drgania harmoniczne o częstościach
![]()
Lub ogólnie
![]()
Każdy element struny wykonuje wtedy drganie wypadkowe powstałe wskutek nałożenia drgań harmonicznych prostych v1, V2,..., które nie jest już drganiem sinusoidalnym, lecz zachowuje nadal periodyczność. Stosując metodę szeregów Fouriera możemy to drganie zanalizować rozkładając na drgania składowe. Pobudzając strunę do drgań w miejscu przewidzianej strzałki i dobierając wartość siły F możemy pobudzić stronę do drgań z dowolną częstością vn.
Aparatura
a. Struna pozioma. Zasadniczą częścią przyrządu (rys 1) jest stalowa struna S. Pobudzana do drgań w sposób rezonansowy za pomocą elektromagnesu E zasilanego prądem przemiennym o częstości 50 Hz. Struna jest przyciągana przy każdym maksimum i minimum natężenia, a więc z częstością 100 Hz. Ze względu na dwustronne zamocowanie, struna wykonuje drgania pokazane na rysunku 1.1a jeżeli spełniony jest warunek (2). Celem dobrania siły F zastosowano wagę sprężystą W wraz z mechanizmem śrubowym M.
Rys 1 Przyrząd do analizy drgań struny stalowej.
Rys 2Przyrząd do analizy drgań struny pionowej.
śrubowym M. Amplitudę drgań odczytujemy na podziałce P1, a położenie elektromagnesu i podziałki P1, na podziałce P2. Bloczek B jest osadzony na łożysku kulkowym, dzięki czemu możemy zaniedbać tarcie. Dla wzbudzenia pierwszej harmonicznej
l (w = l) elektromagnes ustawiamy w połowie długości struny, dla n ==2 na 1/4 długości,
dla n = 3 na 1/6długości lub w połowie itd. Dla zwiększenia precyzji odczytu wychylenia należy stosować oświetlenie stroboskopowe (np. lampę jarzeniową).
b. Struna pionowa. W tym przyrządzie struną może być żyłka nylonowa lub nić. Jest ona pobudzana do drgań za pomocą płaskiej .żelaznej sprężyny Z. Dolny koniec tej sprężyny znajduje się między biegunami elektromagnesu E zasilanego prądem przemiennym. Sprężyna i elektromagnes stanowią części obwodu magnetycznego magnesu stałego lub elektromagnesu M. Zatem dolny koniec sprężyny jest stale biegunem magnesu (np. N) i w polu magnetycznym elektromagnesu E wykonuje drgania z częstością 50 Hz. (Sprężynę pobudzać można do drgań również w prostszy sposób, podobnie jak w przyrządzie z poziomą struną.) Dla uzyskania fali stojącej dobieramy obciążenie w taki sposób, by spełnione były warunki rezonansu. Przy dokładnym dobieraniu obciążenia, poza odważnikami, stosować możemy również piasek. Można również zamiast szalki zastosować naciąg sprężynowy. Do odczytywania amplitud i położenia strzałek wzdłuż struny służą podziałki Pl i P2. Struna jest rozciągnięta na tle matowej szyby M podświetlonej lampą jarzeniową dającą efekt stroboskopowy, co ułatwia odczyt amplitudy.
Pomiary
Sposób wykonania pomiarów nie zależy od typu stosowanego przyrządu. Jeżeli sprężyna W nie jest dynamometrem wyskalowanym, wzorcujemy ją wykonując pomiar zależności wydłużenia od obciążenia dla zakresu obciążeń wskazanych w instrukcji. Mierzymy długość i średnicę struny. Włączamy prąd w obwodzie elektromagnesu i siłę napinającą strunę oraz położenie elektromagnesu dobieramy w ten sposób, by uzyskać jedno z szukanych drgań harmonicznych. Analizujemy wynik pomiaru gęstości w oparciu o wzór (11.14a) i planujemy właściwy sposób pomiaru poszczególnych wielkości prostych. Wykonujemy ostateczne pomiary i mierzymy rozkład amplitud wzdłuż połowy długości fali stojącej dla l, 2 i 3-cich drgań harmonicznych.
Obliczenia
Wykreślamy przebieg zależności amplitudy drgań od położenia dla wszystkich badanych drgań harmonicznych. Na tym samym wykresie nanosimy sinusoidę o amplitudzie równej amplitudzie drgań struny i sprawdzamy zgodność punktów doświadczalnych z przebiegiem teoretycznym. Z wzoru (11.14) lub (11.8a) obliczamy gęstość struny dla każdej harmonicznej: Przyjmujemy, że częstość drgań jest znana i wynosi 100 Hz dla przyrządu omówionego w przypadku dla struny poziomej lub 50 Hz w przypadku dla struny pionowej. Ze wzoru (H.13) obliczamy prędkość rozchodzenia się fali w strunie. Jako wynik końcowy przyjmujemy wartości średnie q i c. Błędy obliczamy dla gęstości i prędkości dźwięku w oparciu o wyniki uzyskane dla l i 2-giej harmonicznej. Sprawdzamy wzajemną zgodność wyników obydwu harmonicznych oraz zgodność z tablicami fizycznymi.
10.01. DRGANIA HARMONICZNE PROSTE (Sl, § 43 i 44; Kl, rozdz. 7)
Drganiami harmonicznymi prostymi nazywamy drgania odbywające się pod wpływem siły F proporcjonalnej do wychylenia x i przeciwnie skierowanej.
F = -kx.
Współczynnik proporcjonalności k o wymiarze N • m -1 nazywamy silą kierującą. W przypadku drgań torsyjnych bryły sztywnej we wzorze powyższym siłę F należy zastąpić momentem siły M, a wychylenie x kątem skręcenia ϕ
M = - Dϕ (10.1)
Współczynnik proporcjonalności Z) o wymiarze N•m•rad-1 nazywamy momentem kierującym. W dalszym ciągu zajmiemy się wyłącznie drganiami torsyjnymi bryły sztywnej. Przytaczać będziemy również, wzory dla punktu, w których wychylenie będziemy oznaczać przez x. Korzystając z równania ruchu obrotowego bryły sztywnej, moment siły możemy wyrazić wzorem M =J⋅α
gdzie przez J oznaczone moment bezwładności, a przez a przyspieszenie kątowe, które definiujemy jako drugą pochodną kąta względem czasu
![]()
![]()
Podstawiając ostatnie dwa wyrażenia do równania (10.1) otrzymamy
![]()
i analogiczne równanie dla drgającego punktu o masie m,
Dzielimy równanie (10.2) przez J i wprowadzamy oznaczenie
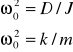
(10,3)
(10.3a)
(wielkość w o nazywa się częstością kołową drgań;, uzasadnienie tej nazwy znajdzie czytelnik w dalszych rozważaniach), otrzymując
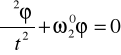
(10.4)
i
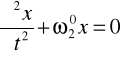
(10.4a)
Równanie powyższe nazywa się równaniem ruchu harmonicznego prostego. Jest ono równaniem różniczkowym drugiego rzędu względem^ zmiennej <p. Nietrudno sprawdzić, że rozwiązaniem powyższego równania jest funkcja
(10.5) (10.5a)
Wielkość δ nazywamy fazą początkową lub przesunięciem fazowym, a wielkość ϕ amplitudą.
Z własności funkcji trygonometrycznych wynika, że również funkcja
![]()
(10.6)
![]()
spełnia równanie (10.4); wtedy
Rozwiązaniem równania (10.4) jest również kombinacja liniowa obydwu funkcji trygonometrycznych
![]()
(10.6a)
![]()
Zależnie od potrzeby stosować będziemy jedną z wymienionych postaci rozwiązania. W obecnym paragrafie zastosujemy rozwiązanie w postaci równania (10.5}. Zatem pod wpływem momentu siły M określonego równaniem (10.1) kąt y wychylenia z położenia równowagi zmięma się periodycznie w taki sposób jak funkcja cosinus (rys. 10.1). W praktyce ozaacza. to, że bryła oscyluje wokół położenia równowagi z częstością kołową Jeżeli przyjmujemy,, że. w chwili początkowej, gdy ( wtedy przesunięcie fazowe = O (rys. 10.1 b) i rozwiązanie równania przyjmie postać
(10.7)
![]()
i
(10.7a)
Funkcja cosinus jest funkcją periodyczną i jej wartości powtarzają się co 2w. Korzystając z powyższej własności i równania (10,7) wyznaczyć możemy okres T, tzn. czas, po którym funkcja cosinus wraca do początkowej wartości
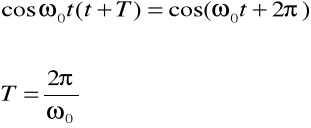
skąd
(10.8)
Podstawiając za Wartość z równania (10.3), otrzymamy
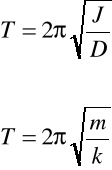
(10.9a)
Wzór powyższy posiada bardzo ważne znaczenie praktyczne, gdyż łączy on okres drgań bryły z jej momentem bezwładności i momentem kierującym. Przy praktycznym korzystaniu z powyższego wzoru należy pamiętać, że wszystkie wielkości muszą być określone względem tej samej osi oscylacji.
11. DRGANIA AKUSTYCZNE
11.01, RÓWNANIE FALI
Na element Δx struny wychylonej z położenia równowagi działają siły F i —F, tworzące z osią x niewielkie kąty α1 i α2 (rys. 11.1). Składowe tych sił w kierunku osi y wynoszą: -Fsinα1 i Fsin2, a wypadkowa w kierunku osi y wynosi F = (sinα2 - sinα1). Wychylenie struny i wartości kątów są nieznaczne, stąd przyjmujemy sinα1= tgα1.
![]()
A to jest równe
i siłę wypadkową wyrażamy wzorem
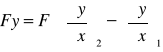
11.1. Odcinek wychylonej struny.
![]()
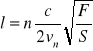
![]()
![]()
![]()
![]()
![]()
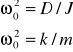
![]()
![]()
![]()
![]()
![]()
![]()
![]()
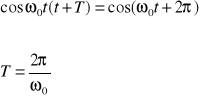
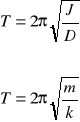
10.9
![]()
10.1. Drgania harmoniczne proste.
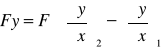
Wyszukiwarka
Podobne podstrony:
warto ci aib do drga struny, Księgozbiór, Studia, Fizyka
Drgania harmoniczne struny, Księgozbiór, Studia, Fizyka
Analiza spr, Księgozbiór, Studia, Fizyka
06 Badanie zaleznosci sily, Księgozbiór, Studia, Fizyka
metoda Bragga, Księgozbiór, Studia, Fizyka
Kopia cechowanie termopary, Księgozbiór, Studia, Fizyka, Biofizyka
Drgania har. -Aga, Księgozbiór, Studia, Fizyka
Analiza ruchu prostolinioweg1, Księgozbiór, Studia, Mechnika Doświadczalna, Zwykła
Wyznaczanie energii maksymalnej promieniowania beta, Księgozbiór, Studia, Fizyka
IS1, Księgozbiór, Studia, Fizyka
LABFIZ08, Księgozbiór, Studia, Fizyka
bragg, Księgozbiór, Studia, Fizyka
Kopia hematokryt, Księgozbiór, Studia, Fizyka, Biofizyka
więcej podobnych podstron