Charakterystyki składu granulometrycznego

W opracowywaniu zależności opisujących poszczególne parametry równania krzywej wodnej retencyjności (np. w mozdelu Coreya-Broksa lub Van Genuchtena) stosowane są różnorodne parametry składu granulometrycznego gleb. Stosowane są zarówno tradycyjne cząstkowe zawartości poszczególnych frakcji (Vereecken i in. 1989, Schaap i in. 2001) oraz wskaźniki ziarnistości, takie jak średnia geometryczna wielkość ziaren dg (Scheinost i in. 1997; ENR 6 Miniasny i in. 1999; Miniasny i McBratney 2001). W analizach tych wykorzystywane są również parametry równania opisującego dystrybuantę uziarnienia gleb (Heverkamp i in. 1997) oraz miary fraktalne cząstek glebowych (Miniasny i McBratney 2000).

Informacja na temat uziarnienia gleb ograniczona jest często do udziału 3 podstawowych frakcji piaskowej, pyłowej i iłowej, informacja o udziale części szkieletowych jest już rzadziej dostępna (Batjes 2002). Dla tak uproszczonego opisu uziarnienia gleb Shirasi i Boersma (1984), a następnie Shirasi i in. (1988) zaproponowali wyznaczenie średniej geometrycznej wielkości cząstek dg i jej odchylenia standardowego σg:

dg = exp(a) (57)

σg = exp(b) (58)

a = (f_sz × ln(M_sz)) + Σ((1-f_sz) × f_i × ln(M_i)) (59)

b² = (f_sz ×ln(M_sz)² + Σ((1-f_sz) × f_i ×ln(M_i)²))- a² (60)

gdzie: f_sz - cząstkowa zawartość części szkieletowych (>2 mm) (-)

f_i - cząstkowy udział i-tej frakcji w częściach ziemistych (<2 mm) (-)

ln(M_i) - średnia logarytmów: górnej i dolnej granicy przedziału wielkości cząstek dla danej frakcji.

W obliczeniach parametrów dg i σg Shirasi i in. (1988) wprowadzili cztery frakcje granulometryczne tj. iłową (0 - 0,002 mm), pyłową (0,002 - 0,05 mm), piaskową (0,05 - 2 mm) oraz części szkieletowe (2 - 75 mm). Dolna granica wielkości cząstek przyjęta została w w zakresie 0,00001 ÷ 0,00005 mm. Scheinost i in. (1997) w obliczeniach wielkości dg i σg przyjęli górną granicę wielkości cząstek równą 63 mm, a dolną 0,00004 mm.

W modelowaniu KWR i współczynnika filtracjii stosowane są także charakterystyki uziarnienia wyznaczone na bazie teorii fraktali. Teorię fraktali do oszacowania fraktalnej wielkości cząstek glebowych zaadoptowali Tyler i Wheatcraft (1989, D₁), po czym Tyler i Wheatcraft (1992) oraz Chang i Uehara (1994) zaproponowali kolejny sposób wyznaczania wielkości fraktalnej cząstek (D₂). Na bazie tego zapisu Bui i in. (1996), przyjmując 2 μm i 2000 μm odpowiednio za dolną i górną wielkości cząstek, opracowali zależność między rozmiarem fraktalnym D2 i zawartością frakcji iłowej (0 < D₂ < 3):

D₂= 0,1448 ln (%Iłu) + 2,333 (61)

Kolejną interpretację rozmiaru fraktalnego (D₃) przedstawili Kravchenko i Zhang (1998)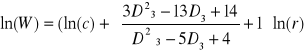
(62)

Oceniając przydatność powyższych modeli fraktalnych Miniasty i McBaratney (2000) stwierdzili, iż do modelowania właściwości hydraulicznych najbardziej przydatna jest wielkość D₂ obliczona według równania Bui i in. (1996; tutaj równanie 61).

Kolejny sposób interpretacji rozmiaru fraktalnego przedstawili ostatnio Perrier i Bird (2002, rys. 28):

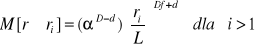
(62)

gdzie: M - masa cząstek o średnicy mniejszej od r_i; d - liczbą wymiarów przestrzeni Euklidesowej (d =2 w przestrzeni dwuwymiarowej i d=3 w przestrzeni trójwymiarowej), L- rozmiar zależny od skali fragmentacji, D- wymiar fraktalnej granicy między cząstkami i porami (D≅d). Wielkość D_f jest oszacowywana na podstawie nachylenia lnM i lnr_i.

Df +3 = 0,88 → Df = 2,12

Rys. 28. Interpretacja wymiaru fraktalnego według Perrier i Bird (2002).

Teoria fraktali była także stosowana do opisu krzywej wodnej retencyjności - pierwszym takim modelem było zasadzie równanie Brooks-Coreya (1964). Fraktalny zapis KWR przedstawili Rieu i Sposito (1991),

W ostatnim czasie w modelowaniu hydraulicznych właściwości gleb Martin i in. (2005a) zastosowali zrównoważony wskaźnik entropii BEI (balanced entopy index; Martin i in. 2005b, Rey i i. 2006), a wielkość ta okazała się najlepszym pojedynczym estymatorem wilgotności gleby przy potencjale -33kPa.

Zrównoważony wskaźnik entropii BEI stanowi przeskalowany wskaźnik entropii H Shannona (Shannon 1948a, b) zgodnie z równaniem Martina i in. (2005b):

(63)

(64)

gdzie: d(P_i║r_i) jest wymiarem Kullbacka-Leiblera (1951), według Covera i Thomasa (1991) wyrażony równaniem:

(65)

n - ilość frakcji (i=3 dla podziału na frakcje piaskową, pyłową i iłową),

P_i - cząstkowy udział i-tej frakcji (ułamek),

r_i - stosunek zakresu średnic frakcji I_i do zakresu średnic części ziemistych I=2 (mm), gdzie r₁ + r₂ + r₃ = 1; dla frakcji piaskowej r₁ = 0,975, pyłowej r₂ = 0,024 oraz iłowej r₃ = 0,001.

Dla schematu podziału na n frakcji w obrębie części ziemistych zrównoważony wskaźnik entropii BEI Martina i in. (2005b) zapisać można równaniem :

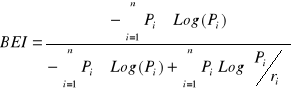
(66)

lub w równoważnym zapisem:

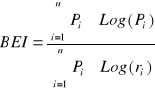
(67)

Rys. 29 Zróżnicowanie wartości wskaźnika BEI w międzynarodowym systemie podziału na frakcje granulometryczne (Rey i in. 2006).

Zrównoważony wskaźnik entropii BEI (Martin i in. 2005b) wydaje się być istotną miarą niejednorodności uziarnienia gleb, a rozkład jego wartości na tle zawartości frakcji piaskowej i iłowej według Rey i in. (2006) przedstawiono rys. 29.

wartości BEI

Udział frakcji iłowej (<0,002 mm)

Udział frakcji piaskowej (2-0,05 mm)

---