Wprowadzenie
Substancja rozpuszczona w dwu pozostających w równowadze ze sobą fazach (np. dwie nie mieszające się ze sobą ciecze, gaz i ciecz itp.) ulega rozdziałowi pomiędzy te fazy. W określonej temperaturze stosunek stężeń tej substancji w obydwu fazach jest wielkością stałą. Jest to podane przez Nernsta tak zwane prawo podziału.
Oznaczając przez cI oraz cII stężenia rozpuszczonej substancji w fazach I i II, można napisać:
![]()
. (1)
Stała r nosi nazwą współczynnika podziału. Prawo podziału Nernsta stosuje się w tej formie w roztworach rozcieńczonych w przypadku, gdy stan cząsteczkowy substancji rozpuszczonej jest jednakowy w obydwu fazach.
Rozpatrzmy obecnie przypadek substancji, która w jednej z faz ulega silnej asocjacji, w drugiej zaś pozostaje głownie w stanie zdysocjowanym (przez dysocjację rozumiemy proces odwrotny do asocjacji). Równowagi te ilustruje schemat:
W każdej z faz ustala się równowaga asocjacyjno-dysocjacyjna (nie należy mylić tego procesu z dysocjacją elektrolityczną). Zakładając w fazie I silne przesunięcie równowagi w kierunku asocjacji (np. stopień dysocjacji I = 0.01) oraz w kierunku dysocjacji w fazie II (np. II = 0.99) można napisać w przybliżeniu:
![]()
,
gdzie cI oraz cII oznaczają analitycznie określone stężenia substancji, bez uwzględnienia asocjacji czy dysocjacji. Przesunięcie równowagi zaznaczono w schemacie pogrubionymi strzałkami.
Stany równowagi w poszczególnych fazach charakteryzują odpowiednie stałe:
![]()
(2)
i
![]()
. (3)
Gdy substancja rozpuszczona ulega częściowej dysocjacji lub asocjacji, prawo podziału zachowuje ważność dla ułamka substancji występującej w tym stanie cząstkowym w obydwu fazach. Biorąc to pod uwagę, można napisać:
![]()
. (4)
Dążymy do zastąpienia w równaniu (4) trudnej do wyznaczenia doświadczalnego wartości cA,I - w fazie I równowaga jest przesunięta w kierunku An - przez łatwą do analitycznego wyznaczenia wartości cI.
W tym celu przekształca się równanie (2):
![]()
. (5)
Wstawiając równanie (5) do (4) otrzymuje się:
![]()
, (6)
lub w dogodniejszej dla doświadczalnego sprawdzenia postaci:
![]()
. (7)
Cel ćwiczenia
Tematem ćwiczenia jest wyznaczenie współczynnika podziału kwasu benzoesowego C6H5COOH pomiędzy wodę i benzen oraz sprawdzenie, czy w obydwu fazach kwas benzoesowy występuje w tym samym stanie cząsteczkowym. W przypadku stwierdzenia różnic stanu drobinowego należy próbować wyznaczyć, w oparciu o uzyskane wyniki, ilość drobin asocjujących.
Opracowanie wyników
Vr.wodnego [ml] |
Vr.butanolowego [ml] |
Vpróbki [ml] |
Stężenie NaOH [m/l] |
Temperatura [oC] |
||
25.0 |
25.0 |
5.0 |
0.1 |
24.0 |
||
Nr próbki |
Co kwasu |
VNaOH |
Cr.wodnego |
Cbutanolu |
r |
|
|
[m/l] |
[ml] |
[m/l] |
[m/l] |
|
|
1 |
1.00 |
22.8 |
22.7 |
0.454 |
0.546 |
0.832 |
|
|
22.6 |
|
|
|
|
2 |
0.75 |
17.0 |
17.0 |
0.340 |
0.410 |
0.829 |
|
|
17.0 |
|
|
|
|
3 |
0.50 |
11.4 |
11.35 |
0.227 |
0.273 |
0.832 |
|
|
11.3 |
|
|
|
|
4 |
0.25 |
5.8 |
5.8 |
0.116 |
0.134 |
0.866 |
|
|
5.8 |
|
|
|
|
5 |
0.10 |
2.4 |
2.4 |
0.048 |
0.052 |
0.923 |
|
|
2.4 |
|
|
|
|
6 |
0.05 |
1.2 |
1.2 |
0.024 |
0.026 |
0.923 |
|
|
1.2 |
|
|
|
|
![]()
![]()
![]()
Z wykreślonej zależności otrzymujemy:
![]()
y = 0.822x + 0.0041
K = 0.0041
n = 1.22 = 1 cząsteczka
Obliczenia dla wyników Nersta
|
|
|
|
|
||
|
|
|
|
|
|
|
1.336 |
0.163 |
-2.874 |
4.385 |
0.535 |
-2.358 |
0.305 |
2.000 |
0.244 |
-2.699 |
8.115 |
0.990 |
-2.091 |
0.246 |
3.705 |
0.452 |
-2.431 |
22.377 |
2.730 |
-1.650 |
0.166 |
6.459 |
0.788 |
-2.190 |
60.410 |
7.370 |
-1.219 |
0.107 |
12.295 |
1.500 |
-1.910 |
198.361 |
24.20 |
-0.703 |
0.062 |
23.389 |
2.890 |
-1.631 |
795.082 |
97.00 |
-0.100 |
0.030 |
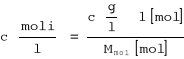
![]()
y = 0.552x - 1.542
K = 0.029
n = 1.81 = 2 cząsteczki
Obliczenia dla wyników Smitha
|
|
|
|
|
||
|
|
|
|
|
|
|
0.8725 |
0.106 |
-3.059 |
1.525 |
0.186 |
-2.817 |
0.572 |
0.925 |
0.113 |
-3.034 |
1.950 |
0.238 |
-2.710 |
0.474 |
1.300 |
0.157 |
-2.886 |
3.450 |
0.421 |
-2.462 |
0.377 |
1.725 |
0.210 |
-2.763 |
5.500 |
0.671 |
-2.260 |
0.314 |
2.800 |
0.342 |
-2.553 |
11.90 |
1.452 |
-1.924 |
0.235 |
4.000 |
0.488 |
-2.398 |
19.75 |
2.410 |
-1.704 |
0.203 |
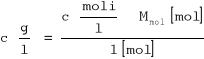
y = 0.604x - 1.3853
K = 0.041
n = 1.656 = 2 cząsteczki
Z wykreślonej zależności otrzymujemy
![]()
y = 0.9586x - 0.0965
K = 0.8
n = 1 cząsteczka
Obliczenia dla wyników Nersta
|
|
|
|
|
||
|
|
|
|
|
|
|
1.336 |
0.163 |
-2.874 |
4.385 |
0.535 |
-2.358 |
0.305 |
2.000 |
0.244 |
-2.699 |
8.115 |
0.990 |
-2.091 |
0.246 |
3.705 |
0.452 |
-2.431 |
22.377 |
2.730 |
-1.650 |
0.166 |
6.459 |
0.788 |
-2.190 |
60.410 |
7.370 |
-1.219 |
0.107 |
12.295 |
1.500 |
-1.910 |
198.361 |
24.20 |
-0.703 |
0.062 |
23.389 |
2.890 |
-1.631 |
795.082 |
97.00 |
-0.100 |
0.030 |
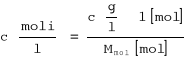
![]()
y = 0.552x - 1.542
K = 0.029
n = 1.81 = 2 cząsteczki
Obliczenia dla wyników Smitha
|
|
|
|
|
||
|
|
|
|
|
|
|
0.8725 |
0.106 |
-3.059 |
1.525 |
0.186 |
-2.817 |
0.572 |
0.925 |
0.113 |
-3.034 |
1.950 |
0.238 |
-2.710 |
0.474 |
1.300 |
0.157 |
-2.886 |
3.450 |
0.421 |
-2.462 |
0.377 |
1.725 |
0.210 |
-2.763 |
5.500 |
0.671 |
-2.260 |
0.314 |
2.800 |
0.342 |
-2.553 |
11.90 |
1.452 |
-1.924 |
0.235 |
4.000 |
0.488 |
-2.398 |
19.75 |
2.410 |
-1.704 |
0.203 |
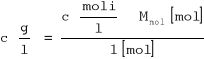
y = 0.604x - 1.3853
K = 0.041
n = 1.656 = 2 cząsteczki
Wnioski
Po obliczeniach i wykreślonych zależnościach można zauważyć, iż współczynnik podziału jest uzależniony od substancji i temperatury.
Otrzymany średni współczynnik podziału kwasu octowego między wodą i alkohol butylowy wynosi 0,8675, a liczba n jest równa 1. W pomiarach Nersta i Smitha wynosi ona 2. Jest to liczba cząsteczek kompleksu (C6H5COOH)n. Współczynnik równowagi dla kwasu octowego wynosi 0.0041, a dla benzenu 0.041 i 0.029.
Po wykreśleniu charakterystyk można stwierdzić, iż wzór ![]()
opisuje zadowalająco zależność stężeń benzenu w obu fazach oraz liczby cząsteczek w kompleksie.
Faza II
Faza I
n
n
n
n
A
A
A
A
Wyszukiwarka
Podobne podstrony:
Pojęcia na egzamin z metali, Chemia Fizyczna, chemia fizyczna- laborki rozne, Rozne
Chemia a ochrona środowiska - referat, Chemia Fizyczna, chemia fizyczna- laborki rozne, Rozne
Katalizatory - referat, Chemia Fizyczna, chemia fizyczna- laborki rozne, Rozne
Ogniwagal.wzor, Chemia Fizyczna, chemia fizyczna- laborki rozne, Ogniwa
wielkości molowe-odp na pytania, Chemia Fizyczna, chemia fizyczna- laborki rozne, Rozne
Ściąga z chemii (Na, Chemia Fizyczna, chemia fizyczna- laborki rozne, Rozne
Ściąga na zaliczenie laboratorium u mgr. Pacławskiego, Chemia Fizyczna, chemia fizyczna- laborki roz
Grupy główne i podgrupy układu okresowego pierwiastków, Chemia Fizyczna, chemia fizyczna- laborki ro
Ściąga do metali z hutnictwa i nie tylko, Chemia Fizyczna, chemia fizyczna- laborki rozne, Rozne
Wodorotlenosole, Chemia Fizyczna, chemia fizyczna- laborki rozne, Rozne
ogniwa chemiczne, Chemia Fizyczna, chemia fizyczna- laborki rozne, Ogniwa
Napięcie powierzchniowe1, Chemia Fizyczna, chemia fizyczna- laborki rozne, NAPIĘCIE POWIERZCHNIOWE
elektrolity, Chemia Fizyczna, chemia fizyczna- laborki rozne, Rozne
Ściąga z chemii (C, Chemia Fizyczna, chemia fizyczna- laborki rozne, Rozne
Liczby przenoszenia, Chemia Fizyczna, chemia fizyczna- laborki rozne, Liczby przenoszenia
okładka-sb lab 15, Chemia Fizyczna, chemia fizyczna- laborki rozne, Rozne
oddana, Chemia Fizyczna, chemia fizyczna- laborki rozne, pH
!!!!!!!!destylacja, Chemia Fizyczna, chemia fizyczna- laborki rozne, destylacja
więcej podobnych podstron