Dodatek A

1. Obliczenie ilości par powierzchni trących i wymiarów płytek.

a. Nacisk powierzchniowy wyraża się stosunkiem

p = Q/F ,

gdzie:

Q - siła docisku ,

F = π (r_z² - r_w²) - powierzchnia docisku.

Natomiast moment tarcia wynosi :

M_T = z Q μ r_śr

gdzie:

z - ilość par powierzchni trących,

μ - współczynnik tarcia,

r_śr - średni promień .

Podstawiając Q = p F mamy

M_T= z p F μ r_śr ,

a po przekształceniu otrzymujemy wzór

.

Ilość płytek zewnętrznych wynosi:

z_z = z/2

Natomiast ilość płytek wewnętrznych

z_w = z_z + 1

b. Obliczenie promienia średniego

Nawiązując do rysunku A.1 moment tarcia na powierzchni elementarnego pierścienia wynosi

dM = p dF μ r ,

gdzie : dF = 2 π r dr

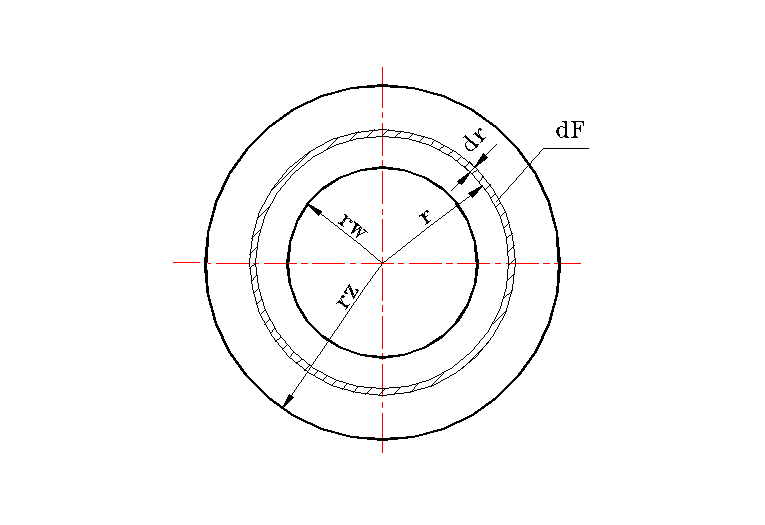
Rys. A.1. Schemat obciążenia powierzchni ciernej

Po podstawieniu otrzymujemy

dM = 2 p π r² μ dr .

Całkowity moment tarcia wynosi:

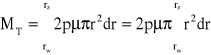
Porównując M_T = Q μ r_śr i podstawiając Q = π p (r_z²-r_w²)

Otrzymamy wzór na promień średni :

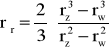
2. Współczynnik przeciążenia sprzęgła

a. Współczynnik przeciążenia bez obciążenia momentem oporu

Miejsce usytuowania sprzęgła pokazuje rys.A.2 , natomiast wykresy momentów i prędkości kątowej przedstawiono na rys. A.3.

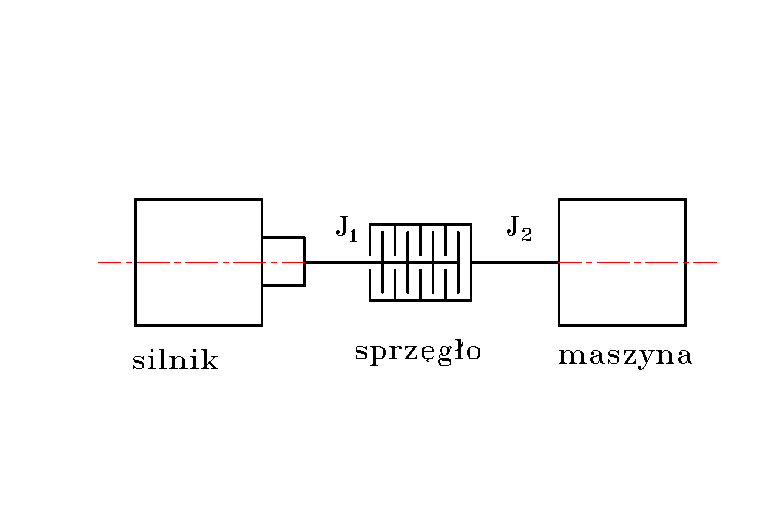
Rys. A.2. Usytuowanie sprzęgła

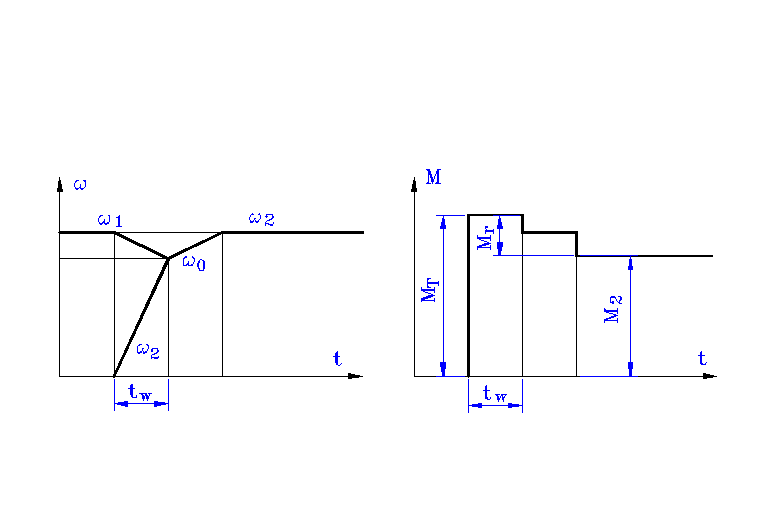
Rys. A.3. Wykresy momentu obrotowego i prędkości kątowej podczas rozruchu sprzęgła

Jeśli moment oporu M₂ = 0, to przyspieszenie kątowe

,

gdzie:

M₁ [Nmm] - maksymalny moment skręcający silnika,

J₁ [kg mm²] - moment bezwładności wirujących mas przed sprzęgłem, zredukowanych

na oś sprzęgła od strony silnika,

J₂ [kg mm²] - moment bezwładności mas napędzanych na wale za sprzęgłem.

Natomiast największy moment obrotowy na sprzęgle wynosi:

Mnożąc stronami powyższe równanie przez moment nominalny M otrzymamy

Wprowadzając symbol k

,

Możemy zapisać

M_o = k * M

Przy wprowadzeniu m = J₁/J₂ współczynnik wynosi:

.

b. Współczynnik przeciążenia, w przypadku gdy M₂ > 0.

W tym przypadku różnica M1 - M2 powoduje przyspieszenie ruchu obrotowego wału napędzanego. Wobec tego moment przenoszony przez sprzęgło wyraża się następująco:

.

Natomiast M_o = M_s * k' ,

gdzie

.

Przy wprowadzeniu m = J₁ / J₂ współczynnik wynosi

.

3. Moment rozruchowy sprzęgła

a. Moment rozruchowy sprzęgła dla M₂ > 0

Zgodnie z zasadą d'Alamberta piszemy zależność

M₁= (J₁ + J₂) ε + M₂

Po przekształceniu powyższego wzoru

.

Natomiast moment rozruchowy wynosi:

.

b. Moment rozruchowy sprzęgła dla M2 = 0

,

Wówczas

.

Dla ruchu jednostajnie przyspieszonego

,

wobec tego

.

Chcąc uzyskać mały moment M_r należy stosować silnik o małym nadmiarze momentu (ΔM=M₁-M₂), sprzęgło umieścić jak najbliżej maszyny roboczej (małe J₂₎, włączać sprzęgło na biegu jałowym maszyny (M₂=0).

c. Przenoszony moment rzeczywisty

Aby sprzęgło przenosiło moment rzeczywisty bez poślizgu, musi być tak wyregulowane, aby rzeczywisty moment przenoszony znajdował się zawsze poniżej momentu tarcia sprzęgła M_T (rys.A.4a). Przykładowo na rys. A.4b przedstawiono sprzęgło źle wyregulowane, gdzie zmienny moment rzeczywisty przekracza moment tarcia i następuje okresowe ślizganie się sprzęgła, co jest niedopuszczalne podczas dłuższej pracy (ze względu na wzrost temperatury sprzęgła i nierównomierną pracę maszyny roboczej).

d. Tłumienie występujące w sprzęgle

W sprzęgłach swobodnych następuje łagodzenie uderzenia sprzęgła przez zmianę pracy uderzenia na pracę sprężystego odkształcenia. Złagodzenie uderzenia oznaczono jako A na rys.A.5, natomiast w sprzęgłach tłumiących możliwe jest całkowite zlikwidowanie uderzenia , co przedstawia rys. A.6.

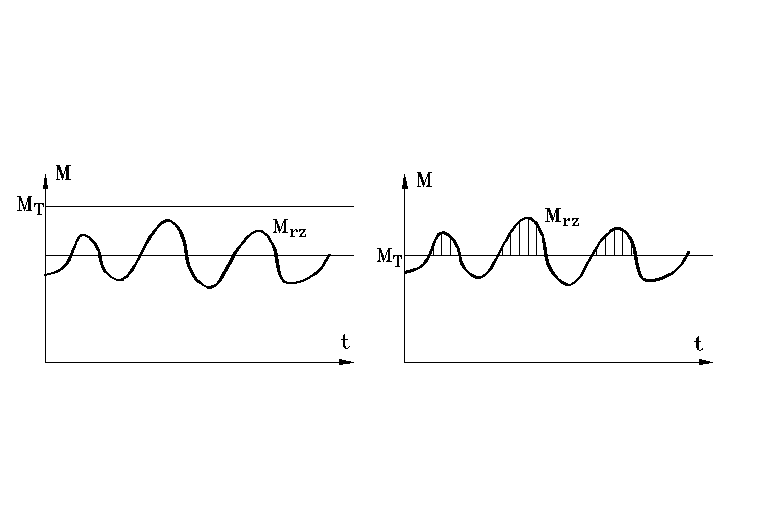
Rys.A.4. a) przebieg rzeczywistego momentu tarcia dla sprzęgła dobrze wyregulowanego

b) zależność momentu rzeczywistego dla sprzęgła źle wyregulowanego

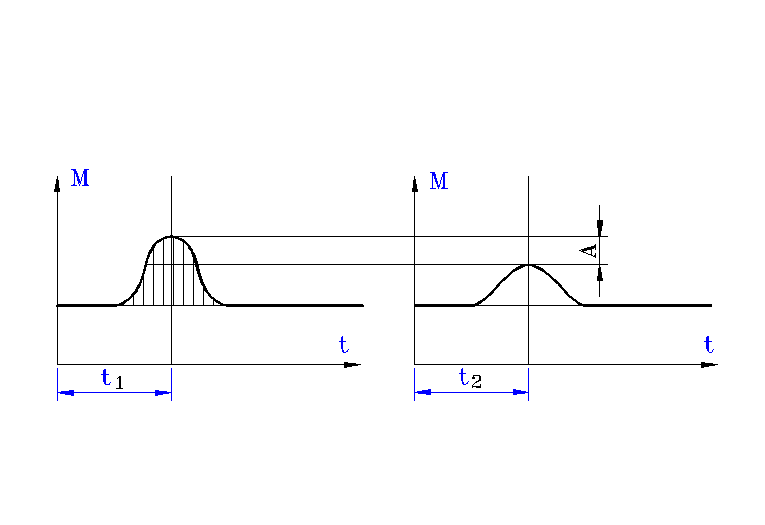
Rys. A.5. Przebieg łagodzenia uderzenia na sprzęgle

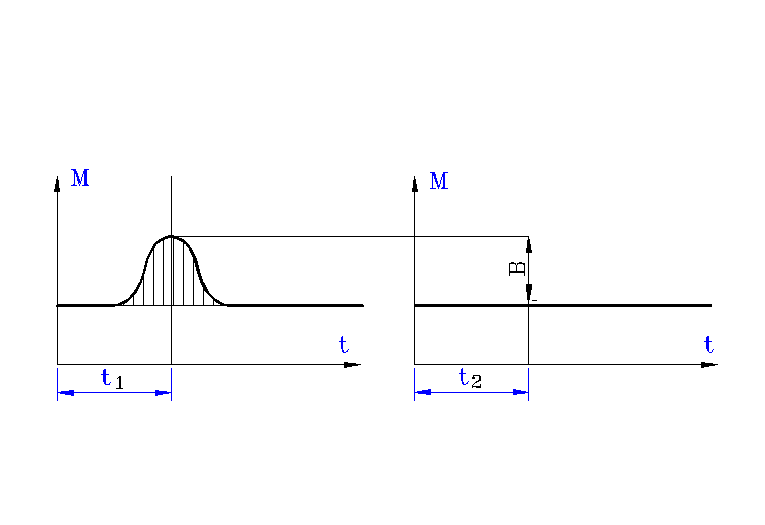
Rys. A.6. Zlikwidowanie uderzenia na sprzęgle

Silne tłumienie można osiągnąć przez zastosowanie elementów podatnych z materiałów o dużym współczynniku tłumienia Ψ. Współczynnik ten jest wyrażony stosunkiem pracy rozproszonej do pracy włożonej, przy odkształceniu sprężystym.

Znaczny wpływ ma zabezpieczenie przed przeciążeniem przypadkowym ma odpowiednia sztywność mechanizmu włączania. W niektórych konstrukcjach sprzęgieł istnieją specjalne elementy sprężyste, mające za zadanie umożliwienie poślizgu przy chwilowym przekroczeniu momentu tarcia. Elementy te dodatkowo powodują bardzo łagodny rozruch.

4. Straty tarcia w sprzęgle ciernym

a. Straty tarcia sprzęgła przy włączaniu na biegu luzem maszyny.

Przy założeniu M₁ = const i ω₁ = const, natomiast ω₂=0 (wał nieruchomy). Podczas rozruchu ω₂ = ω < ω₁ . Moment skręcający silnika wobec strat tarcia i poślizgu wynosi

.

Energia dostarczona przez silnik w czasie rozruchu jest następująca:

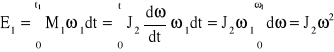
Energia uzyskana przez masy wirujące, związane z wałem napędzanym dla ω = ω₁ , wynosi

.

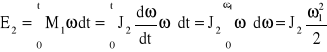
A zatem energia stracona na tarcie w sprzęgle ciernym przy przyspieszaniu mas bezwładności wynosi:

E_T = E₁ - E₂ = E₁/2

Jak wynika ze wzoru na E_T energia zamieniona na tarcie w sprzęgle stanowi zawsze połowę energii dostarczonej przez silnik w czasie t_w (rys.A.2).

b. Straty tarcia sprzęgła przy włączaniu pod obciążeniem

Rozważmy przypadek, gdy M1 ≠ const i M2 ≠ 0.

Gdy M1 < M2, silnik nie napędza wału napędzanego i cała energia dostarczona w tym czasie zostaje zamieniona na tarcie (stracona):

.

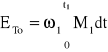
W momencie, gdy M₁ > M₂, zaczyna być wprawiany w obrót wał pędzony z przyspieszeniem

,

a strata tarcia przy przyspieszaniu mas bezwładności na wale pędzonym wynosi:

.

Występuje również strata tarcia przy pokonywaniu momentu M₂, którą możemy obliczyć jako różnicę pracy dostarczonej i odebranej

E_T2 = E_d - E_o ,

gdzie:

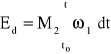
- praca dostarczona przez silnik na pokonanie M₂ ,

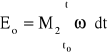
- praca odebrana przez wał napędzany,

a zatem

.

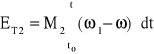
Natomiast całkowita strata tarcia w sprzęgle przy tym sposobie włączania wynosi

E_T = E_T0 + E_T1 + E_T2 .

Po podstawieniu wzór przedstawia się następująco:

.

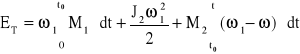
Wnioski.

Aby zmniejszyć straty tarcia przy rozruchu należy:

1. włączać sprzęgło przy M₁ > M₂, wówczas E_T0 = 0,

2. włączać sprzęgło przy małych oporach zewnętrznych (małe M₂) i w krótkim czasie (małe t_w),

3. włączać sprzęgło bez szarpnięć, zwiększając płynnie siłę nacisku na powierzchniach ciernych (poprzez elementy sprężyste).

Zalecany czas włączania sprzęgła ciernego wynosi t < 1 ÷ 2 s, dla sprzęgieł obrabiarkowych t<0,2 ÷ 0,3 s, w automatach t ≈ 0,05 s. Przy wyłączaniu powstają również straty tarcia, lecz małe w porównaniu ze stratami przy włączaniu, że nie mają praktycznie znaczenia.

5. Określenie zastępczego momentu bezwładności wirujących mas układu

1. Jeśli pominiemy straty tarcia w mechanizmie, to momenty bezwładności wirujących mas wyniosą J₁, J₂, J₃, J_n. Natomiast wywołane przyspieszenia lub opóźnienia kątowe dowolnego członu spowodują przyspieszenie lub opóźnienie członów związanych przełożeniem.

Na każdym członie pojawi się moment dynamiczny o wartości M₁, M₂, M₃, M_n. Redukując poszczególne momenty na wał silnika otrzymamy:

.

W mechanizmie rzeczywistym, uwzględniając powstające straty w przypadku rozruchu przy przepływie strumienia mocy od członu 1 do pozostałych, otrzymamy równanie

.

W celu nadania przyspieszenia lub opóźnienia należy przyłożyć następującą wartość momentu:

.

Uwzględniając związki:

, itd., otrzymujemy

.

Po podstawieniu zastępczy moment bezwładności wirujących mas zredukowanych na wał silnika przy rozruchu wyraża się zależnością

.

6. Nagrzewanie się sprzęgła

Nagrzewanie jest dopuszczalne tylko do pewnej temperatury. Dla materiałów ciernych po przekroczeniu tej temperatury następuje zmiana współczynnika tarcia i szybki wzrost zużycia spowodowane rozhartowaniem płytek ciernych. Wykresy przebiegu nagrzewania i stygnięcia sprzęgła zostały przedstawione na rys. A.7. Krzywa nagrzewania i stygnięcia są krzywymi wykładniczymi. Dla stałej mocy tarcia i prędkości obrotowej zależności przedstawiono na rys. A.7 jako krzywe a i b. Natomiast zależności stygnięcia przedstawia krzywa c.

Przy ciągłym włączaniu i wyłączaniu wykres będzie miał kształt składający się z odcinków nagrzewania i stygnięcia. Nadwyżka temperatury Δt_max osiąga swe maksimum po długim czasie pracy (nawet po kilku godzinach).

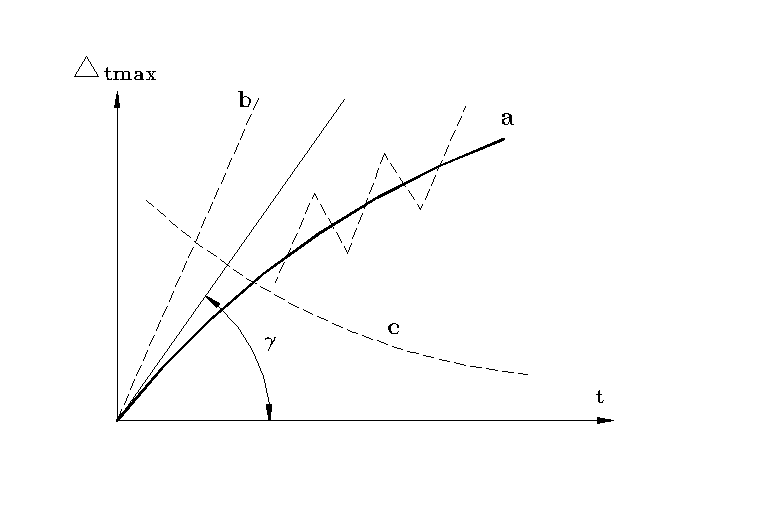
Rys.A.7. Przebieg nagrzewania i stygnięcia sprzęgła

a,b, - krzywe nagrzewania, c - krzywa stygnięcia

Nadwyżkę temperatury Δt_max obliczamy z przeciętnej godzinowej pracy tarcia

gdzie:

L_T=0.5 L_r [Nm] - praca tarcia przy jednym włączeniu,

L_r= M_T*J₂*ω²/M_r - praca w czasie rozruchu

w - ilość włączeń w ciągu godziny,

F [m²] - powierzchnia odprowadzająca ciepło,

α [W/(m²*^oC)] - współczynnik odprowadzenia (wnikania) ciepła.

Przy naturalnym chłodzeniu powietrzem można przyjąć :

α=5,23+6,98*v^3/4

a przy zmiennych czasach włączania i prędkościach obrotowych

,

gdzie:

α₁ , α₂ - obliczone dla odpowiednich prędkości obrotowych,

t_w1, t_w2 - czasy włączania.

Wobec powyższego temperaturę sprzęgła wyraża wzór

t_s = t_p +Δt_max ≤ t_dop ,

gdzie:

t_p [^oC] - temperatura otaczającego powietrza,

t_dop [^oC] - temperatura dopuszczalna.

Dane te podane są w tablicy A.1. Należy pamiętać, że temperatura na powierzchniach ciernych jest wyższa. Dla sprzęgieł wielopłytkowych stosuje się dotychczas najbardziej ogólne sprawdzenie na grzanie sprzęgła, a mianowicie:

p_rz * v ≤ N_i

co jest dokładniej opisane w toku obliczeń sprzęgła wielopłytkowego.

7. Trwałość powierzchni ciernych sprzęgła

Ilość godzin pracy powierzchni ciernych sprzęgła wynosi:

gdzie:

V_z [mm³] - dopuszczalne objętościowe zużycie powierzchni ciernych,

q_v [mm³/kWh] - zużycie właściwe płytek, zależne od materiału, smarowania, prędkości i

temperatury (wartości podane w tablicy A.2)

N_T [W] - średnia moc tarcia (przypadająca np. na 1 sekundę ),

.

Zużycie objętościowe można przedstawić następująco:

V_s = F * s_z ,

gdzie:

F [mm²] - powierzchnia cierna jednej płytki,

s_z [mm] - dopuszczalne liniowe zużycie okładzin ciernych.

Dla okładzin ciernych s_z =(0,8÷0,9)g, przy oznaczeniu g jako grubości okładziny. Dla płytek stalowych i żeliwnych s_z = (0,1 ÷ 0,2) g .

8. Dopuszczalny nacisk powierzchniowy

Wielkość dopuszczalnego nacisku jednostkowego została przedstawiona przez zależność

p = p_o c_v c_i c_z [MPa] ,

gdzie

p_o [MPa] - dopuszczalny nacisk jednostkowy na powierzchni styku w idealnych warunkach

pracy sprzęgła,

- współczynnik prędkości poślizgu,

v [m/s] - średnia prędkość obwodowa.

c_i - współczynnik liczby przełączeń , obliczany z wzoru:

c_i = 1 - 0,002 (w-90) ≤ 1 ,

gdzie : w= 90 ÷ 360 włączeń na godzinę .

c_z - współczynnik zależny od liczby powierzchni trących.

Zależność wartości c_z w funkcji ilości par powierzchni trących podaje tablica A.5.

Tablica A.5

z	1÷3	4	5	6	7	8	9	10	11
cz	1,0	0,97	0,94	0,91	0,88	0,85	0,82	0,79	0,76

Sprzęgła mokre stosuje się normalnie dla n ≤ 1000 do 1800 obr./min. Sprzęgła suche normalnie dla n ≤ 1200 obr./min, max. do n ≤ 4000 obr./min.

Wielkość stosowanych rozsunięć tarcz przedstawia się następująco:

δ = 0,2 ÷ 0,5 [mm] - dla sprzęgła wielopłytkowego z metalowymi tarczami,

δ = 0,5 ÷ 1,0 [mm] - dla sprzęgła jednotarczowego z metalową tarczą oraz dla sprzęgieł wielopłytkowych z okładzinami ciernymi niemetalowymi,

δ = 0,8 ÷ 1,5 [mm] - dla sprzęgła jednotarczowego z niemetalowymi okładzinami ciernymi.

Maksymalne wartości siły sterującej P [N] oraz drogi u [mm] i pracy L[Nmm] wynoszą:

L = P*u = Q *δ* z .

Dla sterowania ręcznego:

P = 150 ÷ 200 N, u = 40 ÷ 75 [mm] , L=75000 [Nmm] .

Natomiast dla sterowania nożnego

P = 200 ÷ 300 N, u = 18 ÷ 25 [mm] , L=30000 [Nmm] .

Sprawność mechaniczna mechanizmu włączania wynosi:

.

W dużych sprzęgłach siłę ludzką zastępuje się serwomotorem, czyli siłownikiem hydraulicznym, pneumatycznym lub magnetycznym, najczęściej umieszczonym w sprzęgle. Ciśnienie oleju sterującego sięga 2,5 MPa, a w specjalnych rozwiązaniach dochodzi do 12,5 MPa. Z tej racji sprzęgła przełączane hydraulicznie mają mniejsze wymiary i dużą ich zaletą jest możliwość zdalnego sterowania. W sprzęgłach pneumatycznych ciśnienie powietrza wynosi 0,6 do 1 MPa.

21

---