Sprawozdanie z ćwiczenia nr 34.
Michał Tyszko
Marcin Wróblewski
Gdy światło pada na granicę dwóch izotropowych ośrodków materialnych pojawia się fala przechodząca i fala odbita. Fala przechodząca jest falą załamaną. Zjawisko załamania światła to zmiana kierunku rozchodzenia się fali świetlnej (lub zmianie kierunku biegu wiązki światła).
Dyspersją optyczną materiału nazywamy istnienie różnych wartości współczynnika załamania światła n dla różnych częstotliwości fali świetlnej v.
Dyspersja światła jest charakterystyczna dla danego materiału w obszarach widmowych, w których dana substancja jest przezroczysta. Współczynnik załamania zwiększa się wraz ze wzrostem częstotliwości światła. Tam gdzie substancja absorbuje światło dzieje się inaczej - wraz ze wzrostem częstotliwości maleje współczynnik załamania. Zjawisko to nazywamy dyspersją anormalną.
Aby wyznaczyć kąt łamiący pryzmatu ustawiliśmy lunetę na obserwacji wiązki odbitej od jednej ściany pryzmatu i odczytaliśmy położenie lunety "a" stopni, następnie zaobserwowaliśmy obraz promieni odbitych od drugiej ściany i zapisaliśmy położenie "b". Kąt łamiący jest równy połowie różnicy tych odczytów i można go wyznaczyć za pomocą wzoru:
![]()
Prawa Strona (a) |
|
Lewa Strona (b) |
||||
|
Noniusz A |
Noniusz B |
|
|
Noniusz A |
Noniusz B |
Kąt |
|
|
|
Kąt |
|
|
Obliczenia kąta łamiącego wyliczyliśmy następująco:
1. |
|
|
|
2. |
|
|
|
Następnie wyznaczyliśmy szerokość kątową szczeliny,
Noniusz A |
|
Szerokość Kątowa Szczeliny |
Kąt |
Prawa Strona |
|
Lewa Strona |
|
Różnica |
|
aby w rezultacie określić błąd pomiaru kąta łamiącego.
![]()
Aby wyznaczyć kąt najmniejszego odchylenia ![]()
dla poszczególnych linii neonu, najpierw zanotowaliśmy wartości kątów dla poszczególnych barw, a po wykonaniu pomiarów usunęliśmy pryzmat i zanotowaliśmy położenie kolimatora na wprost:
Odczyt Środkowy |
|
Nr |
Barwa |
Noniusz B |
||
|
|
|
kąt |
minuty |
1 |
Czerwony |
|
132 |
56 |
2 |
Pomarańczowy |
|
133 |
20 |
3 |
Pomarańczowy |
|
133 |
30 |
4 |
Pomarańczowy - Żółty |
|
133 |
50 |
5 |
Żółty |
|
134 |
4 |
6 |
Zielony |
|
134 |
34 |
7 |
Zielony |
|
134 |
50 |
8 |
Zielony |
|
135 |
|
9 |
Niebiesko-Zielony |
|
135 |
10 |
10 |
Niebieski |
|
135 |
36 |
11 |
Fioletowy |
|
136 |
30 |
Wartość wyznaczamy ![]()
wg wzoru poniżej i podajemy w radianach:
![]()
odczyt środkowy - kąt łamiący pryzmatu
Nr |
Barwa |
|
1 |
Czerwony |
0,9948 |
2 |
Pomarańczowy |
1,0018 |
3 |
Pomarańczowy |
1,0047 |
4 |
Pomarańczowy - Żółty |
1,0105 |
5 |
Żółty |
1,0146 |
6 |
Zielony |
1,0233 |
7 |
Zielony |
1,0280 |
8 |
Zielony |
1,0309 |
9 |
Niebiesko-Zielony |
1,0338 |
10 |
Niebieski |
1,0414 |
11 |
Fioletowy |
1,0571 |
Błąd ![]()
wyznaczamy przy użyciu różniczki zupełnej:
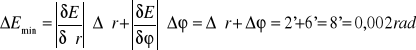
Na podstawie wzoru: 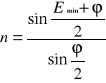
obliczyliśmy współczynniki załamania światła n od długości fali ![]()
dla kolejnych linii. Wyniki zamieściliśmy w tabeli poniżej:
Nr |
Barwa |
n w radianach |
1 |
Czerwony |
1,7055 |
2 |
Pomarańczowy |
1,7092 |
3 |
Pomarańczowy |
1,7107 |
4 |
Pomarańczowy - Żółty |
1,716 |
5 |
Żółty |
1,717 |
6 |
Zielony |
1,7203 |
7 |
Zielony |
1,7226 |
8 |
Zielony |
1,7241 |
9 |
Niebiesko-Zielony |
1,7256 |
10 |
Niebieski |
1,7294 |
11 |
Fioletowy |
1,7373 |
Błąd ![]()
wyznaczyliśmy metodą różniczki zupełnej:

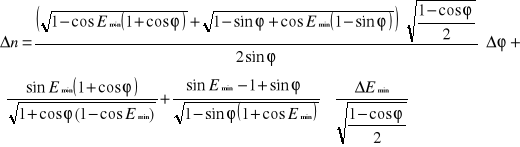
Niepewność jest równa dla wszystkich długości fali i wynosi Δn=0,002.
Z polecenia prowadzącego zamieściliśmy wykres krzywej zależności współczynnika załamania światła n od długości fali ![]()
, czyli tzw. krzywą dyspersji.
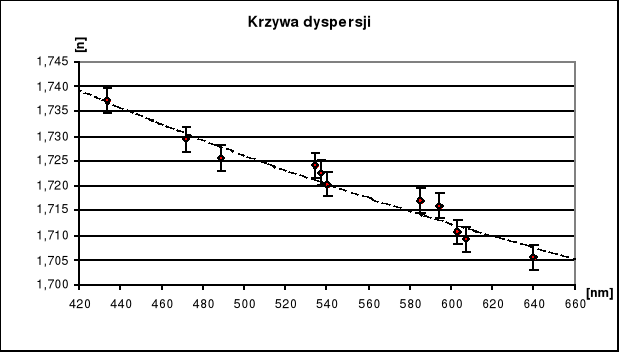
-3-
Wyszukiwarka
Podobne podstrony:
Srodki trwale-wstep, UEP (2014-2017), rachunkowosc
Wykład z rachunkowości 7, UEP (2014-2017), rachunkowosc
Materialy-zadania, UEP (2014-2017), rachunkowosc
PLAN 14 2017
Diody, Politechnika Rzeszowska - Elektronika i telekomunikacja 2012-2017, II rok
2016 05 20 Ustawa Program modernizacji Policji 2017 2020 projekt
1996 10 22 2017
Pytania z wyk adów, UEP (2014-2017), Prawo.WE
Przykładowe pytania na egzamin z fakultetu drożdże termin zerowy, Studia (2012-2017) SGGW - WNoŻ - T
Koszty-zadania, UEP (2014-2017), rachunkowosc
Wykład z rachunkowości 2, UEP (2014-2017), rachunkowosc
Temat 4 i 5 - Konto ksiegowe - rozwiazania zadan, UEP (2014-2017), rachunkowosc
prawo bka, UEP (2014-2017), Prawo.WE
Exam, UEP (2014-2017), rachunkowosc
Produkty pracy-zadania, UEP (2014-2017), rachunkowosc
Wykład z rachunkowości 10, UEP (2014-2017), rachunkowosc
9 - WE - Materialy-konspekt, UEP (2014-2017), rachunkowosc
więcej podobnych podstron