LABORATORIUM FIZYKI 1 |
Ćwiczenie nr: 2 |
|||
Wydział: SiMR |
Grupa: 2.1. |
Zespół: I I |
Data: 28.10.98 |
|
Nazwisko i imię:
|
ocena |
Przygotowanie: |
||
Temat ćwiczenia: Wyznaczanie przyśpieszenia ziemskiego i modułu sprężystości. |
|
Zaliczenie: |
||
I. Wyznaczanie przyśpieszenia ziemskiego za pomocą wahadła fizycznego,
rewersyjnego.
Wartość przyśpieszenia ziemskiego:
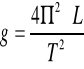
gdzie: L - długość zredukowana wahadła fizycznego ,
T - okres drgań tego wahadła.
Wyznaczanie długości zredukowanej i okresu wahań wahadła fizycznego.
Wartości okresów dla skrajnych położeń ciężarków:
oś A oś B
1. 1,84 1,94
2. 2,23 2,10
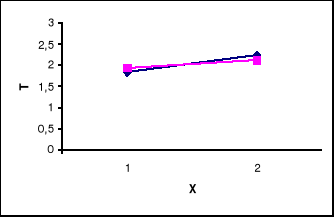
Z powyższego wykresu wynika , że możliwe jest odnalezienie takiego położenia
obciążnika , dla którego dane wahadło fizyczne stanie się wahadłem rewersyjnym.
Wyniki pomiarów okresów wahań w zależności od wyboru osi i położenia
obciążnika.
odl. |
3 |
6 |
9 |
10 |
11 |
12 |
TA |
2,16 |
2,12 |
2,07 |
2,05 |
2,04 |
2,01 |
TB |
2,07 |
2,03 |
2,03 |
2,05 |
2,04 |
2,03 |
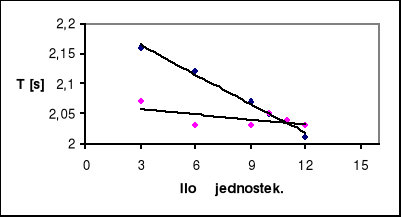
Okresem wahadła rewersyjnego jest wartość T=2,04 [s].
Długość zredukowana (odległość między osiami A i B ) wynosi L=1,03 [m].
Obliczenie przyśpieszenia ziemskiego.
g = ![]()
=![]()
[![]()
]
Wyliczenie błędu metodą różniczki zupełnej.
![]()
![]()
ΔL≅0,001 [m] -szacunkowy błąd wynikający z dokładności przymiaru
liniowego.
ΔT- błąd okresu drgań.
Wyliczenie ΔT jako średniego błędu kwadratowego wartości średniej.
Lp |
1 |
2 |
3 |
4 |
5 |
6 |
T |
2,01 |
2,03 |
2,07 |
2,05 |
2,02 |
2,06 |
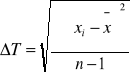
![]()
≈ 0,0006 [s]
Δg = 0,01485 ≅ 0,02 [![]()
]
Ostateczny wynik przy poziomie ufności 68%.
g = (9,77 ± 1,10∗0,02) [![]()
]
![]()
g = (9,77±0,02) [![]()
]
II. Wyznaczanie modułu sprężystości za pomocą wahadła torsyjnego.
Wartość modułu sprężystości:
G = 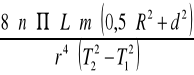
![]()
gdzie: n - ilość obciążników,
d - średnia odległość środka walca obciążającego od osi wibratora,
m - masa walca,
R - promień walca,
L - długość obciążonego pręta,
T1 - okres drgań wibratora nie obciążonego,
T2 - okres drgań wibratora obciążonego,
r - promień pręta.
W naszym doświadczeniu :
n = 2,
d = 0,19 [m]
m = 0,194 [kg]
R = 0,015 [m]
L = 0,94 [m]
T1 = 0,98 [s]
T2 = 1,20 [s]
r = 1,75 *10-2 [m]
Podstawiając do wzoru otrzymujemy :
G = 7,59*106 [Pa]
Szacowanie błędów.
Δd ≈ 0,001 [m]
Δm ≈ 0,001 [kg]
ΔR ≈ 0,001 [m]
ΔL ≈ 0,001 [m]
ΔT1 ≈ 0,01 [s]
ΔT2 ≈ 0,01 [s]
Δr ≈ 0.0001 [m]
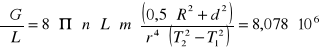
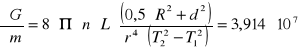
![]()
![]()
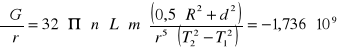
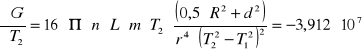
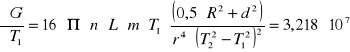
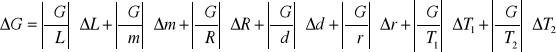
Błąd ΔG wyliczony metodą różniczki zupełnej przy pomocy programu
MathCad 6.0 wynosi: ΔG = ![]()
[Pa]
Wynik naszego doświadczenia: G = ![]()
[Pa]
Wnioski:
Wyniki obliczeń obarczone są pewnym błędem wynikającym z niedokładności obserwatora. Wyznaczenie okresów może być tego najlepszym przykładem.
Metoda wyznaczania przyspieszenia ziemskiego zastosowana w ćwiczeniu jest nieco skomplikowana, dodatkowo utrudnia ją szereg rozbudowanych obliczeń.
Jakość obliczeń poprawia wykorzystany program matematyczny MathCad oraz program do wykonywania wykresów Microsoft Exel.
5
3