Równaniami geometrycznymi

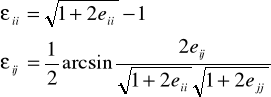
które po rozpisaniu mają postać:

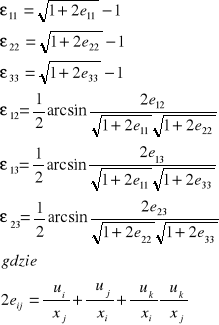
zlinearyzowane związki zwane równaniami Cauchy'ego.

`

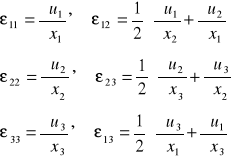
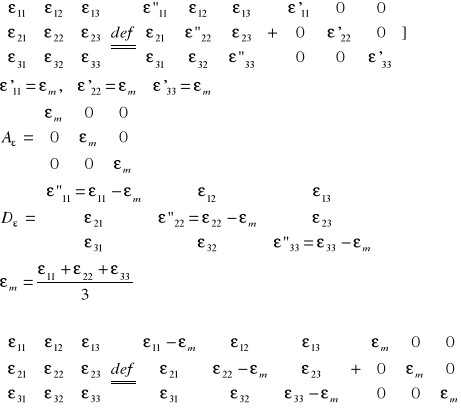
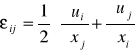
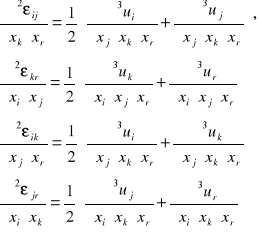
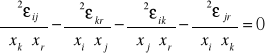
Równań niezależnych jest tylko sześć:

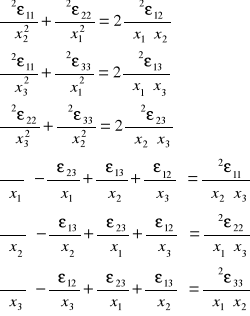
Równanie Hooke'a

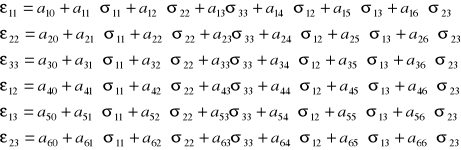
Współczynniki związków są funkcjami trzech zmiennych
. Współczynniki a_i0 zerują się z powodu, że mamy do czynienia z materiałem sprężystym, odkształcenia pojawiają się przy pojawieniu się naprężenia i znikają całkowicie przy zniknięciu naprężeń.

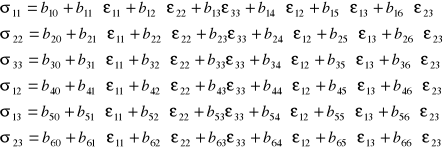
Z powodu zapisanie powyższej macierzy w postaci własnej zeruje odkształcenia ε_ij dla i≠j.

Materiałem izotropowym nazywamy materiał, który w dowolnym punkcie ma jednakowe własności we wszystkich kierunkach. Związki pomiędzy naprężeniami i odkształceniami w danym punkcie są jednakowe

Można również udowodnić ze współczynniki b_ij=b'_ij=0 dla i≥4 a z tego wynika naprężenia σ_ij=0 dla i≠j. To wskazuje na to, że kierunki naprężeń głównych pokrywają się z głównymi kierunkami tensora odkształceń.

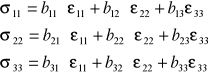
Konsekwencją założenia izotropii jest:

• b₁₁=b₂₂=b₃₃ (wpływ odkształceń liniowych na wartości naprężeń o tym samym kierunku)

• b₁₂=b₁₃=b₂₁=b₂₃=b₃₁=b₃₂=λ ( współczynnik b_ij i≠j określa wpływ j-tego odkształcenia na i-te naprężenie)

redukuje to do dwu liczbę współczynników,

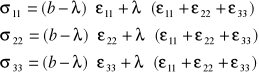
zapisując b-λ=2 G dla powyższego równania odnoszącego się do układu osi głównych, równania zapiszemy

Dla dowolnego układu współrzędnych wzór przyjmie postać:

Powyższy wzór podający zależność pomiędzy naprężeniami a odkształceniami w dowolnym układzie współrzędnych, nosi nazwę równaniami Hooke'a. Współczynniki G i λ noszą nazwę współczynników Lamego i powyższy wzór przyjmuje on postać

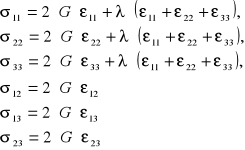
Materiał nazywamy jednorodnym gdy jego własności w każdym punkcie będą jednakowe. W konsekwencji tego G i λ nie będą zależeć od punktu i będą stałymi (stałe materiałowe).

Równanie Hooke'a można również zapisać w innych postaciach. Wyprowadźmy następne z nich:

zrównajmy wskaźniki i,j w powyższym wzorze

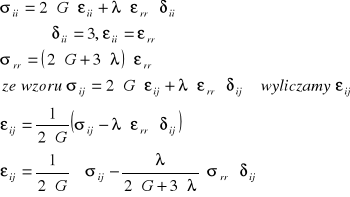
Wyprowadzenie G i ν

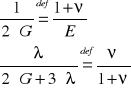
Stałe materiałowe E (moduł Younga) i ν (współczynnik Poissona) i wyraźmy za pomocą nich, stałe Lame'go.

powyższe równanie możemy rozpisać

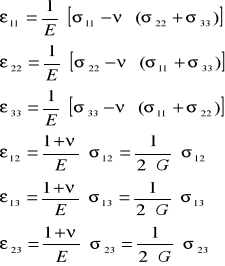
Możemy podać jeszcze jedną zależność pomiędzy naprężeniem a odkształceniem:

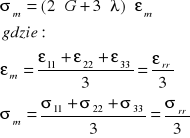
Prawo zmiany postaci i prawo zmiany objętości.

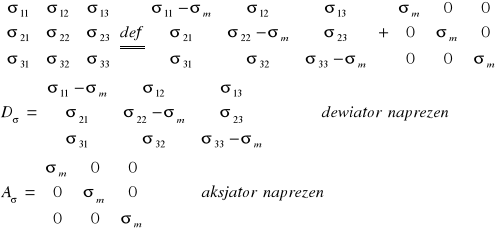
Wzory określające zależności pomiędzy dewiatorami naprężeń i odkształceń oraz aksjatorów naprężeń i odkształceń:

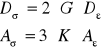
Powyższe wzory są kolejną postacią równań Hooke'a. Pierwsze z nich nosi nazwę prawa zmiany postaci a drugie zaś prawa zmiany objętości.

Jednostkową zmianę objętości obliczamy dodając odkształcenia liniowe.
. Naprężenia określone dewiatorem powodują zmianę postaci, nie powodują natomiast zmiany objętości, relacja między dewiatorami nosi nazwę prawa zmiany postaci.

. Napręzenia określone aksjatorem powoduje zmiane objętości, nie powoduje natomiast zmiany postaci

---