Ruchem drgającym (drganiem lub oscylacją) nazywamy ruch ciała zachodzący wokół stałego położenia. Rozróżniamy ruchy drgające okresowe i nieokresowe. Ruch okresowy, czyli periodyczny jest to taki ruch, którym położenie lub stan ciała powtarza się w jednakowych odstępach czas, zwanych okresem drgań T np. ruch wahadła zegara, ruch tłoka w silniku samochodowym, ruch młota pneumatycznego, ruch struny instrumentu muzycznego.

Położenie punktu materialnego (wychylenie punktu)

gdzie A - amplituda drgań, ω - częstotliwość (częstość) kątowa lub pulsacja; ωt+φ - faza drgań dla t=0 jest równa φ i nazywa się fazą początkową. Drganie to nazywamy drganiem harmonicznym.

Częstotliwość drgań f=1/T=ω/2П. Jednostką częstotliwości jest 1Hz=1 s^-1. Prędkość punktu drgającego otrzymujemy, różniczkując funkcję względem czasu.

Różniczkując ponownie tą zależność względem czasu, znajdujemy przyspieszenie.

Porównując wzory zauważamy że przyśpieszenie jest proporcjonalne do wychylenia.

Drgania swobodne - drgania harmoniczne. Częstotliwość drgań swobodnych ciał nazywamy częstotliwością własną. Drgania swobodne wykonuje ciężarek zawieszony na sprężynie, wahadło matematyczne.

Drgania, jakie wykonuje punkt materialny o masie m pod działaniem siły sprężystości

Zgodnie z II zasadą dynamiki

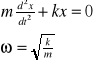
Energia całkowita drgającego harmonicznie punktu materialnego

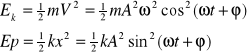
W ruchu harmonicznym energia kinetyczna i potencjalna punktu wykonującego drganie zmieniają się w taki sposób, że ich suma pozostaje stała, co jest zgodne z zasadą zachowania energii mechanicznej, gdyż w przypadku drgań swobodnych straty energii mechanicznej nie występują. Punkt materialny wykonujący drgania harmoniczne nosi nazwę oscylatora harmonicznego nietłumionego.

Drgania tłumione. Jeżeli drgania ciała odbywają się w ośrodku materialnym to wskutek występowania siły oporu ośrodka to siła tłumiąca. Drgania będą zanikać. Niezależnie od natury ośrodka siła tłumiąca F_t jest proporcjonalna do prędkości ciała drgającego jeśli prędkość ta jest niewielka.

Współczynnik proporcjonalności b nazywa się współczynnikiem oporu. Znak minus w powyższym wzorze uwzględnia fakt, że siła F_t jest zawsze skierowana przeciwnie do kierunku ruchu

Uwzględniając działanie siły możemy dla drgań tłumionych, zgodnie z II zasadą dynamiki napisać

czyli

albo

Jest to równanie różniczkowe drgań tłumionych punktu materialnego. Rozwiązaniem tego równania jest funkcja

gdzie
- współczynnik tłumienia,
- pulsacja drgań tłumionych

Skutki działania siły tłumiącej: amplituda drgań maleje z upływem czasu, pulsacja drgań jest mniejsza niż dla drgań swobodnych. Wielkością charakteryzującą drgania tłumione jest tzw. Logarytmiczny dekrement tłumienia. Jest to logarytm naturalny stosunku dwóch amplitud w chwilach t i t+T.

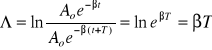
Ruch pełzający charakteryzuje się tym, że ciało wychylone z położenia równowagi nie wykonuje drgań, lecz zbliża się do tego położenia asymptotycznie. Ruch pełzający występuje wtedy, gdy siła oporu ośrodka jest bardzo duża. β=ω - ruch pełzający krytyczny.

Ruch pełzający krytyczny jest wykorzystywany w amortyzatorach pojazdów mechanicznych.

Drgania wymuszone. Jeżeli chcemy, aby opory ośrodka nie tłumiły drgań, to na drgający punkt materialny należy działać odpowiednio zmienną siłą. W przypadku drgań harmonicznych siła ta ma postać

Siłę tę nazywamy siłą wymuszającą. W przypadku drgań wymuszonych mamy

Jest to równanie różniczkowe drgań wymuszonych. Rozwiązaniem tego równania jest

gdzie:

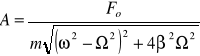
W wyniku działania siły wymuszającej punkt materialny wykonuje drgania harmoniczne z pulsacją, tzn. z taką pulsacją z jaką zmienia się siła wymuszająca. Amplituda drgań wymuszonych jest ściśle określona i zależy od amplitudy siły wymuszającej oraz od jej pulsacji. Początkowa faza drgania zależy od pulsacji.

Faza drgania jest różnicą fazy wychylenia i fazy siły.

Rezonans. Gdy siła wymuszająca działa na drgające ciało z odpowiednią częstotliwością, to amplituda drgań tego ciała może osiągnąć bardzo dużą wielkość nawet przy nie wielkiej sile wymuszającej. Zjawisko to nazywamy rezonansem.

Wartością pulsacji siły wymuszającej, do której amplituda drgań jest maksymalna, nazywa się pulsacją rezonansową. Odpowiadająca jej amplituda nazywa się amplitudą rezonansową.

Amplituda przyjmuje wartość maksymalną, gdy wielomian pod pierwiastkiem osiąga minimum.

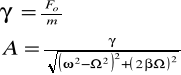
Zjawisko rezonansu jest bardzo rozpowszechnione w przyrodzie i technice. Skutki rezonansu mogą być pozytywne lub negatywne. Rezonans jest wykorzystywany w akustyce przy stosowaniu pudeł rezonansowych oraz głównie w rozmaitych instrumentach muzycznych. Działanie odbiorników radiowych i telewizyjnych jest możliwe dzięki wykorzystaniu rezonansu elektrycznego. W optyce spotykamy się ze zjawiskiem rezonansu, gdy światło o ściśle określonej długości fali ulega pochłonięciu przez atomy; rezonans optyczny leży u podstawy działania laserów. W fizyce jądrowej rezonansem jest związane zjawisko Mössbauera.

Drgania złożone

Składanie drgań harmonicznych równoległych o tej samej częstotliwości. Punkt materialny wykonuje jednocześnie dwa (lub więcej) drgania harmoniczne równoległe o tej samej częstotliwości kołowej, czyli o tej samej pulsacji, lecz różniące się fazą. Drgania nazywamy równoległymi, gdy zachodzą wzdłuż tej samej prostej

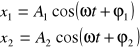
Przy czym występująca między drganiami różnica faz, nosi nazwę przesunięcia fazowego.

Drgania wypadkowe rozważanego punktu jest superpozycją jego drgań składowych, a wychylenie wypadkowe jest sumą jego wychyleń składowych, zatem

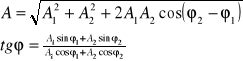
Superpozycja drgań harmonicznych pulsacjach o równoległych jednakowych pulsacjach różniących się fazą, daje w wyniku drganie harmoniczne o tej samej pulsacji. Amplituda drgań składowych dodaje się, gdy ich fazy są zgodne, a odejmują się, gdy fazy te są przeciwne.

Amplitudy drgań składowych dodają się gdy ich fazy są zgodne, a odejmują się gdy fazy te są przeciwne

Składanie drgań harmonicznych równoległych o różnych częstotliwościach.

Superpozycję drgań harmonicznych równoległych o różnych częstotliwościach. W wyniku nałożenia się na siebie takich drgań powstaje okresowe drganie wypadkowe, które na ogół nie jest harmoniczne.

Drgania składowe nazywamy kolejno pierwszym , drugim, itd. drganiem harmonicznym. Pierwsze drganie harmoniczne nazywa się także drganiem podstawowym. Okres drgania wypadkowego jest równe okresowi drgania podstawowego.

Twierdzenie Fouriego - Dowolne drganie okresowe x(t), o okresie T, jest superpozycją drgań harmonicznych i można je wyrazić szeregiem postaci

gdzie

Dudnienie. Przy nałożeniu się drgań harmonicznych niewiele różniących się pulsacjach powstaje drganie złożone, które nazywamy dudnieniem.

Drgania wypadkowe możemy zapisać wzorem

Składanie drgań harmonicznie prostopadłych.

W wielu przykładach spotykamy się z superpozycją dwóch drgań harmonicznych zachodzących wzdłuż prostych prostopadłych względem siebie. Drganie powstałe w wyniku nałożenia się takich drgań jest drganiem złożonym zachodzących w płaszczyźnie. Rozpatrzmy na początku przypadek, gdy pulsacje obu drgań są takie same. Załóżmy że drgania zachodzą wzdłuż osi x i y.

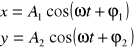
Punkt materialny wykonując oba te drgania jednocześnie, zakreśla na płaszczyźnie pewną krzywą. Równanie tej krzywej można otrzymać po wyeliminowaniu czasu z równań obu drgań.

Złożenia drgań harmonicznych prostopadłych o różnych pulsacjach daje w wyniku skomplikowane krzywe, zwane krzywymi Lissajous.

Obraz złożonych drgań harmonicznych najprościej można otrzymać za pomocą oscyloskopu.

Fale mechaniczne nazywamy fale rozchodzące się w ośrodkach sprężystych. Powstają one w wyniku wychylenia (zaburzenia) jakiegoś fragmentu ośrodka sprężystego z jego normalnego położenia, będącego położeniem równowagi, co w następstwie powoduje powstanie drgania wokół tego położenia. Dzięki sprężystym własnościom ośrodka drgania te są przkazywane kolejno do coraz dalszych jego części i w ten sposób zaburzenia przechodzi przez cały ośrodek. Jest to istota każdego ruchu falowego

Ruch falowy (falą) nazywamy przenoszenie się zaburzenia w ośrodku. Ośrodek jako całość nie przemieszcza się z falą. Różne jego części wykonują jedynie drgania w ograniczonych obszarach przestrzeni. Drgania ośrodka mają pewną energię. Energia jest dostarczana ze źródła. Energia źródła jest przenoszona w ośrodku przez falę. Zjawisko przenoszenia energii bez przenoszenia materii nazywamy transportem energii. Ruch falowy jest związany z transportem energii. Kierunek transportu energii jest zgodny z kierunkiem rozchodzenia się fali, natomiast kierunek drgań cząsteczek ośrodka może być inny. Taka sytuacja istnieje np. w falach rozchodzących się na powierzchni wody.

Rodzaje fal.

Fala poprzeczna -jeżeli kierunek drgań cząsteczek ośrodka jest prostopadły do kierunku rozchodzenia się fali.

Fala podłużna - jeżeli kierunek drgań cząsteczek ośrodka jest równoległy do kierunku rozchodzenia się fali.

Fale poprzeczne i podłużne - fale powierzchniowe na wodzie, w których cząsteczki wody zakreślają tory eliptyczne.

Impuls falowy powstaje wówczas, gdy źródłem fali jest jednorazowe zaburzenie w ośrodku. Fala harmoniczna jest wytwarzana przez źródło wykonujące drgania harmoniczne, w fali harmonicznej wszystkie punkty ośrodka wykonują drgania harmoniczne z różnymi fazami.

Powierzchnia łącząca wszystkie punkty ośrodka, do których dochodzi w danej chwili fala. Zaburzenia w tych punktach są jednakowe. Powierzchnia ta przesuwa się w miarę upływu czasu, a jej ruch obrazuje rozchodzenie się fali. Powierzchnię taką nazywamy czołem fali. Linie prostopadłe do czoła fali i wskazujące kierunek ruchu fali nazywamy promieniami fali. Powierzchnie utworzone przez punkty ośrodka, w których w danej chwili, zaburzenia są jednakowe (mają jednakowe fazy) nazywamy powierzchniami fazowymi. Czoło fali jest jedną z powierzchni falowych. Powierzchnie falowe mogą mieć różne kształty. Ze względu na kształt powierzchni falowych, fale dzielimy na płaskie i kuliste

Fala płaska - jeżeli zaburzenie rozchodzi się w jednym kierunku. Powierzchnie falowe fali płaskiej są płaszczyznami, a promienie fali - liniami prostymi równoległymi do siebie.

Fala kulista - w ośrodku jednorodnym rozchodzi się we wszystkich kierunkach, wychodzących z jednego punktu będącego źródłem fali, powierzchnie falowe fal kulistych są sferami, a promienie fali promieniami sfer. W dużej odległości od źródła fala llista może być traktowana w niewielkim obszarze jak fala płaska.

Prędkość rozchodzenia się fal.

Prędkość rozchodzenia się fali podłużnej w ciele stałym wyraża się wzorem

E - moduł Younga,
- gęstość ciała

Fala poprzeczna rozchodzi się w ciele stałym z prędkością

G - moduł sprężystości postaciowej (moduł sztywności). Na ogół moduł Younga jest większy od modułu sztywności. W danym ciele fala podłużna rozchodzi się szybciej od fali poprzecznej.

Gazy nie mają sprężystości postaci i dlatego nie mogą się w nich rozchodzić fale poprzeczne.

Prędkość fali podłużnej w cieczy wynosi

Gdzie K - moduł ściśliwości cieczy

Prędkość fali podłużnej w gazie wyraża się wzorem

Gdzie p - ciśnienie gazu, a x=c/c

Przykładem fal mechanicznych, rozchodzących się w cele stałym, są fale sejsmiczne.

Fale sejsmiczne - fale te rozchodzą się do miejsca trzęsienia Ziemi lub wybuchu bomby i docierają do innych punktów na Ziemi, rozprzestrzeniając się po cięciwach. Pomiar prędkości podłużnych i poprzecznych fal sejsmicznych umożliwia wyznaczenie modułów sprężystości skorupy ziemskiej. Okazuje się przy tym że fale poprzeczne nie przenikają przez część środkową Ziemi. Dowodzi to słuszności hipotezy, że jądro Ziemi jest w stanie ciekłym

Fala harmoniczna płaska

Zgodnie z podanymi powyżej określeniami, możemy powiedzieć, że rozchodzenie się płaskiej fali harmonicznej polega na przenoszeniu się w pewnym kierunku drgań harmonicznych

W dowolnym punkcie ośrodka wychylnie to wyrazi się równaniem.

Liczba falowa

Jest to równanie fali harmonicznej płaskiej

Długość fali λ nazywamy odległość dwóch punktów fali o fazach różniących się o 2П.

lub

Gdzie f - częstotliwość

Długość fali, zgodnie z definicją, jest równa odległości między dwoma punktami o jednakowym (np. maksymalnym) wychyleniu

Skąd widać, że fala jest okresowa w przestrzeni i w czasie.

Rozchodzenie się fal o rozmaitych kształtach powierzchni falowych, jak również zjawiska ugięcia, odbicia i załamania fal, można opisywać za pomocą Zasada Huygensa - Każdy punkt ośrodka, do którego dociera czoło fali, staje się samodzielnym źródłem wysyłającym fale elementarne.

Dyfrakcja fali (ugięcie) - jeżeli rozchodząca się fala natrafia na jakąkolwiek przeszkodę, to powierzchnia falowa ulega zniekształceniu.

Interferencja fal - zjawisko nakładania się dwóch lub więcej fal o tych samych długościach, więc o tych samych pulsacjach.

Warunkiem koniecznym wystąpienia interferencji fal jest to, aby różnica faz fal nakładających była stała w czasie.

Fala stojąca - fala odbita poruszająca się w kierunku przeciwnym niż fala padająca i superpozycja tych fal daje falę wypadkową. Fale te można opisać równaniami

Stąd fala wypadkowa

Jest to równanie fali stojącej

W przypadku fali stojącej wszystkie cząstki ośrodka (np. struny) wykonują drgania harmoniczne w tej samej fazie. W fali biegnącej amplitudy cząstek drgających są jednakowe, dla fali stojącej natomiast charakterystyczne jest to, że amplitudy drgań cząstek zależą od ich położenia. Punkty o maksymalnej amplitudzie drgań są nazywane strzałkami a punkty, w których amplitudy drgań jest równa zeru czyli punkty nie wykonujące drgań nazywane są węzłami. Fala stojąca jest szczególnym przypadkiem fali, takiej, w której energia drgań nie jest przenoszona, lecz trwale zmagazynowana w poszczególnych punktach ośrodka. Nazywamy go jednak falą stojącą, ponieważ powstaje w wyniku nałożenia się dwóch fal biegnących w przeciwnych kierunkach. Odbicie fali od granicy ośrodka może zachodzić dwojako: ze zmianą fazy i bez zmiany fazy.

Falami dźwiękowymi czyli akustycznymi, nazywamy podłużne fale mechaniczne, mogące rozchodzić się w ciałach stałych, cieczach, gazach. Materialne cząstki ośrodka, w którym rozchodzi się fala dźwiękowa, drgają wzdłuż prostej rozchodzenia się fali. Zakres częstotliwości fal dźwiękowych jest bardzo szeroki. Obejmuje on fale o częstotliwościach od ok. 20 Hz do 20 000 Hz. Fale dźwiękowe powstają w wyniku drgań strun, drgań słupów powietrza oraz drgań różnych płyt i membran. Elementy drgające periodyczne zagęszczają i rozrzedzają otaczające je powietrze. Zagęszczenie następuje w czasie ruchu do przodu, a rozrzedzanie w czasie ruchu powrotnego. Powietrze przenosi te zaburzenia na duże odległości od źródła w postaci fali. Fala taka po dotarciu do ucha jest odbierana jako dźwięk.

Prędkość dźwięku w powietrzu zależy od jego temperatury, ponieważ wraz z temperaturą zmienia się gęstość powietrza. Zależność tą można zapisać wzorem

Gdzie V_o - prędkość dźwięku w temperaturze T_o = 273,16 K

Fale dźwiękowe okresowe dzielimy na tony i dźwięki złożone.

Tony - wywołują zmiany ciśnienia w ośrodku o przebiegu drgań harmonicznych prostych. Dźwięk złożone - powstają w wyniku wzajemnego nakładania się różnych drgań harmonicznych. Dźwięki charakteryzujemy wysokością, barwą i natężeniem. Wysokość dźwięku rośnie ze wzrostem częstotliwości. Barwa dźwięku jest związana z zawartością w fali dźwiękowej wielu drgań o różnych przebiegach i częstotliwościach. Natężenie dźwięku zależy od amplitudy fali dźwiękowej. Dźwiękom o większym natężeniu odpowiada fala dźwiękowa o większej amplitudzie drgań.

Infradźwięki (poddźwięki) - mniej niż 20 Hz, są generowane przez źródła o wielkich rozmiarach.

Ultradźwięki ( naddźwięki)- więcej niż 20 000 Hz, wytwarzane przez specjalne generatory wielkiej częstotliwości.

Ciśnienie

Wychylenie cząsteczek powietrza powodują lokalne zmiany jego ciśnienia

lub

Amplituda ciśnienia fali,
- gęstość ośrodka. Ciśnienie zmienia się w sposób harmoniczny. Ciśnienia fal dźwiękowych nie są duże.

Każda fala przenosi energię drgań źródła fali wyrażona wzorem

gdzie: gęstość - współczynnik sprężystości k=mω² więc

Obliczmy gęstość energii akustycznej tzn. ilość energii w jednostce objętości

Jeżeli na drodze fali ustawimy prostopadle powierzchnię S to w czasie t na powierzchnię tę pada energia fali zawarta w objętości V = SVt

Której moc

Natężenie fali - moc fali przypadającej na jednostkę powierzchni prostopadłej do kierunku rozchodzącej się fali.

Natężenie fali jest więc proporcjonalne do kwadratu amplitudy i kwadratu pulsacji. Natężenie fali inaczej powierzchniowa gęstość mocy.

Poziom natężenia dźwięku (głosu) nazywamy wielkość

Poziom natężenia dźwięku wyraża się w decybelach (dB)

Zjawisko Dopplera - jest to efekt w którym zmienia się częstotliwość fal odbieranych przez obserwatora, w wyniku przemieszczenia się obserwatora lub ośrodka względem ośrodka, w którym rozchodzą się fale.

runku ruchu cząstek ośrodka

---