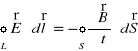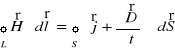Wykład 23

Obwody prądu zmiennego

Obwód prądu zmiennego jest to dowolny zespół połączonych między sobą oporników, kondensatorów i cewek indukcyjnych, w których płyną prądy zmienne w czasie ze stałą częstością
Rozpatrzmy najprostszy przypadek obwodu prądu zmiennego zawierającego opór elektryczny
, kondensator o pojemności
, cewkę o indukcyjności
i źródło prądu zmiennego

. (XXIII.1) Jeżeli rozmiary takiego obwodu nie są zbyt duże, a pojemność kondensatora i indukcyjność nie są nadmiernie małe, to można wykazać, ze natężenie prądu jest prawie stałe w każdej chwili we wszystkich przekrojach obwodu. Takie prądy nazywamy kwaziustalonymi i możemy dla tych prądów

stosować prawa dla obwodów ze stałym prądem. Jeżeli oznaczmy przez
wartość chwilową napięcia na okładkach kondensatora, to zgodnie z drugim prawem Kirchhoffa możemy zapisać

, (XXIII.2)

gdzie

, (XXIII.3)

jest SEM samoindukcji cewki, a
- spadek potencjału na oporze. Biorąc pod uwagę, że

,
,

wzór (XXIII.2) możemy zapisać w postaci

. (XXIII.4)

Oznaczając

,
,
,

przepiszmy równanie (XXIII.4)

. (XXIII.5)

Z równaniem (XXIII.5) już spotkaliśmy na wykładach z pierwszej części Fizyki Ogólnej. To jest równanie wymuszonych drgań oscylatora harmonicznego z tłumieniem. Znajdziemy rozwiązanie równania (XXIII.5), korzystając z innej metody niż to robiliśmy wcześniej.

Rozwiązanie równania (XXIII.5) łatwiej szukać korzystając z liczb zespolonych, a mianowicie będziemy szukali rozwiązanie równania (XXIII.5) w postaci

. (XXIII.6)

Biorąc pod uwagę, że

,
,

i zapisując prawą część równania (XXIII.5) w postaci
, z równania (XXIII.5) otrzymujemy następujące równanie algebraiczne na

. (XXIII.7)

Skąd

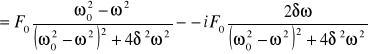
. (XXIII.8)

Ponieważ

,
,
,

rozwiązanie (XXIII.8) możemy zapisać w postaci

, (XXIII.9)

gdzie

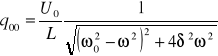
i
. (XXIII.10)

Ostateczne rozwiązanie równania (XXIII.5) przyjmuje postać

. (XXIII.11)

Rzeczywista część rozwiązania (XXIII.12) wynosi

. (XXIII.12)

Rezonans. Dobroć obwodu

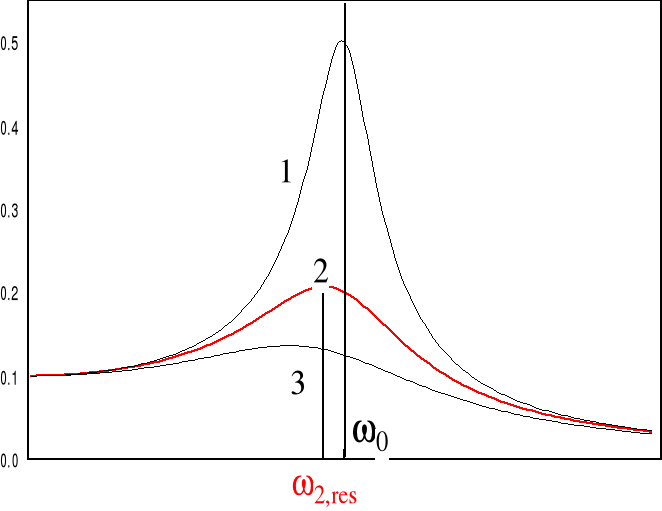
Z zależności
od częstości
wymuszającej SEM, przedstawionej na rysunku, wynika, przy
gwałtownie rośnie wartość
.

Krzywa rezonansowa .

Zjawisko gwałtownego wzrostu amplitudy zmiennego w czasie ładunku elektrycznego, a również wzrost amplitudy prądu zmiennego w obwodzie i amplitudy napięcia na okładkach kondensatora, przy zbliżaniu wielkości pulsacji wymuszającej SEM do wartości nosi nazwę rezonansu elektrycznego. Korzystając ze wzoru (XXIII.12) dla prądu zmiennego, który płynie w obwodzie

otrzymujemy

, (XXIII.13)

gdzie

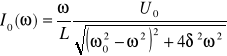
. (XXIII.14)

"Ostrość" rezonansowej krzywej prądu zmiennego (XXIII.14) możemy wyrazić za pomocą szerokości połówkowej względnej, równej
, gdzie
, a częstości
są częstości dla których

. (XXIII.15)

Uwzględniając wzór (XXIII.14), dla częstotliwości
otrzymujemy równanie

.

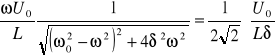
Skąd

. (XXIII.16)

Dwukwadratowe równanie (XXIII.16) ma rozwiązanie

,
.

Skąd dla szerokości połówkowej względnej znajdujemy

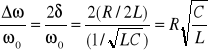
. (XXIII.17)

Wielkość odwrotna do szerokości połówkowej względnej nosi nazwę dobroci
obwodu

. (XXIII.18)

Opory pozorne cewki indukcyjności i kondensatora

Korzystając ze wzoru (XXIII.11) znajdujemy następujący wzór na prąd, który płynie w obwodzie

. (XXIII.19)

Uwzględniając, że
i
, zapiszmy wzór (XXIII.14) w postaci

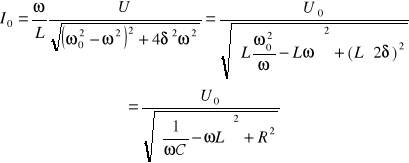
. (XXIII.20)

Po podstawieniu (XXIII.20) do równania (XXII.19) i uwzględnieniu, że
otrzymujemy

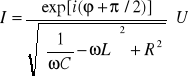
. (XXIII.21)

Oznaczając przez

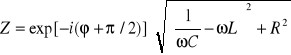
, (XXIII.22)

wzór (XXIII.21) możemy zapisać w postaci

. (XXIII.23)

Wzór (XXIII.23) jest analogiczny do wzoru, wyrażającego prawo Ohma dla prądu stałego (
). W związku z tym urojona wielkość
nazywa się oporem pozornym albo zawadą.

Ponieważ

,
,

,

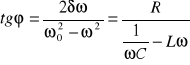
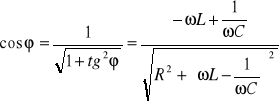
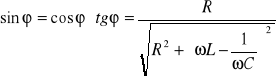
ze wzoru (XXIII.22) znajdujemy

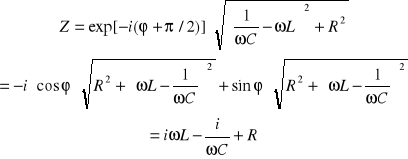
. (XXIII.24)

Ze wzorów (XXIII.23) i (XXIII.24) wynika, że w przypadku obwodów prądów zmiennych możemy stosować prawa Ohma i prawa Kirchhoffa dla obwodów prądu stałego, jeżeli cewce indukcyjności i kondensatorowi przypiszemy opory pozorne

,
. (XXIII.25)

Równania Maxwella

Na poprzednich wykładach zapoznaliśmy z poszczególnymi równaniami pola elektromagnetycznego. Teraz zapiszemy je wszystkie w tradycyjnej formie zwanej równaniami Maxwella.

Pierwsze równanie Maxwella (równanie (XXIII.26a) albo (XXIII.26b)) wyraża prawo indukcji Faradaya: zmienny w czasie strumień magnetyczny jest źródłem wirowego pola elektrycznego.

Całkowa postać równań Maxwella	Różniczkowa postać równań Maxwella
, (XXIII.1a) , (XXIII.2a) , (XXIII.3a) . (XXIII.4a)	, (XXIII.1b) , (XXIII.2b) , (XXIII.3b) . (XXIII.4b)

Z drugiego równania Maxwella (równanie (XXIII.2a) albo (XXIII.2b)) wynika, że pole magnetyczne jest polem wirowym i źródłem tego pola są prądy przewodzenia oraz prądy przesunięcia.

Trzecie równanie Maxwella (równanie (XXIII.3a) albo (XXIII.3b)) jest równoważne prawu Coulomba. Z niego również wynika, że źródłem pola elektrycznego potencjalnego są ładunki elektryczne i linii pola elektrycznego zaczynają się i kończą się na ładunkach elektrycznych.

Czwarte równanie Maxwella (równanie (XXIII.4a) albo (XXIII.4b)) oznacza że w przyrodzie nie istnieją "ładunki" magnetyczne i linii pola magnetycznego są liniami zamkniętymi.

W teorii Maxwella elektryczne i magnetyczne właściwości izotropowego środowiska są określane trzema wielkościami:

1. przenikalnością dielektryczna
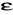
   substancji

, (XXIII.5)

2. przenikalnością magnetyczną
   

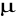
, (XXIII.6)

3. przewodnością elektryczną właściwą
   

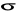
. (XXIII.7)

Układ czterech równań (XXIII.1) - (XXIII.4) oraz trzy równania materialne (XXIII.5) - (XXIII.7) tworzą pełny układ równań teorii pola elektromagnetycznego Maxwella.

Fale elektromagnetyczne. Równanie falowe

Maxwell po raz pierwszy udowodnił, że z równań pola elektromagnetycznego (XXIII.1) - (XXIII.4) wynika możliwość istnienia nawet w pustej przestrzeni (próżni) fal elektromagnetycznych, rozchodzących się z prędkością równej prędkości światła w próżni. Ten fakt pozwolił Maxwellowi założyć, że światło jest niczym innym, jak falą elektromagnetyczną. Rozważmy elektromagnetyczną teorię światła Maxwella i najpierw zapiszmy równania Maxwella w izotropowym ośrodku nie zawierającej ładunków elektrycznych (
) i prądów przewodzenia (
):

, (XXIII.8)

, (XXIII.9)

, (XXIII.10)

. (XXIII.11)

W równaniach (XXIII.10) i (XXIII.11) uwzględniliśmy, że dla izotropowych ośrodków
i
.

Pomnóżmy obustronnie równania (XXIII.8) i (XXIII.9) wektorowe przez

, (XXIII.12)

. (XXIII.13)

Korzystając z tożsamości wektorowej ("bac" minus "cab")

,

znajdujemy dla lewych części równań (XXIII.12) i (XXIII.13)

, (XXIII.14)

. (XXIII.15)

Tu uwzględniliśmy wzór (XXIII.10) (
) i wzór (XXIII.11) (
) oraz wzór

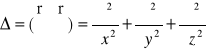
. (XXIII.16)

Dla prawych części równań (XXIII.12) i (XXIII.13), biorąc pod uwagę wzory (XXIII.8) i (XXIII.9), otrzymujemy

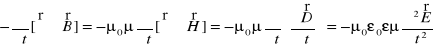
, (XXIII.17)

. (XXIII.18)

Po podstawieniu równań (XXIII.14), (XXIII.15) i (XXIII.17), (XXIII.18) do równań (XXIII.12) i (XXIII.13) ostatecznie otrzymujemy

, (XXIII.19a)

, (XXIII.19b)

gdzie

. (XXIII.20)

Z równaniami typu (XXIII.19a) i (XXIII.19b) już spotykaliśmy w pierwszej części Fizyki Ogólnej. To są tak zwane równania falowe. Określają oni ruch falowy z prędkością
. Przed tym jak rozważać rozwiązania równań falowych rozpatrzmy przypadek próżni (pustej przestrzeni) dla której
. W tym przypadku, jak widać ze wzoru (XXIII.20), prędkość fali jest określona tylko przez fundamentalne stałe
i
i jest równa, jak okazuje się prędkości światła w próżni (
,
)

.

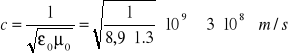
To, że wielkość
pokrywa się z prędkością światła w próżni nie jest przypadkową i wynika z tego, że rozwiązania równań (XXIII.19) reprezentują fali elektromagnetyczne, a światło jest właśnie niczym innym jako falami elektromagnetycznymi. W ośrodku, zgodnie z (XXIII.20), prędkość fali elektromagnetycznej
jest mniejsza od prędkości fali w próżni i wynosi

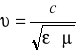
. (XXIII.21)

Udowodnimy teraz, że rozwiązaniami równań (XXIII.19a) i (XXIII.19b) są fale elektromagnetyczny rozchodzące się z prędkością
.

W celu uproszczenia zapisu, zapiszmy równanie (XXIII.19a) tylko dla
- składowej wektora

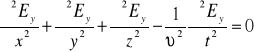
(XXIII.22)

i załóżmy, ze
. Wtedy z równania (XXIII.22) mamy

. (XXIII.23)

Rozwiązanie równania (XXIII.23) łatwo znaleźć wprowadzając nowe zmienne

,
. (XXIII.24)

Rozważając teraz
jako funkcję zmiennych
znajdujemy

, (XXIII.25a)

. (XXIII.25b)

Ze wzorów (XXIII.25) wynika, że

, (XXIII.26a)

. (XXIII.26b)

Korzystając ze wzorów (XXIII.26) otrzymujemy

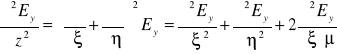
, (XXIII.27)

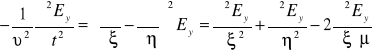
. (XXIII.28)

Po podstawieniu (XXIII.27) i (XXIII.28) do równania (XXIII.23) znajdujemy

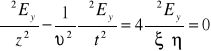
. (XXIII.29)

Łatwo sprawdzić, że rozwiązaniem równania (XXIII.29) jest superpozycja dwóch dowolnych funkcji
i

. (XXIII.30)

Istotnie, różniczkując (XXIII.30) względem zmiennej
otrzymujemy

. (XXIII.31)

Różniczkując następnie (XXIII.31) względem zmiennej
uzyskujemy równanie (XXIII.29).

Przez zmienne
i
(patrz wzór (XXIII.24)) równanie (XXIII.30) możemy zapisać w postaci

. (XXIII.32)

Rozważmy teraz jakiś punkt na krzywej . Wtedy z równości wynika, że wzrostowi czasu odpowiada również wzrost . A zatem punkt będzie przesuwał się w dodatnim kierunku osi z prędkością .

A więc funkcja
reprezentuje falę rozchodzącą się w dodatnim kierunku osi
. Odpowiednie, funkcja
reprezentuje falę rozchodzącą się w ujemnym kierunku osi
.

Udowodniliśmy, że równanie (XXIII.23) jest równaniem fal rozchodzących się z prędkością światła w dodatnim i ujemnym kierunkach osi
.

W zagadnieniach praktycznych najważniejszymi są fale o kształcie

, (XXIII.33)

gdzie
.

W zapisie zespolonym fala (XXIII.33) ma postać

. (XXIII.34)

Powierzchni fazy stałej
) fali określonej wzorem (XXIII.34) - czoło fali, są płaszczyznami prostopadłymi do kierunku rozchodzenia się fali, czyli są prostopadłe do osi
. Fali takie nazywamy falami płaskimi.

Fali postaci (XXIII.33) nazywamy monochromatycznymi (zależą tylko od jednej częstości
) i harmonicznymi (opisuje ich funkcja cos albo sin) falami.

Fali płaskie są dobrym przybliżeniem w przypadku, gdy rozważamy punkty znajdujące się bardzo daleko od źródła fali. Gdyś jednak odległość od źródła nie jest wystarczająco duża, stosujemy przybliżenie fali kulistej. Kulista fala harmoniczna ma postać

, (XXIII.35a)

lub, w zapisie zespolonym:

. (XXIII.35b)

W równaniach (XXIII.35) wielkość
jest odległością punktu od źródła fali.

W przypadku fali kulistej powierzchni stałej fazy
) będą miały postać koncentrycznych powierzchni sferycznych, a nie płaszczyzn.

Oprócz fal płaskich i kulistych stosujemy też czasami przybliżenie fali walcowej. To przybliżenie jest dobrym w przypadku źródła liniowego, albo przy przejściu fali płaskiej przez nieskończenie długą i bardzo wąską szczelinę. Równanie fali walcowej harmonicznej wygląda tak same jak równania (XXIII.35). Jednak teraz w tych równaniach wielkość
, a oś
jest osią symetrii walca, a także źródłem fali.

Rozważmy teraz falę płaską postaci

,
. (XXIII.36)

Z pierwszego równania Maxwella (XXIII.8) znajdujemy

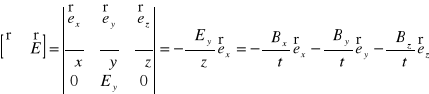
. (XXIII.37)

Skąd

,
. (XXIII.38)

Z dwóch ostatnich równań wynika, że

.

Całkując pierwsze z równań (XXIII.38) względem czasu otrzymujemy

. (XXIII.39)

Tu uwzględniliśmy, że . Biorąc pod uwagę, że oraz wzór (XXIII.39) możemy również zapisać w postaci . (XXIII.40)

Z równań (XXIII.36) i (XXIII.40) wynika, że:

1. drgania pola elektrycznego i magnetycznego są związany między sobą; stąd te fali nazywamy falami elektromagnetycznymi;

2. fale elektromagnetyczne są falami poprzecznymi: wektory
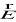
   i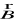
   znajdują się w płaszczyźnie prostopadłej do kierunku rozchodzenia się fali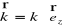
   ;

3. trójka wektorów
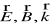
   tworzy trójkę wzajemnie prostopadłych wektorów;

4. wzajemnie prostopadłe wektory
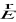
   i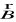
   drgają w jednej fazie, czyli jednocześnie osiągają wartości zerowe i maksymalne.

Wektor Poyntinga - Umowa

Rozważana wyżej fala elektromagnetyczna przenosi w kierunku osi
energię pola elektromagnetycznego. Prędkość przepływu energii w dowolnej fali elektromagnetycznej przez jednostkową powierzchnię opisuje tak zwany wektor Poyntinga - Umowa

. (XXIII.41)

Udowodnimy wzór (XXIII.41) na przykładzie fali elektromagnetycznej (XXIII.36) i (XXIII.39) rozchodzącej się w kierunku osi
.

W ciągu czasu przez powierzchnie prostopadłej do osi przepłynie energia zawarta w objętości , (XXIII.42) gdzie - gęstość objętościowa energii pola elektromagnetycznego

. (XXIII.43)

Z równania (XXIII.40) wynika, że

. (XXIII.44)

A zatem ze wzoru (XXIII.43) znajdujemy

. (XXIII.45)

Po podstawieniu (XXIII.45) do wzoru (XXIII.42) otrzymujemy

. (XXIII.46)

Skąd dla prędkości przepływu energii fali elektromagnetycznej przez jednostkową powierzchnie prostopadła do kierunku propagacji fali uzyskujemy

. (XXIII.47)

103

---