27. Analityczny sposób wyznaczania prędkości obrotowych, przełożenia i zależności między nimi.
Metoda analityczna wyznaczania prędkości obrotowych elementów przekładni
W metodzie analitycznej zaproponowanej przez Willisa rozpatruje się przypadek, w którym obserwator porusza się wraz z jarzmem i określa liczby obrotów kół względem jarzma. Dla takiego obserwatora osie kół są w stałym względem niego i jarzma położeniu, wobec tego przekładnię uważamy za zwykłą o stałych osiach, Oznaczając bezwzględne prędkości obrotowe (mierzone względem stałego układu, np. obudowy) symbolami n1, n2 oraz nh, prędkości obrotowe względem jarzma (obserwatora) określamy jako (n1- nh) oraz (n2 -nh), zatem przełożenie bazowe wynosi:
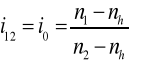
Symbolu i używa się do oznaczania przełożenia w przypadku, gdy jeden wał jest unieruchomiony; wtedy znak i12 oznacza przełożenie pomiędzy wałem 1 i 2 przy zatrzymanym jarzmie h, natomiast znak i1h oznacza przełożenie pomiędzy wałem 1 i jarzmem h przy nieruchomym wale 2. Zawsze indeksy u dołu symbolu i oznaczać będą dwa wały ruchome przekładni obiegowej. Oznaczenie trzeciego wału unieruchomionego jest pomijane.
W przypadku gdy wszystkie trzy wały są ruchome, przełożenie oznacza się literą y z odpowiednimi indeksami u dołu.
Z równania :
![]()
możemy wyznaczyć przełożenia dla różnych kombinacji obrotów, między innymi w następujących szczególnych przypadkach:
1. W przypadku zahamowania jarzma (![]()
) otrzymujemy :
![]()
LUB ![]()
2. Jeżeli n2 = 0, otrzymujemy:
![]()
LUB ![]()
3. Jeżeli n1 = 0, to:
![]()
LUB ![]()
TAK NA MARGINESIE TUTAJ WKLEJAM KILKA ZALEŻNOŚCI
(nie wiem czy potrzebne i ktoś się będzie tego na pamięć uczył ;))) )
28. Obliczanie momentów prostej przekładni obiegowej
Obliczanie momentów
Zgodnie z warunkami równowagi suma momentów działających na trzy wały przekładni musi spełniać równanie
M1+M2+Mh = 0
Z równania tego wynika, że jeden wał obciążony jest momentem o przeciwnym znaku niż dwa pozostałe wały. Wał ten nazywa się wałem sumującym, ponieważ obciążony jest momentem równym bezwzględnej wartości sumy pozostałych dwóch momentów.
W przekładni o bazowym przełożeniu ujemnym (i0 < 0) sumaryczny moment występuje zawsze na wale jarzma, co łatwo zauważyć, jeżeli przyjmie się dwie siły międzyzębne na obwodzie koła obiegowego, których wypadkowa działająca na oś koła obiegowego, a tym samym na jarzmo, wytwarza moment sumaryczny. Oznacza to jednocześnie, że wały kół centralnych są wałami różnicowymi.
W przekładni o bazowym przełożeniu dodatnim (i0 > 0) wał jarzma jest zawsze wałem różnicowym, natomiast wał koła centralnego o mniejszej prędkości, obrotowej, tj. większym momencie obrotowym, jest wałem sumującym. Wynika stąd, że o umiejscowieniu wału sumującego decyduje przełożenie bazowe. W przypadku gdy jest ono większe od 1, większy moment występuje na wale zdawczym, który jest wałem sumującym
Znaki momentów określa się następująco: moment, który działa na wał w kierunku zgodnym z dodatnim kierunkiem prędkości obrotowych, ma znak dodatni, natomiast gdy moment działa w przeciwną stronę, ma on znak ujemny.
Zależności pomiędzy momentami obrotowymi z uwzględnieniem strat tarcia wyznaczamy przy nieruchomym jarzmie, a więc tak jak dla przekładni bazowej. Gdy silnik napędowy połączony jest z wałem 1, wtedy moc oddaną wyrażamy zależnością:
![]()
Gdy natomiast silnik napędza wał 2, wówczas zachodzi zależność:
![]()
gdzie n 12 oraz n21( określają sprawność przekładni przy założonym kierunku przepływu mocy. Powyższe równania możemy sprowadzić do wspólnej postaci
![]()
przy czym wykładnik potęgowy w = ±1.
29. Obliczanie mocy
1. W przypadku nieruchomego jarzma (nh = 0) przekładnia działa jak zwykła przekładnia o stałych osiach kół. Moc doprowadzona do koła 1 jest przenoszona poprzez zazębienie na koło pośredniczące, a stąd na koło wewnętrznie uzębione 2. Ten sposób przenoszenia mocy oznaczany będzie indeksem z (zazębienie).
2. W przypadku nieruchomego koła 2 ruch koła 1 wywołuje przemieszczanie się w tym samym kierunku jarzma h, co oznacza, że maleje względna prędkość koła 1 względem jarzma h. W stosunku do przypadku 1 zmniejsza się więc moc przenoszona przez zazębienie, natomiast pojawia się inny sposób przenoszenia mocy. Odpowiada on przenoszeniu mocy za pomocą sprzęgła zębatego, w którym zęby nie zmieniają swojego wzajemnego położenia. Moc tę określa się mianem mocy sprzężenia lub unoszenia. Zachodzi więc zależność
![]()
gdzie N jest całkowitą mocą przenoszoną przez przekładnię, NZ - przenoszoną przez zazębienie, NS - częścią przenoszoną przez sprzężenie (unoszenie), przy czym
![]()
![]()
Oba rodzaje mocy mają znak dodatni, albowiem kierunek działania momentu pokrywa się z kierunkiem względnej prędkości.
3. Przy założeniu ruchomych wszystkich trzech wałów przekładni może wystąpić szczególny przypadek zrównania się prędkości obrotowych wszystkich wałów. Wtedy zęby nie wykonują wzajemnych ruchów, lecz cała przekładnia zachowuje się jak sprzęgło zębate, przenosząc moc wyłącznie przez sprzężenie, tzn.
![]()
![]()
4. Przy założeniu ruchomych trzech wałów może zaistnieć przypadek, w którym prędkość obrotowa jarzma jest większa od prędkości obrotowej wału 1. Wtedy, zgodnie z poprzednim tokiem rozumowania, moc przenoszenia przez zazębienie będzie ujemna, podczas gdy moc sprzężenia pozostanie nadal dodatnia, tzn.
![]()
![]()
przy czym nadal obowiązuje ogólna zależność:
![]()
30. Warunek poprawnego doboru liczby zębów
W przekładniach obiegowych nawet jednostopniowych muszą być spełnione następujące wymagania:
-liczba zębów w kołach powinna być bliska optymalnej, tj. zapewniającej odpowiedni stosunek współczynników bezpieczeństwa na złamanie i naciski,
-spełniony musi być warunek współosiowości poszczególnych par kół, wiążący w pewien określony sposób liczbę zębów i kąty przyporu,
-koła obiegowe nie mogą dotykać się obwodami, co ogranicza ich maksymalną średnicę, a tym samym i ekstremalną wartość przełożenia,
-montaż musi umożliwiać usytuowanie koła centralnego pomiędzy kołami
obiegowymi o ustalonym już wzajemnym położeniu, warunek ten wyznacza związek
pomiędzy liczbą zębów a liczbą kół obiegowych.
Dodatkowo wskazany jest taki wybór liczby zębów, aby zapewnić optymalne
warunki dynamiczne związane z chwilą wejścia w przypór poszczególnych par
zębów.
Sposób postępowania przy poszukiwaniu związków pomiędzy liczbami zębów
przedstawiony będzie na przykładzie przekładni o ujemnej wartości
przełożenia bazowego.
Warunek współosiowości sprowadza się, po wykorzystaniu znanej zależności:
![]()
do następującej postaci:
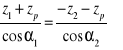
lub jej równoważnej:
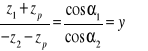
gdzie a - rzeczywista odległość osi, a0 - zerowa odległość osi, z1 - liczba zębów w kole centralnym, z2- liczba zębów w kole wewnętrznie uzębionym (z2< 0), zp - liczba zębów w kole obiegowym, ![]()
-kąt przyporu na średnicy tocznej kół z1 , zp, ![]()
-kąt przyporu na średnicy tocznej kół z2, zp, ![]()
-nominalna wartość kąta przyporu.
W szczególnym przypadku, gdy ![]()
(zęby niekorygowane), powyższe wzory
sprowadzają się do postaci :
![]()
Warunek sąsiedztwa kół obiegowych, przy założeniu minimalnej odległości pomiędzy obwodami kół równej modułowi m, dany jest zależnością:
![]()
gdzie p - liczba kół obiegowych.
Warunkiem montażu kół przy założeniu równomiernego rozmieszczenia kół obiegowych na obwodzie jest spełnienie następującego równania:
![]()
gdzie k jest dowolną liczbą całkowitą.
Oznacza to, że warunek montażu jest zrealizowany, gdy suma bezwzględnych wartości liczb zębów kół centralnych przekładni jest bez reszty podzielna przez liczbę kół obiegowych.
Zazwyczaj przystępując do obliczeń zakłada się wstępnie następujące wartości:
• liczbę kół obiegowych p,
• liczbę zębów w kole centralnym z1
• pożądaną wartość przełożenia bazowego i0; w omawianym przykładzie jest to wart. ujemna.
Ad. 31.
Budowa przekładni falowej.
![]()
Wyszukiwarka
Podobne podstrony:
UPN-opracowanie, Transport Polsl Katowice, 5 semestr, UPN
UPN opracowanie, Transport Polsl Katowice, 5 semestr, UPN
UPN projekt, Transport Polsl Katowice, 6 semestr, Studia 6, MOje, UPN Projekt
MYGA-ZALICZENIE, Transport Polsl Katowice, 6 semestr, Studia 6, Uklady Przeniesienia Napedu, UPN, UP
transport zywnosci, Transport Polsl Katowice, 5 semestr, TPD, Komplet
IM 9, Transport Polsl Katowice, 2 semestr, Inżynieria materiałowa, IM
wytrzymałośc projekt III i, Transport Polsl Katowice, 3 semestr, Rok2 TR
Projekt3 darek staryword, Transport Polsl Katowice, 5 semestr, 5 semestr, PKM3
projekt ze środków nr2, Transport Polsl Katowice, 6 semestr, Studia 6, Materiały Jacek, Środki trans
DD - Opór powietrza, Transport Polsl Katowice, 5 semestr, ŚT, Wyklady, Srodki transportu
moj przenosnik, Transport Polsl Katowice, 6 semestr, Studia 6, Materiały Jacek, Środki transportu, p
Zarządzanie kolokwium wykłady 3, Transport Polsl Katowice, 3 semestr, Rok2 TR
Logistyka sciaga, Transport Polsl Katowice, 3 semestr, Rok2 TR
więcej podobnych podstron