1. Prosty układ napędowy z przekładnią zębatą.

2. Równanie ewolwenty w układzie współrzędnych biegunowych.

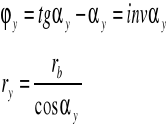
Geometryczne zależności ewolwenty we współrzędnych biegunowych.

3. Zalety i wady zarysu ewolwentowego.

Zalety:

- zęby kół można wykonać przy pomocy noża zębatkowego, który daje się łatwo i dokładnie wykonać,
- może być wykonany metodą obwiedniową, która jest tanią i dokładną metodą wykonania zębów kół,
- przy pomocy tego samego narzędzia można wykonać koła o różnych liczbach zębów, które dają się kojarzyć w dowolne pary, bez względu na liczbę zębów w kole,
- zmiany odległości osi kół nie wpływają na stałość przełożenia,
- kierunek działania siły międzyzębnej nie ulega podczas pracy zmianie,
- przy pomocy tego samego narzędzia można wykonać zęby korygowane.

Wady:
- wysokie naciski pomiędzy zębami, wynikające z tego, że zęby stykają się wypukłościami.

4. Podstawowe parametry geometryczne kołach o zębach prostych.

Podstawowe parametry koła zębatego to: liczba zębów (z), moduł (m), nominalny kąt przyporu (α), średnica koła podziałowego (d), średnica koła wierzchołkowego (da), średnica koła stóp, podstaw (df).

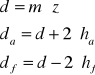
Zarys zębów koła zębatego powstaje w ten sposób, że obwód koła zasadniczego o średnicy „db” dzieli się na „z” równych części i na ich wykreśla się ewolwenty odległe od siebie o stałą wielkość „pb”.
W odległości „s” mierzonej po łuku okręgu podziałowego o średnicy „d” wykreśla się drugą grupę ewolwent odwijanych w przeciwnym kierunku. Obie grupy ewolwent przecinają się w punktach „P”, wyznaczających maksymalną możliwą wysokość zęba.

Pomiędzy podziałką na kole zasadniczym „pb” a podziałką na kole podziałowym ”p” zachodzi zależność wynikająca ze stosunku średnic:

Dla jednoznacznego określenia koła walcowego zębatego o zębach prostych należy podać takie wielkości jak:
z - liczba zębów,
d - średnica podziałowa,
α - nominalny kąt przyporu na średnicy podziałowej,
da - średnica wierzchołkowa,
df - średnica stóp, podstaw,
s - grubość zęba.

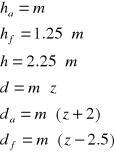
Podstawowymi parametrami koła zębatego są (rys.1 i 2):

z - ilość zębów, m - moduł (wartości znormalizowanych modułów podano w tablicy 1), p - podziałka (mierzona na łuku okręgu podziałowego), pb - podziałka zasadnicza (mierzona na łuku okręgu zasadniczego), d - średnica koła podziałowego, da - średnica koła wierzchołków, df - średnica koła podstaw, db - średnica koła zasadniczego, ha - wysokość głowy zęba, hf - wysokość stopy zęba, h - wysokość zęba, α - nominalny kąt zarysu (α = 20º jest kątem znormalizowanym), s - grubość zęba (teoretyczna), e - szerokość wrębu (teoretyczna), ln - luz międzyzębny normalny, lw - luz wierzchołkowy, a - odległość osi kół współpracujących, x - współczynnik przesunięcia zarysu zęba (współczynnik korekcji), y - współczynnik wysokości zęba, c - współczynnik luzu wierzchołkowego (0,1-0,3)
		Rys. 1. Podstawowe wymiary walcowego koła zębatego.
		Rys. 2. Główne wymiary uzębienia.

5. Luzy w przekładni zębatej.

6. Podcinanie stopy zęba

Podczas nacinania zębów nożem zębatkowym według metody obwiedniowej może nastąpić zjawisko podcinania stopy zęba koła przez zęby narzędzia. Przy dużej liczbie zębów w kole przejście ewolwenty w okolicy okręgu zasadniczego w krzywą ograniczającą stopę zęba następuje w miejscu, gdzie styczne do obu krzywych wzajemnie się pokrywają. Przy małej liczbie zębów w kole część ewolwenty powyżej okręgu zasadniczego zostanie ścięta.

W przypadku gdy nóż zębatkowy nie ma zaokrąglonych naroży oraz gdy nie zastosowano korekcji warunkiem koniecznym i dostatecznym uniknięcia podcinania stopy zęba jest spełnienie zależności:

Podstawiając zależności:

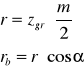
po przekształceniach otrzymujemy wzór na graniczną liczbę zębów, by uniknąć podcinania stopy zęba:

W przypadku korekcji naroża zębatki:

By uniknąć podcinania stopy zęba należy przyjmować liczbę zębów:

7. Czołowa liczba przyporu.

Dla zapewnienia ciągłości pracy kół zębatych, ząb następny musi wejść w zazębienie zanim poprzedni wyjdzie z zazębienia. W przypadku zębów prostych jest konieczne, aby odcinek przyporu „g” był większy od odległości pomiędzy zębami mierzonej wzdłuż tego odcinka a równej podziałce zasadniczej. Wymaga się, aby odcinek przyporu był o 20% większy od podziałki. Stosunek tych odcinków nazywamy wskaźnikiem przyporu czołowego.

8. Korekcja zazębienia (wady, zalety, wpływ na kształt zęba).

W kołach o zazębieniu niekorygowanym linia środkowa narzędzia zębatki toczy się bez poślizgu po kole podziałowym nacinanego koła zębatego.

Wielkość odsunięcia lub dosunięcia narzędzia wyraża się za pomocą współczynnika przesunięcia zarysu x.

Korekcja dodatnia x>0 zarys odsuwany od materiału koła.

Korekcja ujemna x<0 zarys dosuwany do materiału koła.

np. x>0:

• w zazębieniu zewnętrznym → odsuwamy na zewnątrz koła,

• w zazębieniu wewnętrznym → odsuwamy ku wnętrzu koła.

Dodatnie odsunięcie narzędzia w zazębieniu zewnętrznym w kierunku promieniowym o wielkość +xm umożliwia:

• wykonanie koła o małej liczbie zębów bez podcinania stopy zęba,

• uzyskanie dowolnej odległości osi kół przy zachowaniu znormalizowanych modułów i całkowitej liczby zębów,

• poprawienie wytrzymałości zazębienia na złamanie i na naciski (uniknięcie pracy zarysów w pobliżu koła zasadniczego, gdzie ewolwenta ma mały promień krzywizny, a więc naciski są duże).

Wpływ przesunięcia jest tym mniejszy im większa jest liczba zębów.

Korekcja ujemna:

• pogarsza warunki pracy,

• używana jest tylko dla uzyskania potrzebnej odległości osi w kołach o dużej liczbie zębów.

Korekcja dodatnia jest ograniczona zaostrzeniem zęba.

Z praktyki wiadomo, że grubość zęba na kole wierzchołkowym nie może nie może być mniejsza niż 0,4 m, ze względu na luz.

Rodzaje korekcji zazębienia:

• bez przesunięcia (zazębienie niekorygowane)

x₁=x₂=0

• równej sumie przesunięć (korekcja P-0)

x₁=-x₂ albo x₁+x₂=0

• dodatniej lub ujemnej sumie przesunięć
  (korekcja P)

x₁+x₂≠0

Stosując korekcję P-0 zachowuje się taką samą odległość osi i ten sam kąt zarysu, czyli średnica toczna pokrywa się z podziałową. Dodatnie przesunięcie występuje dla zębnika, co pozwala na uniknięcie podcinania, nadając zębom małego koła korzystne kształty z punktu widzenia wytrzymałości zmęczeniowej. Dla dużego koła występuje ujemne przesunięcie zarysu ma mały wpływ na jego kształt.

Dla kół wykonanych z tego samego materiału i z₁=z₂ stosowanie równej sumy przesunięć nie jest celowe.

Dla korekcji P współczynnik x₁ i x₂ dobiera się oddzielnie, aby w optymalny sposób spełnione były warunki wytrzymałościowe kół.

Korekcji P wymaga zmiany odległości osi, natomiast przy korekcji P-0 odległość osi kół nie ulega zmianie.

9. Rozkład sil w zazębieniu kół o zębach skośnych.

10. Obciążenie jednostkowe Q, Q_u.

11. Wpływ przeciążeń zewnętrznych K_p.

W większości przypadków moment obrotowy silnika nie jest stały w czasie, lecz waha się około wartości nominalnej, przyjmując w pewnych chwilach wyższe wartości niż to wynika z nominalnych parametrów silnika napędowego. Wahania te zależą zarówno od rodzaju silnika, jak też maszyny roboczej napędzanej przez przekładnię.

Współczynnik Kp jest liczbą, przez którą należy pomnożyć moment nominalny, aby otrzymać moment obliczeniowy, który działając stale, daje taki sam stopień niezawodności działania przekładni jak rzeczywiście działający, zmienny w czasie moment obrotowy.

W wielu przypadkach zmienia się w czasie nie tylko moment obrotowy, ale także prędkość obrotowa. Ponieważ w obliczeniach zazębienia decydującą rolę odgrywa liczba zmian obciążeń zęba, stąd zachodzi potrzeba wprowadzenia do obliczeń zastępczych wartości uwzględniających zarówno zmienność momentu obrotowego, jak i prędkości.

Istnieją różne metody przeliczania rzeczywistego rozkładu momentu obrotowego na wielkości obliczeniowe. We wszystkich metodach konieczna jest znajomość liczby cykli zmian obciążenia. W tym celu ustala się pewne poziomy momentu obrotowego (klasy) i zlicza całkowitą liczbę zazębień w przeciągu całego planowego okresu pracy przekładni.

12. Wpływ obciążeń wewnętrznych K_d.

Pod względem dynamicznym przekładnia zębata połączona z silnikiem napędowym i maszyną roboczą przedstawia zespół elementów sprężystych i bezwładnych, mający tendencje ulegania drganiom. Przyczyny powstawania drgań, czyli wymuszenia, mogą pochodzić ze źródeł zewnętrznych, np. od silnika lub maszyny roboczej, a także ze źródeł wewnętrznych.

Wpływ źródeł zewnętrznych jest oczywisty, jednak częstotliwość wzbudzania przez źródła zewnętrzne jest bardzo mała w porównaniu z częstotliwością własną kół zębatych, stąd skutki pobudzania są znikome. Natomiast źródła wewnętrzne mają znacznie wyższą częstotliwość pobudzania i dlatego mają większe znaczenie w dynamice przekładni.

Przekładnia zębata o przeznaczeniu czysto kinematycznym (a więc przekładnia nie przenosząca mocy) charakteryzuje się praktycznie brakiem odkształceń sprężystych i dlatego może być rozpatrywana wyłącznie z punktu widzenia geometrii i kinematyki. Wymagania stawiane takiej przekładni są znane z rozdziału poświęconego geometrii zazębienia. Zarys musi być tak dobrany, aby zapewniał stałość przełożenia. Ewentualną przyczyną przyspieszeń i drgań są błędy kinematyczne.

Przekładnia przeznaczona do przenoszenia momentu obrotowego pracuje w nieco odmiennych warunkach niż przekładnia kinematyczna. Pod działaniem sił elementy przekładni ulegają odkształceniom, między innymi także zęby ulegają ugięciom i spłaszczeniom. Okazuje się, że same tylko odkształcenia są poważną przyczyną drgań, na wet jeżeli nie występują jednocześnie błędy kinematyczne.

13. Model dynamiczny przekładni zębatej (Mullera).

14. Nierównomierne obciążenie na szerokości koła K_r, K_rt, K_s.

Obciążenie nie rozkłada się równomiernie na całej szerokości koła, dlatego zachodzi potrzeba uwzględnienia w obliczeniach nierównomierności rozkładu. Wpływ błędów wykonania, np. wichrowatości osi, uwzględnia się za pomocą współczynnik Kr, wpływ odkształceń sprężystych wywołujących najczęściej również nierównomierny rozkład obciążenia na szerokości koła uwzględnia się za pomocą współczynnika Kro, natomiast wpływ sztywności zęba zmiennej wzdłuż linii styku zębów, a występującej w kołach o zębach śrubowych, za pomocą dodatkowego współczynnika Ks.

Nierównomierny rozkład obciążenia na szerokości koła jest wywołany trzema przyczynami:

1) Wadliwa obróbka mechaniczna prowadzi między innymi do powstania następujących odchyłek mających bezpośredni wpływ na ślad przylegania: nierównoległość osi, wichrowatość osi i błąd kierunku linii zęba. Na skutek tych błędów zęby nie stykają się ze sobą na całej szerokości koła, lecz najczęściej z jednej tylko strony. Skutki odchyłek wykonawczych zostały ujęte za pomocą współczynnika Kr.

2) Często się zdarza, że koła wykazujące prawidłowy ślad przylegania zębów podczas technicznego odbioru bez obciążenia, wykazują w okresie normalnej pracy (a więc pod pełnym obciążeniem) ślad nieprawidłowy, również najczęściej jednostronny. Wynika to z wpływu odkształceń głównie wałów i korpusów kół powstałych pod działaniem przenoszonego obciążenia. Te wpływy ujęto za pomocą współczynnika Kr0.

3) W kołach o zębach prostych ząb wchodzi w zazębienie jednocześnie na całej szerokości koła. Mimo, że jego sztywność zmienia się wzdłuż drogi zazębienia, to zmiany te powstające jednocześnie na całej szerokości koła nie wywołują nierównomiernego rozkładu obciążenia.

Inaczej sprawa przedstawia się w przypadku zębów śrubowych. Tam poszczególne przekroje koła i zęba znajdują się w innej fazie zazębienia, a więc wykazują inną sztywność, stąd też inny udział w przenoszeniu obciążenia, a tym samym nierównomierny jego rozkład na szerokości koła. Wpływ skośnego położenia zębów na nierównomierność rozkładu uwzględniono za pomocą współczynnika Ks, którego wartość w przypadku zębów prostych wynosi 1.

Bez względu na przyczynę nierównomierności rozkładu, odpowiedni współczynnik Kr, Kr0 lub Ks może być zdefiniowany jako stosunek maksymalnego lokalnego obciążenia zęba przypadającego na jednostkę długości do wartości średniej wyliczonej przy założeniu równomiernego rozkładu. Biorąc pod uwagę proporcjonalność odkształceń i obciążeń, można powyższe twierdzenie zapisać w postaci

gdzie: pmax - maksymalna wartość obciążenia przypadającego na jednostkę szerokości koła, pm - średnia wartość obciążenia przypadającego na jednostkę szerokości koła, fmax - maksymalne lokalne odkształcenie zęba, fm - średnie odkształcenie zęba na szerokości koła.

15. Wyznaczanie naprężeń u podstawy zęba.

16. Wytrzymałość zmęczeniowa zębów.

17. Obliczanie współczynnika bezpieczeństwa na złamanie.

18. Obliczanie współczynnika bezpieczeństwa na naciski.

19. Zależności między współczynnikami bezpieczeństwa.

20. Rozkład przełożenia na stopnie.

21. Dobór liczb zębów.

22. Dobór względnej szerokości zębnika.

23. Dobór współczynnika korekcji kół.

24. Zalety i wady przekładni obiegowych.

25. Budowa prostej przekładni obiegowej.

26. Def. Przełożenia bazowego, sprawności bazowej.

27. Analityczny sposób wyznaczenia prędkości obrotowej, przełożenia i zależności między nimi.

28. Obliczanie momentów prostej przekładni obiegowej.

29. Obliczanie mocy.

30. Warunki poprawnego doboru liczby zębów.

31. Budowa przekładni falowej.
    

---