Materiały do wykładu

Wykład 4

Stopa dochodu w okresie do wykupu - YTM (yield to maturity)

Jeżeli cena obligacji jest ustalona (np. przez rynek) to możemy obliczyć stopę zwrotu, przy której ta cena została ustalona, czyli rozwiązać równanie:

P = Fr·a_n,p + C·v_pⁿ

Ze względu na stopę procentową p:

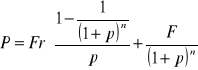
Tak wyznaczoną stopę procentową (stopę zwrotu) często oznaczamy YTM.

Zauważ analogię do IRR.

Przykład 1

Dana jest obligacja z dwuletnim terminem do wykupu, o wartości nominalnej F = 100, cenie P = 98,88 oprocentowana r = 4,2% rocznie.

Odsetki są płacone co roku.

Oblicz stopę dochodu w okresie do wykupu (YTM).

Rozwiązanie

Należy rozwiązać równanie kwadratowe ze względu na p:

P = Fr / (1+p) + (Fr+F) / (1+p)²

P·(1+p)² - Fr·(1+p) - (Fr+F) = 0

Niech x = 1+p.

98,88·x² - 4,2·x - 104,2 = 0

Zachodzi:

 = (-4,2)² - 4·98,88·(-104,2) = 41.230,82

^0,5 = 203,0537

Rozwiązujemy równanie kwadratowe, uwzględniając pierwiastki mające sens ekonomiczny:

x = (-b ± ^0,5) / 2a

(1+p) = (4,2 + 203,0537) / (2·98,88)

1+p = 1,048006

p = 4,80%

Odpowiedź:

Stopa dochodu w okresie do wykupu YTM = 4,80%.

Przykład 2

Dana jest trzyletnia obligacja zerokuponowa o wartości nominalnej F = 100, cenie P = 87,63.

Oblicz stopę dochodu w okresie do wykupu (YTM).

Rozwiązanie

Należy rozwiązać równanie ze względu na r:

P·(1+r)ⁿ = F

r = (F / P)^1/n -1

r = (100 / 87,63)^1/3 - 1

r = 1,14116^1/3 - 1

r = 0,00450

r = 4,50%

Odpowiedź:

Stopa dochodu w okresie do wykupu YTM = 4,50%.

Jaką przyjąć strategię kupna obligacji

Jeśli wartość obligacji jest większa niż cena obligacji - należy je kupić.

Jeśli wartość obligacji jest mniejsza niż cena obligacji - należy je sprzedać.

Jeśli stopa dochodu w okresie do wykupu jest większa od wymaganej przez nas - należy je kupić.

Jeśli stopa dochodu w okresie do wykupu jest mniejsza od wymaganej przez nas - należy je sprzedać.

Przykład 3

Mamy obligacje Skarbu Państwa, dla których YTM = 6,35%. Wymagana przez nas stopa zwrotu (rynkowa stopa zwrotu dla tego typu inwestycji) r = 6,38% Czy powinniśmy sprzedać posiadane obligacje, czy też dokupić?

Odpowiedź

Stopa dochodu w okresie do wykupu jest mniejsza od wymaganej przez nas - należy je sprzedać.

Przykład 4

Mamy obligacje Skarbu Państwa, dla których YTM = 6,24%. Wymagana przez nas stopa zwrotu (rynkowa stopa zwrotu dla tego typu inwestycji) r = 6,21% Czy powinniśmy sprzedać posiadane obligacje, czy też dokupić?

Odpowiedź

Stopa dochodu w okresie do wykupu jest większa od wymaganej przez nas - należy je kupić.

Przykład 5

Aktualna cena pewnych obligacji wynosi 101,12 zł.

Według naszych obliczeń wartość tych obligacji wynosi 101,09 zł.

Powinniśmy dokupić obligacje, czy sprzedać posiadane.

Odpowiedź

Wartość obligacji jest mniejsza niż cena obligacji - należy je sprzedać.

Przykład 6

Aktualna cena pewnych obligacji wynosi 100,98 zł.

Według naszych obliczeń wartość tych obligacji wynosi 101,01 zł.

Powinniśmy dokupić obligacje, czy sprzedać posiadane.

Odpowiedź

Wartość obligacji jest większa niż cena obligacji - należy je kupić.

Pytanie

Jak wyznaczana jest wymagana stopa zwrotu?

Odpowiedź

Na rynku są ci którzy oferują kapitał do pożyczki (kredytodawcy) i ci którzy chcą kapitał pożyczyć (kredytobiorcy).

Ustala się cena (stopa procentowa) pożyczki za inwestycję - pożyczkę bez ryzyka.

Ta cena to realna stopa procentowa r_r .

Jeśli na rynku występuje inflacja w wysokości r_i , to nominalna stopa procentowa r określona jest wzorem:

1 + r = (1 + r_r)( 1 + r_i)

Tak więc nominalna stopa procentowa r wynosi:

r = r_r+ r_i + r_r·r_i

Przy niskiej inflacji, często opuszczamy składnik r_r·r_i

r = r_r+ r_i

Dodatkowo wymagana jest premia za płynność r_pp i premia za ryzyko r_pr .

Tak więc końcowa wymagana stop zwrot to:

r = r_r+ r_i + r_pp + r_pr

Przykład 4

Oblicz wymaganą stopę zwrotu, czynnik oprocentowującym czynnik dyskontujacy jeśli:

inwestycja pozbawiona ryzyka daję 3,1%,

spodziewana inflacja to 1,25%,

premia za płynność to 0,22%

premia za ryzyko 5,55%.

Odpowiedź

R = 3,1% + 1,25% + 0,22% + 5,55% = 10,12%

Czas trwania obligacji - duration (Macaulay - 1938)

Czas trwania D obligacji określamy wzorem:

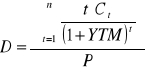
Gdzie:

D - czas trwania;

P - wartość (cena);

YTM - stopa dochodu w okresie do wykupu;

C_t - płatność w chwili t.

Przykład 5

Oblicz czas trwania czteroletnich obligacji o wartości nominalnej 100, oprocentowanych 4,20% z odsetkami płatnymi rocznie.

Stopa dochodu w okresie do wykupu obligacji wynosi YTM = 3,50%.

Rozwiązanie

P = 4,2 / 1,035 + 4,2 / 1,035² + 4,2 / 1,035³ + 104,2 / 1,035⁴

P = 4,0580 + 3,9207 + 3,7882 + 90,8043

P = 102,5712

P = 102,57

D = [ 1·4,2 / 1,035 + 2·4,2 / 1,035² + 3·4,2 / 1,035³ + 4·104,2 / 1,035⁴ ] / 102,5712

D = 3,7679

Czas trwania (duration) tych obligacji D = 3,77.

Czas trwania obligacji zerokuponowych

D = n·F·vⁿ / P

D = n·F·vⁿ / F·vⁿ

D = n

Obligacje zerukuponowe mają czas trwania równe terminowi zapadalności.

Przykład 6

Oblicz czas trwania trzyletnich obligacji zerokuponowych o wartości nominalnej 100zł i cenie rynkowej (wartości) 97,20zł.

Odpowiedź (bez liczenia). D = 4.

Czas trwania portfela obligacji.

Mamy portfel obligacji P składający się z n rodzajów obligacji o czasach trwania równych D₁, D₂, …, D_n odpowiednio.

Udział i-tego rodzaju obligacji w portfelu wynosi w_i .

Czas trwania portfela D_P jest średnią ważoną czasów trwania obligacji i wynosi:

D_P = w₁·D₁ + w₂·D₂ + … + w_i·D_i + … + w_n·D_n

Przykład 7

Mamy portfel złożony z trzech rodzajów obligacji.

Obligacje o czasie trwania 0,8 stanowią 20% portfela.

Dwuletnie zerokuponowe obligacje stanowią połowę wartości portfela.

Resztę stanowią obligacje o czasie trwania 2,56 roku.

Oblicz czas trwania portfela.

Rozwiązanie

D_P = 0,2 · 0,8 + 0,5 · 2 + 0,3 · 2,56 = 1,928

Inwestujemy w obligacje z myślą osiągnięcia ustalonej wartości ze sprzedaży portfela w ustalonym momencie czasu w przyszłości.

Strategia uodporniania portfela.

Chcemy skonstruować portfel o ustalonym czasie trwania.

Przykład 8

Chcemy osiągnąć wartość portfela K = 100.000 za dwa lata.

Dostępne są jedynie obligacje:

1. Czteroletnie F = 100, r = 10%, odsetki rocznie, sprzedawane po wartości nominalnej,

2. Roczne zerokuponowe sprzedawane po 90,91 o wartości nominalnej F = 100.

Uwaga, jak łatwo zauważyć YTM = 10% dla obu obligacji.

Dla obligacji czteroletnich wynika to z faktu, że sprzedawane są po wartości nominalnej.

Dla obligacji rocznych liczymy wprost.

Obliczanie wartości i czasu trwania dla YTM = 10% dla obligacji czteroletnich.

t	0	1	2	3	4
Kt		10	10	10	110	suma
Kt·v^t		9,090909	8,264463	7,513148	75,13148	100
t·Kt·v^t		9,090909	16,52893	22,53944	300,5259	348,6852
					D =	3,486852

Czas trwania dla obligacji rocznych zerokuponowych wynosi D = 1.

Obliczanie składu portfela.

Niech w oznacza wagę obligacji czteroletnich w portfelu.

Waga obligacji rocznych wynosi (1-w).

Żądamy by portfel miał czas trwania 2. Musi więc zachodzić równość:

2 = 3,486852 · w + 1 · (1-w)

Skąd

1 = 2,486852 · w

w = 0,40221

Czyli obligacji czteroletnich ma być 40,22% , zaś jednorocznych 59,78% .

Wartość obecna inwestycji (przy założeniu stopy zwrotu i = 10%) wynosi:

PV = 100.000 / 1,1² = 82.644,63

Z tego powinniśmy przeznaczyć 40,22% na zakup obligacji czteroletnich czyli:

82.644,63zł · 0,4022 = 33.239,67zł .

Czyli

33.239,67zł / 100 zł = 332,3967 obligacji.

Na zakup obligacji rocznych powinniśmy przeznaczyć:

82.644,63zł · 0,5978 = 49.404,96 zł.

Czyli powinniśmy kupić:

49.404,96 zł / 90,91 zł = 543,4491 obligacji.

Możemy jednak kupić tylko całe obligacje, a więc kupujemy:

333 sztuki obligacji 4 letnich i

544 sztuki obligacji jednorocznych.

Rachunek efektywności projektów inwestycyjnych

Projekt inwestycyjny

Dla naszych celów przez projekt inwestycyjny będziemy rozumieli ograniczony w czasie strumień przepływów pieniężnych. To ograniczenie czasowe będziemy nazywali czasem trwania (czasem życia) projektu.

Przykład 9

Sześcioletni projekt inwestycyjny z konwencjonalnymi przepływami finansowymi:

Czas	Wydatki	Wpływy	Przepływy
0	1200		-1200
1	350	100	-250
2	80	400	320
3	80	700	620
4		700	700
5		700	700
6		700	700

Metody oceny projektów inwestycyjnych możemy podzielić na dwie klasy:

metody proste ;

metody dyskontowane.

Przyczyny oceny projektu inwestycyjnego:

Ocena pojedynczego projektu - pomoc w podjęciu decyzji o rozpoczęciu inwestycji lub jej zaniechaniu.

W tym przypadku mówimy o rachunku bezwzględnej efektywności projektu inwestycyjnego.

Porównanie kilku rozważanych projektów inwestycyjnych, wybór najlepszego.

Metody proste

Prosty okres zwrotu

Przy konwencjonalnych przepływach pieniężnych pierwszy moment, gdy skumulowane przepływy pieniężne są dodatnie, a więc jest to moment gdy zwrócone zostaną zainwestowane kapitały.

Prosty wskaźnik rentowności

PI - profitabilty index

Iloraz sumy dodatnich przepływów pieniężnych przez moduł sumy ujemnych przepływów pieniężnych.

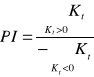
Możemy realizować jedynie te projekty dla których PI > 1.

Jeżeli PI < 1, to wydatki są większe niż wpływy.

Takiego projektu nie realizujemy.

Metody dyskontowane

Dyskontowany okres zwrotu

Zakładamy konwencjonalne przepływy kapitałowe.

Dyskontowany okres zwrotu to pierwszy moment, gdy zdyskontowane skumulowane przepływy pieniężne są większe od zera.

Jest to moment gdy zwrócone zostaną zainwestowane kapitały liczone poprzez (PV) wartości zaktualizowane.

Dyskontowany wskaźnik rentowności

PI - profitabilty index

Iloraz sumy dodatnich zdyskontowanych przepływów pieniężnych przez moduł sumy ujemnych zdyskontowanych przepływów pieniężnych.

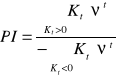
Możemy realizować jedynie te projekty dla których PI > 1.

Jeżeli PI < 1, to zdyskontowane wydatki są większe niż zdyskontowane wpływy.

Takiego projektu nie realizujemy.

Wartość bieżąca netto - NPV (net prezent value)

Suma zdyskontowanych przepływów pieniężnych.

Jeden z najważniejszych współczynników opisujących inwestycję.

Mając do wyboru kilka inwestycji wybieramy tę, która ma największą wartość NPV.

Wewnętrzna stopa zwrotu - IRR (internal rate of return)

Stopa procentowa przy której NPV = 0.

IRR jest bardzo ważnym współczynnikiem pozwalającym ocenić ryzykowność inwestycji.

Przykład 10

Oceń inwestycję opisaną w przykładzie 9.

Metody proste.

Czas	Przepływy	Przepływy skumulowane
0	-1200	-1200
1	-250	-1450
2	320	-1130
3	620	-510
4	700	190
5	700	890
6	700	1590

Prosty okres zwrotu to 4 lata.

Po raz pierwszy na koniec czwartego roku pojawiły się dodatnie skumulowane przepływy kapitałowe.

PI - prosty indeks zyskowności

PI = (3200 + 620 + 700 + 700 + 700) / (1200 + 250)

PI = 3040 / 1450 = 2,096552

Przy ocenie metodami prostymi inwestycja wygląda atrakcyjnie.

W czwartym roku jest już zwrot zainwestowanych kapitałów.

Każda zainwestowana złotówka przynosi ponad dwa złote dochodu.

Metody dyskontowe

Koszt kapitału r = 18,74%.

Czas	Przepływy	Przepływy zdyskontowane	Przepływy zdyskontowane skumulowane
0	-1200	-1200,00	-1200,00
1	-250	-210,54	-1410,54
2	320	226,96	-1183,58
3	620	370,34	-813,24
4	700	352,14	-461,10
5	700	296,56	-164,51
6	700	249,76	85,22

Dyskontowany okres zwrotu to 6 lat.

PI dyskontowany indeks zyskowności

PI = (226,96 + 370,34 + 352,14 + 296,56 + 249,76) / (1200 + 210,54)

PI = 1495,76 / 1410,54 = 1,060417

W dyskontowanej analizie przedsięwzięcie wygląda gorzej.

Zwrot zainwestowanych pieniędzy dopiero pod koniec szóstego okresu.

Każda zainwestowana złotówka daje 1,06 zł.

NPV - wartość bieżąca netto

NPV = 85,22

Wewnętrzna stopa zwrotu wynosi IRR = 20,58%.

MatFinUb W4.doc Matematyka finansowa i ubezpieczeniowa

P. Zaremba 8/8

---