PODSTAWY METODY HARMONICZNEJ PŁYWÓW

Podstawy teorii pływów świadczą o niemożliwości wykorzystania w praktyce uzyskanych tam równań do przewidywania wartości pływów i ich przebiegu w czasie, w warunkach realnego oceanu, a szczególnie w jego strefach brzegowych. Niemniej droga wskazana przez Laplace'a doprowadziła do opracowania analizy harmonicznej pływów, co okazało się jak do tej pory jedynym efektywnym sposobem rozwiązania tego zadania. Metoda analizy harmonicznej opracowana przez W. Thomsona była udoskonalona przez wielu badaczy: G. Darwina, A. Doodsona, H. Warburga, A. Defanta i innych. Można ją uznać za podstawową wykorzystywaną aktualnie metodę przewidywania pływów.

Siły pływotwórcze, niezależnie od bardzo złożonego ruchu ciał, które je wywołują, charakteryzują się okresowością, co oznacza, że można wybrać taki okres czasu, w przeciągu którego dokonują one pełnego cyklu zmian. Dzięki te­mu w wahaniach poziomu morza przejawia się analogiczna okresowość, nieza­leżnie od znacznych zakłóceń będących wynikiem oddziaływania dna i wybrzeży.

Główna idea analizy harmonicznej oparta jest na tym, że jeżeli zjawisko pływu w swoim zasadniczym charakterze jest zjawiskiem okresowym, to poten­cjał siły pływotwórczej można rozłożyć na proste składowe harmoniczne, a bar­dzo skomplikowane krzywe rzeczywistych wahań poziomu morza na szereg fal, z których każda ma charakter prostych harmonicznych wahań.

W 1921 roku A. Doodson rozłożył potencjał sil pływotwórczych na 385 składowych długookresowych. Pełna analiza harmoniczna wymaga wieloletniego okresu obserwacji i nawet teoretycznie nie jest w pełni rozwiązana. Dla celów praktycznych uwzględnia się tylko główne składowe i często wystarcza 8-11 elementarnych fal pływu.

ISTOTA ANALIZY HARMONICZNEJ W NAWIGACJI

Uproszczonym sposobem obliczania krzywej pływu według składowych harmonicznych jest sposób zwany metodą admiralicji. Jej rozwinięciem jest analiza harmoniczna. W tym celu zapoznajmy się z istotą tej metody.

Każdą falę pływu możemy traktować jako sumę szeregu prostych fal harmonicznych:

gdzie:

f - współczynnik,

H - średnia wartość amplitudy rzeczywistej danej składowej,

(E + u) - faza fali,

g⁰ - opóźnienie w fazie.

Pozostaje pytanie, jak znaleźć składowe, które dodane do siebie dadzą wypadkową falę pływu. Aby na nie odpowiedzieć należy rozpatrzeć pływ teoretyczny zwany zrównoważonym. Zgodnie z teorią wysoka woda ma wystąpić w momencie maksymalnej siły pływotwórczej, a w szczególności wysoka woda pływu syzygijnego ma wystąpić w momencie nowiu lub pełni Księżyca. Obserwacje pływu rzeczywistego naturalnie nie potwierdzają tych przypuszczeń i przykładowo dla wybrzeży niemieckich na Morzu Północnym opóźnienie syzygijne dochodzi do 3 dób. Obserwując więc pływ rzeczywisty zauważymy, że wysokość i momenty wód wysokich i niskich tego pływu różnią się w każdej miejscowości od wysokości i momentów pływu zrównoważonego, a dodatkowo w każdej miejscowości jest inna wysokość średniego poziomu morza nad poziomem zera mapy. Wynika z tego, że nie sposób byłoby prognozować wartości pływu (momentów wód wysokich i niskich oraz ich wysokości), opierając się tylko na teorii pływu zrównoważonego, a więc bez uprzedniej obserwacji i analizy rzeczywistej krzywej pływu w danej miejscowości.

Na podstawie przebiegu krzywej pływu wykreślonej pływomierzem w danej miejscowości (przy czym w grę wchodzi odpowiednio długi horyzont czasu obserwacji) i po rozłożeniu tej krzywej na składowe harmoniczne otrzymano składowe o takim samym okresie, jak odpowiadające im składowe pływu zrów­noważonego. Stwierdzono również różnice w amplitudach oraz to, że składowe harmoniczne pływu rzeczywistego są opóźnione w fazie w stosunku do składo­wych pływu zrównoważonego. W części III ATT dla wyszczególnionych tam portów mamy podane stałe harmoniczne (Harmonie Constants) głównych skła­dowych harmonicznych pływu rzeczywistego, a mianowicie:

• opóźnienie w fazie (g⁰),

• średnią wartość amplitudy rzeczywistej danej składowej (H),

• średni poziom morza (MSL).

Te stałe zostały określone na podstawie analizy harmonicznej wykreślonej krzywej pływu w danym porcie.

Opóźnienie w fazie (g⁰) wyraża opóźnienie momentu wody wysokiej składowej harmonicznej pływu rzeczywistego w danej miejscowości, w odniesieniu do momentu wody wysokiej pływu zrównoważonego i zawiera poprawkę na różnicę czasu między czasem strefowym w danej miejscowości a czasem Greenwich.

Amplituda (H), średnia wartość amplitudy składowej harmonicznej pływu rzeczywistego w danej miejscowości.

Średni poziom morza (MSL) wysokość średniego poziomu morza nad zerem mapy.

Znając te stałe harmoniczne pływu rzeczywistego oraz składowe harmoniczne pływu zrównoważonego, możemy znaleźć składowe harmoniczne pływu rzeczywistego, a następnie wykreślić krzywą pływu. W wydawanych corocznie ATT na każdy dzień w roku w tabeli VII podano kąty pływu (Tidal Angles) i współczynniki, zwane również współczynnikami amplitud (Factors), czterech głównych składowych harmonicznych pływu zrównoważonego: M₂, S₂, K₁, i O₁.

Dobowe kąty pływu to fazy wody wysokiej poszczególnych składowych li­czone od południka zerowego Greenwich, czyli czas jaki upłynie od południka zerowego do momentu wystąpienia wody wysokiej danej składowej, pomnożony przez jej prędkość kątową. Jeżeli podzielimy dobowy kąt pływu przez prędkość kątową odpowiedniej składowej, to uzyskamy czas wystąpienia pierwszej wody wysokiej w danym dniu dla tej składowej. Oprócz dobowych kątów pływu, w tablicy VII podano współczynniki amplitud (Factors), które uwzględniają zmiany wielkości średnich sił pływotwórczych, a więc zmiany wysokości amplitud składowych harmonicznych. Jeżeli przykładowo, zmiana deklinacji Księżyca spowoduje przyrost amplitudy składowej harmonicznej pływu zrównoważonego o 0,1, to we wszystkich miejscach na kuli ziemskiej amplitudy odpowiadających im składowych rzeczywistych również wzrosną o 0,1.

Wartości kątów pływu (Tidal Angles) dla składowych półdobowych i dobowych (M₂, S₂, K₁ i Q₁) podane w tabeli VII obliczono najpierw w następujący sposób:

gdzie:

E - argument astronomiczny (tabela VIII),

u - poprawka korygująca (Nodal Correction).

Następnie uwzględniono wpływ dodatkowych składowych, których prędkości kątowe odpowiadają w przybliżeniu prędkościom głównych składowych harmonicznych i dla których można również przyjąć podobne opóźnienia fazowe, jak w przypadku głównych składowych. I tak głównym składowym półdobowym M₂ przyporządkowane są składowe N₂, V₂, L₂, 2N₂ μ₂, υ₂, a składowej S₂ - K₂, T₂, R₂, natomiast głównym składowym dobowym K₁ przyporządkowane są: P₁, L₁, M₁, Π₁, φ₁, Θ1, Ψ1, SO₁, a składowej O_l - Q₁, P₁, 2Q₁, δ₁.

Wartości poszczególnych składowych harmonicznych pływu rzeczywistego będą więc scharakteryzowane następująco:

1. Faza wody wysokiej liczona od południka strefowego w danej miejscowości równa się opóźnieniu w fazie (g⁰) + faza wody wysokiej pływu zrównoważonego (TA).

2. Amplituda równa się średniej rzeczywistej wartości amplitudy (H) razy współczynnik amplitudy (f).

3. Wartość średniego poziomu (A₀) równa jest średniej wysokości średniego poziomu (ML) + poprawka sezonowa zmian średniego poziomu.

4. Prędkość kątowa danej składowej.

W omawianej metodzie admiralicji przyjęto prędkości składowych półdobowych 29 °/h, a składowych dobowych 14,5 °/h. Najpierw więc znajdujemy wypadkową M₂ + S₂, a następnie K₁ + O₁ i dla tych wypadkowych obliczamy wysokość pływu co l godzinę. Następnie wystarczy zsumować rzędne i otrzy­mamy krzywą pływu.

Dla przykładu obliczymy i następnie wykreślimy krzywą dla następujących danych składowych harmonicznych pływu rzeczywistego:

M₂ = 048° H = 0,80 m

S₂ = 187° H = 0,14 m

K₁ = 013° H = 0,12 m

O₁ = 088° H = 0,17 m

Wysokość średniego poziomu morza 1,20 m.

Obliczamy wypadkową fazy wody wysokiej oraz amplitudę składowych harmonicznych M₂+ S₂. Wypadkową fazę i amplitudę składowych harmonicz­nych o jednakowej prędkości kątowej (przyjmiemy 29 °/h) uzyskamy sumując wektory składowe.

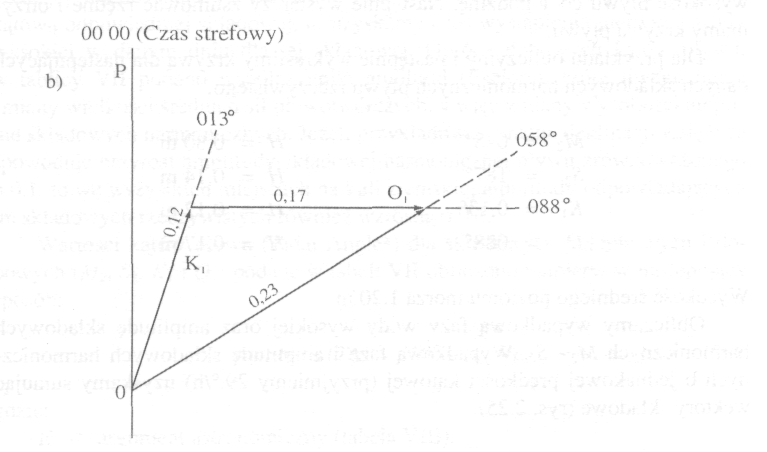
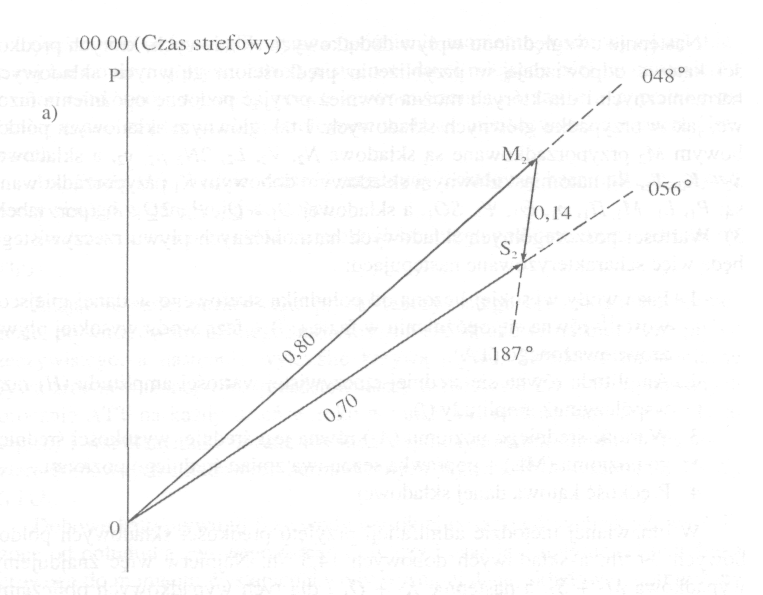
Rys. 1 Obliczanie fazy i amplitudy wody wysokiej składowych M₂ + S₂ (a)

oraz K₁ + O₁ (b)

Amplituda wypadkowa równa się 0,70; a fazy wody wysokiej równają się 056°, co odpowiada godzinie 0156, gdyż:

Teraz przystępujemy do wyznaczania punktów krzywej pływu składowych M₂ + S₂, które obliczamy zgodnie z zależnością:

gdzie:

- wysokość pływu dla obranego momentu t w odniesieniu do

średniego poziomu (m),

H - amplituda wypadkowa (m),

Α - prędkość kątowa składowych (°/h),

t - przedział czasu od momentu wystąpienia wody wysokiej do

dowolnego momentu (h),

(α · t) - odstęp kątowy od momentu wody wysokiej do przyjętego

momentu, czyli faza pływu (°).

Ponieważ zmiana wysokości pływu jest kosinusoidalna, a prędkość kątowa wynosi 29°/h, wysokości dla obranych momentów równają się amplitudzie 0,70 pomnożonej przez cosinus oddalenia kątowego tych punktów od momentu wy­stąpienia wody wysokiej o godzinie 0156.

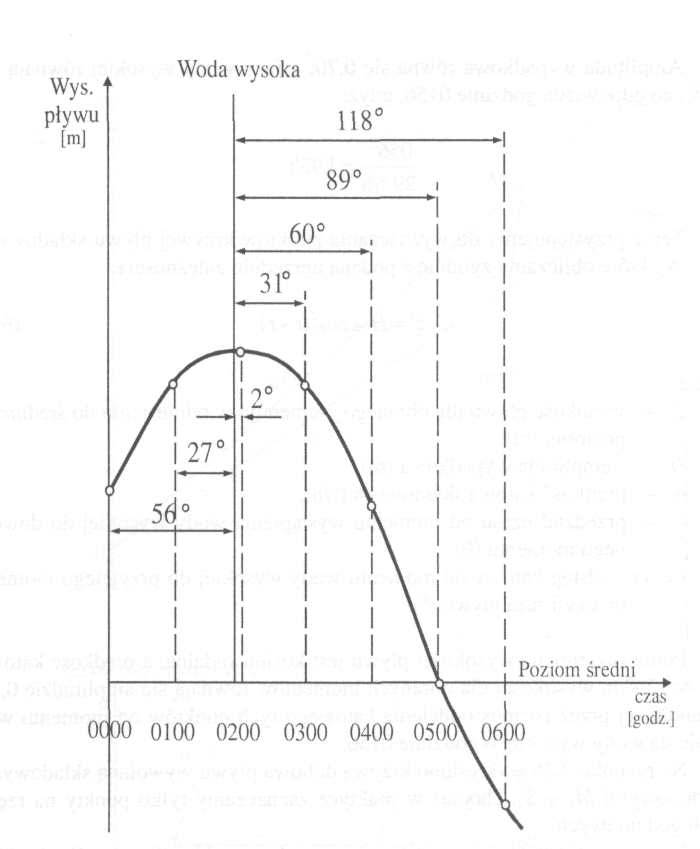
Na poniższym rysunku wykreślono krzywą dobową pływu wywołaną składowymi półdobowymi M₂ + S₂, chociaż w praktyce zaznaczamy tylko punkty na rzędnych godzinowych.

Rys. 2 Wysokość pływu wywołana składowymi półdobowymi M₂ + S₂

Godz.

0000 wysokość pływu nad średni poziom = 0,70 · cos56° = 0,39

0100 wysokość pływu nad średni poziom = 0,70 · cos27° = 0,62

0156 wysokość pływu nad średni poziom = 0,70 · cos0° = 0,70

0200 wysokość pływu nad średni poziom = 0,70 · cos2° = 0,70

0300 wysokość pływu nad średni poziom = 0,70 · cos31° = 0,60

0400 wysokość pływu nad średni poziom = 0,70 · cos60° = 0,35

0500 wysokość pływu nad średni poziom = 0,70 · cos89° = 0,01

0600 wysokość pływu nad średni poziom = 0,70 · cos118° = - 0,33

………………………………………………………………………..

2400 wysokość pływu nad średni poziom = 0,70 · cos280° = 0,12 86

Następnie obliczamy wypadkową fazę wody wysokiej oraz amplitudę składowych K₁ + O₁, podobnie jak w przypadku składowych półdobowych, zakładamy jednak ich prędkość kątową 14,5 °/h (rys. 1).

Wypadkowa amplituda składowych K₁ + O₁ wynosi 0,23 m, a faza wody wysokiej 058°, co odpowiada godzinie 0400
. Następnie, przystępujemy do obliczania wysokości pływu dobowego K₁ + O₁ (rys. 3).

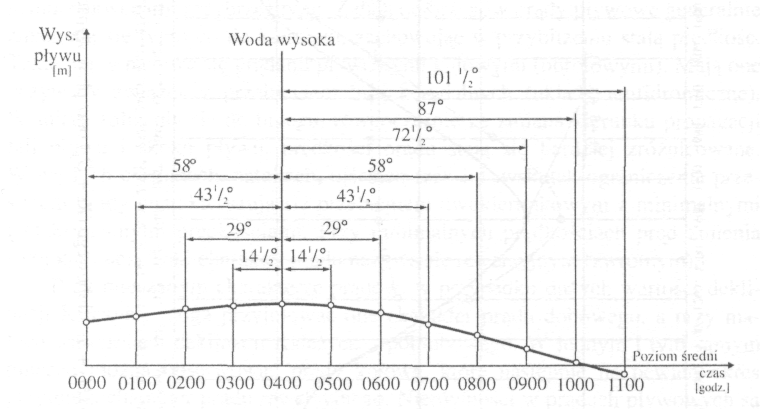
Rys. 3 Wysokość pływu wywołana składowymi dobowymi K₁ + O₁

Godz.

0000 wysokość pływu nad średni poziom - 0,23 · cos58° = 0,12

0100 wysokość pływu nad średni poziom = 0,23 · cos43,5° = 0,17

0200 wysokość pływu nad średni poziom = 0,23 · cos29° = 0,20

0300 wysokość pływu nad średni poziom = 0,23 · cos14,5° = 0,22

0400 wysokość pływu nad średni poziom = 0,23 · cos0° = 0,23

0500 wysokość pływu nad średni poziom = 0,23 · cos14,5° = 0,22

0600 wysokość pływu nad średni poziom = 0,23 · cos29° = 0,20

0700 wysokość pływu nad średni poziom = 0,23 · cos43,5° = 0,17

0800 wysokość pływu nad średni poziom = 0,23 · cos58° = 0,12

0900 wysokość pływu nad średni poziom = 0,23 · cos72,5° = 0,07

1000 wysokość pływu nad średni poziom = 0,23 · cos87° = 0,01

1100 wysokość pływu nad średni poziom = 0,23 · cosl0l,5° = - 0,04

……………………………………………………………………………

2400 wysokość pływu nad średni poziom = 0,23 · cos290° = 0,08

Rysunek 4 przedstawia nam wykreśloną krzywą pływu jako sumę pływu wywołanego składowymi półdobowymi M₂ + S₂ oraz dobowymi K₁ + O₁. W praktyce nie wykreślamy krzywej M₂ + S₂ ani K₁ + O1, tylko zaznaczamy wy­sokość pływu na rzędnych godzinowych najpierw składowych półdobowych, a następnie od tak zaznaczonych punktów odmierzamy wysokości pływu dobo­wego, czyli sumujemy bezpośrednio rzędne pływu półdobowego i dobowego.

Dalszym rozwinięciem w wykreślaniu krzywej pływu metodą admiralicji jest sposób z wykorzystaniem wydawnictwa Admiralty Method of Tidal Prediction NP 159.

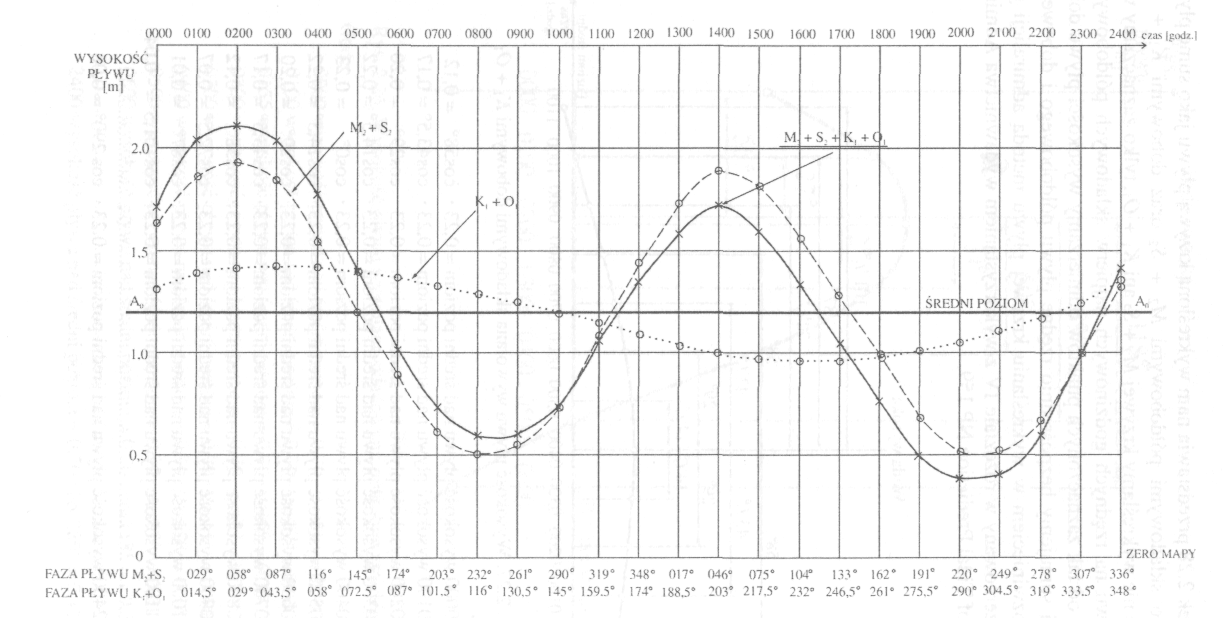
Rys. 4 Krzywa składowej pływu półdobowego (M₂ + S₂), dobowego (K₁ + O₁) oraz pływ wypadkowy (M₂ + S₂ + K1 + O₁)

1

---