Wykład 3

Estymacja modelu liniowego KMNK

Szacujemy parametry w/w równania (Klasyczna Metoda Najmniejszych Kwadratów):

URN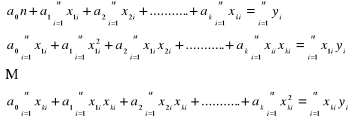

,

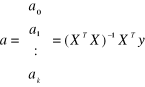
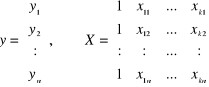
Parametry rozkładu składnika losowego (parametry struktury stochastycznej modelu)

• Wariancja reszt
  , (k+1) - liczba szacowanych parametrów

• Odchylenie standardowe reszt
  

• Współczynnik zmienności losowej
  

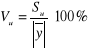
• Współczynnik zbieżności
  

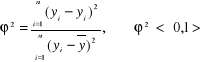
• Średnie błędy ocen
  - macierz wariancji i kowariancji: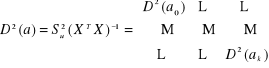
  ,

• Współczynnik determinacji
  

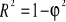
• Współczynnik korelacji wielorakiej
  

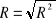
Weryfikacja modelu:

- merytoryczna - polega na ocenie czy uzyskane wyniki, a zwłaszcza oceny parametrów strukturalnych są zgodne z istniejącą teorią, doświadczeniem i oczekiwaniami (rząd wielkości parametrów, ich znaki)

- formalna, m.in.:

1. weryfikacja statystycznej istotności ocen parametrów strukturalnych - ma na celu sprawdzenie czy parametry zostały oszacowane dostatecznie dokładnie, a tym samym czy zmienne, przy których stoją te parametry istotnie wpływają na zmienną endogeniczną. Przeprowadzamy weryfikację przy pomocy testu t Studenta, dla każdego parametru:

(rozkład t Studenta z n-(k+1) st. swobody)

to nie ma podstaw do odrzucenia
, czyli parametr statystycznie nieistotny, tym samym zmienna, przy której stoi nieistotnie wpływa na zmienną endogeniczną (Y)

to odrzucenia
na korzyść
,czyli parametr statystycznie istotny

2. ocena dobroci dopasowania modelu do obserwacji empirycznych:

3. badanie wybranych własności reszt - reszty powinny mieć charakter losowy, symetryczny; nie powinny wykazywać autokorelacji (nie powinny być skorelowane) - warunek ten dotyczy tylko modeli szacowanych na podstawie szeregów czasowych; powinna być zachowana jednorodność wariancji.

Badanie losowości reszt - można je przeprowadzić za pomocą testu serii:

reszty:
oznaczamy a,
oznaczamy b,
pomijamy,

otrzymujemy, w ten sposób ciąg złożony z elementów a i b, w którym możemy zaobserwować serie - podciągi złożone z elementów jednego rodzaju; odczytujemy liczbę serii =
i porównujemy ją z wartością krytyczną
odczytaną z tablic rozkładu serii dla przyjętego poziomu istotności
oraz
i
stopni swobody (
- liczba elementów a,
- liczba elementów b);
to nie ma podstaw do odrzucenia hipotezy o losowości reszt,
to hipotezę o losowości reszt odrzucamy.

ZADANIE

1. Na podstawie danych:

yi (przychód w tyś. zł.)	4	6	8	12	14
xi (liczba zatrudnionych / dziesiątki osób)	1	1	2	5	3

1. wyznaczyć i zweryfikować jego istotność przyjmując
   ,

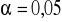
2. oszacować liniowe równanie regresji Y względem X oraz oszacować i zinterpretować parametry struktury stochastycznej modelu,

3. przedstawić dane i model graficznie,

4. przeprowadzić skróconą weryfikację modelu.

2. Na podstawie danych:

	10	40	20	70	40
	1	2	0	3	4
	1	1	1	1	-4

a) oszacować liniowe równanie regresji: ,

b) oszacować i zinterpretować parametry struktury stochastycznej modelu,

c) przeprowadzić skróconą weryfikację modelu.

3. W pewnym przedsiębiorstwie zbadano zależność pomiędzy indywidualną wydajnością pracy sześciu pracowników Y (szt. wyrobu na miesiąc), a stażem pracy
(w miesiącach), faktem posiadania przez pracownika gospodarstwa rolnego
(0-nie; 1-tak) oraz liczbą dzieci
. Zebrano następujące dane:

21 24 32 41 40 52	1 2 3 5 4 5	1 1 1 1 1 0	1 1 2 0 2 0

Należy:

1. stosując metodę Hellwiga wybrać optymalną kombinację zmiennych objaśniających,

2. oszacować parametry strukturalne i struktury stochastycznej modelu liniowego z wybranymi zmiennymi,

3. zinterpretować wyniki,

4. przeprowadzić skróconą weryfikację modelu.

4. Budując model ekonometryczny zmiennej endogenicznej Y zaproponowano wstępnie trzy potencjalne zmienne objaśniające:
,
,
. W oparciu o dane:

10 38 45 90 127	-20 -10 -10 10 30	2 1 0 -1 -2	6 7 8 9 10

Należy:

1. stosując metodę Hellwiga wybrać optymalną kombinację zmiennych objaśniających,

2. oszacować parametry strukturalne i struktury stochastycznej modelu liniowego z wybranymi zmiennymi,

3. zinterpretować wyniki,

4. przeprowadzić skróconą weryfikację modelu.

---