POLITECHNIKA WARSZAWSKA

WYDZIAŁ INŻYNIERII LĄDOWEJ

INSTYTUT KONSTRUKCJI BUDOWLANYCH

ZESPÓŁ KONSTRUKCJI DREWNIANYCH

GRZEGORZ PIÓRCZYŃSKI

Politechnika Warszawska

Wydział Inżynierii Lądowej

Semestr IV; Grupa 4

R. A. 2006/2007

ZADANIE 2 - Zaprojektować belkę stropową o przekroju złożonym dla następujących danych:

Dane:

● Obciążenie: stałe g_0k=0.5 kN/m² ; zmienne p_0k=2.0 kN/m²

● Rozstaw belek: a = 0.8 m

● Rozpiętość belki w świetle podpór: l = 3.0 m

● Klasa drewna: C24

● Współczynnik k_mod: 0.90

● Rodzaj przekroju: belka skrzynkowa drewniana

● Łączniki: gwoździe

Klasa drewna C24
E_0,mean=11000 MPa = 1100 kN/cm²
f_m,k = 24 MPa
f_t,0,k= 14 MPa
f_v,k = 2,5 MPa

F_c,90,k= 5,7 MPa

1. Obciążenia i siły przekrojowe

Obciążenie charakterystyczne przypadające na belkę:

Stałe: g_k= g_0k ·a = 0.5·0,8 = 0.4kN/m,
Zmienne p_k = p_0k·a = 2.0 · 0,8 = 1.6kN/m

Obciążenie obliczeniowe:

Stałe: g_d = g_k·1.15 = 0.4·1,15= 0.46kN/m,
Zmienne p_d = p_k·1.4 = 1,6·1,4 = 2.24 kN/m

Obciążenie całkowite;

• charakterystyczne
  q_k= 0.4+1,6 = 2.0 kN/m

• obliczeniowe:

q_d = 0.46+2.24 = 2.7 kN/m

Rozpiętość obliczeniowa:

l₀ = 1,051 = 1,05·3.0m= 3.15 m.
Moment obliczeniowy
M₀ = 0,125·q_d·l₀² = 0.125 ·2.7·3.15² = 3.35 kNm
Siła poprzeczna

V₀ = 0,5·q_d·l₀ = 0.5·2.7·3.15= 4.25 kN.

2. Dobór przekroju:

Wysokość całkowita H ~ 1/15- 1/20 l.
H ~ 0.2 - 0.15 l.
Przyjęto 150 mm

Grubość środnika: b_w/2 ≥ 2a_4c;

Zakres dopuszczalnych średnic gwoździ:

1/6t ≥ d ≥ 1/11t,
długość wbicia gwoździa w środnik I₁ > 8d (7.4.2.1.(4))

W przypadku półek o grubości 25 mm:
25/6≥ d ≥25/11; 4.2 mm >d > 2.3 mm
Przyjęto gwoździe 3.0/60.
Minimalna grubość środnika b_w/2 = 10d = 10x3.0 = 30 mm. (Tablica 7.4.2.1)

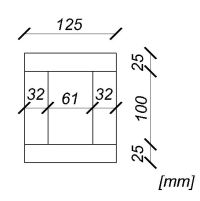
Przyjęto półki 2x25x125 mm i środniki 2x32x100 mm.

Długość zakotwienia gwoździa:
l₁ = 60 - 25 - 1 - 1,5·3.0 = 29.5 mm > 8d = 24 mm.

2. Wyznaczenie nośności gwoździ

f_h,1,k=0.082ρ_kd^-0.3=0.082·380·3.0^-0.3 = 22.4MPa = 2.24 kN/cm²

M_y,k= 180d^2,6 = 180·5.0^2,6 = 11819,38 Nmm = 0.313 kNcm
M_y,d = M_y,k/γ_z = 0.313/1.1 = 0.284 kNcm

grubość elementów składowych złącza lub długość zakotwienia łącznika

wytrzymałość obliczeniowa na docisk w elemencie o grubości

średnica trzpienia łącznika

25 mm

29.5 mm

d = 3.0 mm

R_da = 1.164 kN

R_db = 1.373 kN

R_dc = 0.528 kN

R_dd = 0.605 kN

R_de = 0.544 kN

R_df = 0.566 kN
R_dmin = 0.528 kN

Moduł podatności gwoździ
K_ser = ρ_k^1,5d^0,8/25 = 380^1.5·3.0^0.8/25 = 713.56 N/mm= 7.14kN/cm (tabl. 7.2)

K_u = 2/3K_ser = 2/3·7.14 = 4.76 kN/cm (wz.7.2.a)

3. Wyznaczenie efektywnego momentu bezwładności

A₁ = 2.5·12.5 = 31.25 cm²

Moment bezwładności brutto:

2A₁a₁² =2·31.25·6.25² = 2441.41 cm⁴
I_br = 565.88 + 2441.41 = 3007.29 cm⁴

Moment statyczny półki:
S₁ = A₁·a₁ = 31.25·6.25= 195.31 cm3

a_1,min= 10d = 3.0 cm
a_1,max = 40d = 12 cm

s_1,min = a_1,min/2 = 1.5 cm
s_1,max = a_1,max/2 = 6 cm (tabl. 7.4.2.1),

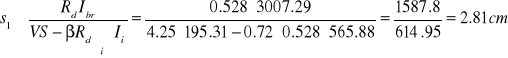
Przyjęto: s_i = 2.5 cm, rozstaw łączników; a_i = 2s_i = 5 cm.

Współczynnik redukcyjny:
, gdzie

Zastępczy moment bezwładności:



4. SGU - sprawdzanie ugięcia
u_fin=u_inst(1+k_def)
h=2·2.5+10=15cm
L=315 cm
L/h=21>20 zatem: nie uwzględniamy wpływ sił poprzecznych:
u_inst=u_M[1+η₁(h/l)²]

Ugięcie wyznaczamy sumując ugięcia cząstkowe od obciążeń składowych o różnych

czasach trwania - dla danej klasy użytkowania.

W I klasie użytkowania konstrukcji

k_def.g = 0,60 - obciążenie stałe

k_def.p - 0,25 - obciążenie użytkowe (średniotrwałe)

Ugięcie chwilowe od obciążenia stałego: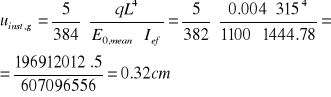


u_inst,g= u_inst,p
u_fin=u_inst.g(1+k_def,g)+ u_inst.p(1+k_def,p)=0.32·1.6+0.32·1.25=0.512+0.4=0.91cm

u_fin<u_dop=315/250=1.26cm

5. Stan graniczny nośności
5.1. Łączniki:

5.2 Naprężenie normalne

Wytrzymałość obliczeniowa na zginanie

α=M/I_ef=335/1444.78=0.23kN/cm³

δ_w=Mz_red/2·I_ef=M·h₂/2·I_ef= α·h₂/2=1.15kN/cm²<f_m,d

Naprężenia w osi pasa rozciąganego:

Naprężenia krawędziowe: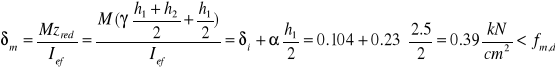



5.3 maksymalne naprężenie styczne
Wytrzymałość obliczeniowa na ścinanie

6. Oparcie belki na podporze

Ze względów konstrukcyjnych przyjęto 10 cm
Rzeczywista długość belki:
L=l+2·l_op=300+2·10=320 cm

7. Rozmieszczenie łączników

a_3t=15d=15·3=45 mm

Przyjęto n_rz=62

Ostatecznie:
a₁=50 mm

a_3t=75 mm
a_4c= 16 mm

---