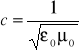Podaj i krótko omów równania Maxwella Omów widmo promieniowania fal elektromagnetycznych Omów zjawisko interferencji fal elektromagnetycznych na dwóch szczelinach Zdefiniuj światło liniowo spolaryzowane podaj sposoby otrzymywania światła spolaryzowanego W jaki sposób można poznać strukturę kryształu Omów zjawisko polaryzacji światła przez odbicie Omów zjawisko fotoelektryczne Narysuj zależność energii wybitych przez światło elektronów od częstości światła Podaj omów prawo Plancka opisujące promieniowanie ciała doskonale czarnego. Podaj związek między energią kwantów światła i długością fali światła Opisz koncepcję de Broglie'a fal materii Elektrony to cząstki czy fale; uzasadnij Metody otrzymywania i zastosowanie promieniowania X ? Przedstaw zasadę nieoznaczoności Heisenberga Napisz i skomentuj równanie Schroedingera Podaj równanie Schroedingera dla cząstki w nieskończonej studni potencjału i przedstaw na rysunku możliwe energie cząstki. Podaj rodzaje wiązań występujących miedzy atomami i omów jedno z nich. Omów strukturę pasmową ciała stałego. Omów zależność oporności elektrycznej metali i półprzewodników od temperatury. Wyjaśnij działanie diody i tranzystora.

	Prawo	Równanie	Czego dotyczy	Doświadczenie
1	Gaussa dla elektryczności		ładunek i pole elektryczne	Przyciąganie, odpychanie ładunków (1/r^2). Ładunki gromadzą się na powierzchni metalu
2	Gaussa dla magnetyzmu		pole magnetyczne	nie stwierdzono istnienia monopola magnetycznego
3	indukcji Faradaya		efekt elektryczny zmieniającego się pola magnetycznego	indukowanie SEM w obwodzie przez przesuwany magnes
4	Ampera (rozszerzone przez Maxwella)		efekt magnetyczny zmieniającego się pola elektrycznego	prąd w przewodniku wytwarza wokół pole magnetyczne prędkość światła można wyliczyć z pomiarów EM

2. wszystkie te fale maja jednakową naturę, a różnią się jedynie długością a co za tym idzie i częstością. W widmie fal elektromagnetycznych można wyróżnić następujące zakresy:

1. Fale radiowe - zakres ten obejmuje fale elektromagnetyczne o długościach od kilku milimetrów do setek kilometrów. Tak więc należą tutaj najdłuższe fale mogą być przesyłane na duże odległości. Zakres fal radiowych dzieli się dodatkowo na fale krótkie, średnie i długie.

Źródłem fal radiowych są specjalne anteny nadawcze. Fale te wykorzystuje się m.in. w radiofonii.

2. Mikrofale - należą tutaj fale o długościach od 1 milimetra do 30 centymetrów. do ich przesyłu stosuje się falowody. mikrofale wykorzystywane są w telekomunikacji satelitarnej, medycynie a także powszechnie używanych kuchenkach mikrofalowych.

3. Promieniowanie podczerwone to promieniowanie o długościach fali od 760 nanometrów do 2000 mikrometrów. Obszar ten dodatkowo dzieli się na trzy rejony: podczerwień bliską, średnią podczerwień i daleką podczerwień. Promieniowanie podczerwone jest odbierane przez narządy zmysłów jako ciepło. Fale z zakresu podczerwieni wykorzystywane są w wielu gałęziach nauki i przemysłu m.in. w analizach chemicznych. Powszechnie używa się tego promieniowania w noktowizorach

4. Światło widzialne to zakres promieniowania elektromagnetycznego, które wywołuje w oku ludzkim wrażenie widzenia.. Są to fale z zakresu od 380 do 780 nanometrów. Zakres ten niekiedy nazywany jest zakresem tęczy, odpowiada bowiem kolorom od czerwieni przez pomarańczowy, żółty, zielony, niebieski aż do fioletowego.

4. Promieniowanie ultrafioletowe - Są to fale z przedziału od 390 do 10 nanometrów. Fale dłuższe, do około 190 nanometrów to ultrafiolet bliski, a fale krótsze to ultrafiolet daleki. Promieniowanie UV emitowane przez Słońce to zarówno UV- A jak i UV-B. promieniowanie ultrafioletowe ma ważną własność. Może mianowicie powodować fluorescencję wielu ciał. Dlatego też z powodzeniem używa się go do wykrywania fałszywych banknotów czy w kryminalistyce przy oględzinach miejsc zbrodni

5. Promieniowanie rentgenowskie to fale z zakresu 12 - 0.012 nanometrów. Dodatkowo obszar ten podzielono na promieniowanie X miękkie i twarde. Promieniami miękkimi nazywa się te , które mają najmniejsze energie. Natomiast promienie twarde to te o energii większej. Promieniowanie rentgenowskie jest bardzo przenikliwe. Promienie X są powszechnie wykorzystywane m.in. w medycynie i przemyśle.

Promieniowanie rentgenowskie powstaje podczas przejścia elektronu w atomie z wyższego poziomu energetycznego na niższy, w którym pozostała luka po wybitym elektronie.

6. Promieniowanie gamma obejmuje fale z zakresu długości
metra. Są to wiec fale najkrótsze. Energie fotonów gamma zawierają się z kolei w przedziale od 10 MeV do 10 KeV. Są to energie wystarczające do wywołania zmian elektrycznych w materii przez która przechodzą. Dlatego też promieniowanie gamma stanowi jeden z przykładów promieniowania jonizującego. Może powstawać w reakcjach rozpadu jąder izotopów promieniotwórczych, w reakcjach syntezy jąder

Emisja promieniowania gamma towarzyszy przejściu jądra pierwiastka promieniotwórczego ze stanu wzbudzonego do stanu o niższej energii.

Promieniowanie gamma należy do najbardziej przenikliwego promieniowania. W przemyśle promieniowanie gamma wykorzystywane jest m.in. do badania metali i ich stopów w celu wykrycia ewentualnych defektów.

Pasmo	Długość [m]
Fale radiowe	>10^-4
Mikrofale	3·10^-1 - 3·10^-3
Podczerwień	10^-3 - 7,8·10^-7
Światło widzialne	7,8·10^-7 - 4·10^-7
Ultrafiolet	4·10^-7 - 10^-8
Promieniowanie rentgenowskie	10^-8 - 10^-11
Promieniowanie gamma	<10^-11

Interferencję fal świetlnych najlepiej ilustruje doświadczenie Younga, przedstawione na rysunku poniżej. Silnym źródłem światła oświetlamy, poprzez czerwony filtr, szczelinę o szerokości około 0,2 - 0,3 mm. W tak otrzymanej wiązce światła umieszczamy układ dwu szczelin. Odległość szczelin nie powinna być większa niż 0,2 - 0,3 mm. Szczeliny te służą do wytworzenia dwu identycznych fal (fal spójnych). Efekt interferencji (nakładania się) fal obserwujemy za pomocą lupy lub okularu mikroskopu (15x).

Interferencja światła jest wynikiem dodawania dwóch promieni świetlnych. Energia elektryczna promienia świetlnego rośnie i maleje na przemian, podobnie jak energia potencjalna w ruchu falowym. Jeśli drgania w dwóch falach są zgodne mówimy, że fale są w fazie. Promienie świetlne są w fazie, gdy w każdym punkcie ich energia elektryczna jednocześnie rośnie albo maleje. Następuje wtedy dodawanie energii i w rezultacie powstaje jeden, jasny promień. O takiej interferencji mówimy, że jest konstruktywna. Jeśli jednak promienie spotykają się w taki sposób, że energia elektryczna jednego z nich rośnie, a drugiego maleje, czyli są w przeciwfazie, wtedy odejmują się wzajemnie. Wynikiem tego odejmowania jest brak światła, czyli ciemne miejsce. Taką interferencję nazywamy destruktywną Interferencja zachodzi dla wszystkich rodzajów fal. W przypadku światła interferencja powoduje powstawanie na przemian jasnych i ciemnych pasm. Skutkiem tego zjawiska są kolory baniek mydlanych. Białe światło odbija się zewnętrznej i wewnętrznej powierzchni bańki. Powstają dwa rozszczepione promienie, które interferują ze sobą tak, że niektóre kolory stają się jaśniejsze, inne przygaszone, zależnie od miejsca.

POLARYZACJA LINIOWA : wektory E są do siebie równoległe we wszystkich punktach fali. Podobnie wektory B.

Mówimy, że ta fala jest płasko spolaryzowana (spolaryzowana liniowo).

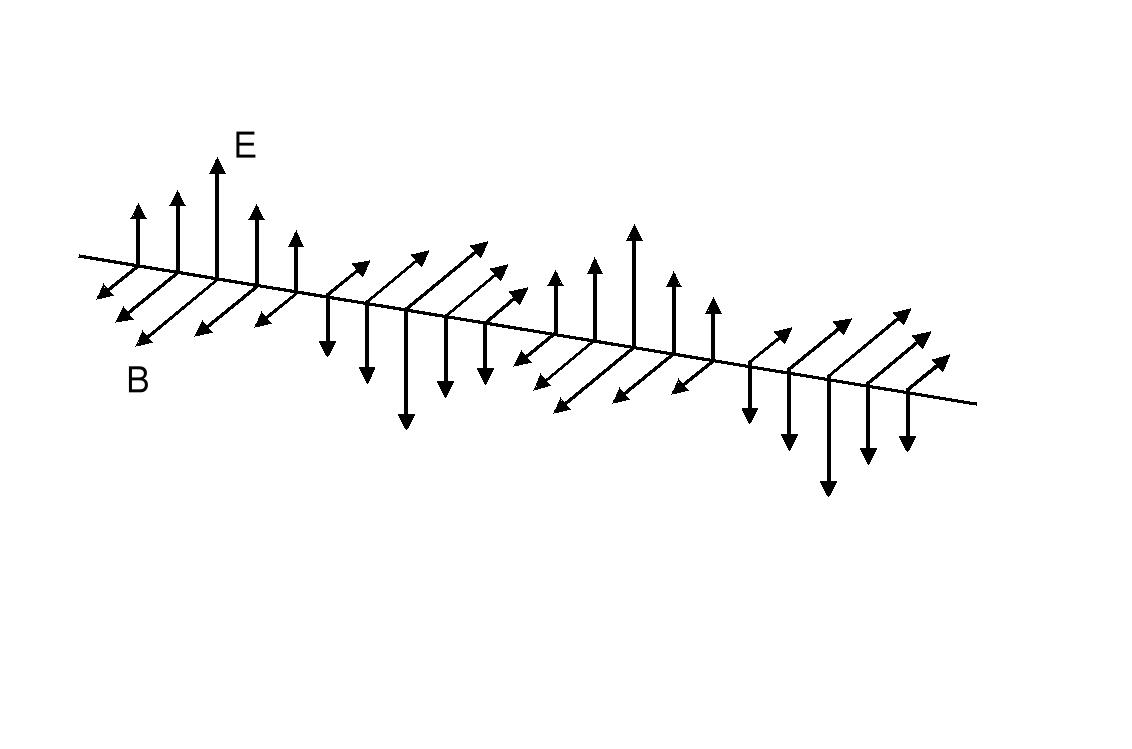
Światło, w którym wektor świetlny E ma jedną płaszczyznę drgań jest światłem spola­ryzowanym liniowo. Wektor świetlny E - Wektor natężenia pola elektrycznego E, którego drgania wywołują wrażenia świetlne Światło liniowo spolaryzowane otrzymuje się poprzez:

1. podwójne załamanie,

2. odbicie od dielektryka,

3. wielokrotne załamanie w dielektryku,

4. dichroizm.

światło może być częściowo lub całkowicie spolaryzowane przez odbicie. Rysunek przedstawia wiązkę niespolaryzowaną padającą na powierzchnię szkła.

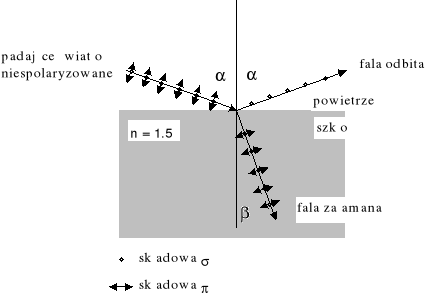
Wektor E można rozłożyć na dwie składowe:

• składową σ prostopadłą do płaszczyzny padania (płaszczyzna rysunku),

• składową π leżącą w płaszczyźnie padania.

Dla światła całkowicie niespolaryzowanego obie składowe maja jednakowe amplitudy.

Stwierdzono doświadczalnie, że dla szkła (i innych materiałów dielektrycznych) istnieje pewien kąt padania, nazywany kątem całkowitej polaryzacji α_p, dla którego współczynnik odbicia składowej π jest równy zero. Wtedy wiązka odbita jest spolaryzowana liniowo prostopadle do płaszczyzny padania. Wiązka przechodząca jest tylko częściowo spolaryzowana (składowa π jest całkowicie załamana, a składowa σ tylko częściowo). Zwróćmy uwagę, że wiązka załamana ma większe natężenie od wiązki odbitej.

Światło podczas odbicia od powierzchni szkła ulega polaryzacji liniowej. Stopień polaryzacji zależy od kąta padania światła na powierzchnię odbijającą. Kąt padania, dla którego światło odbite jest całkowicie spolaryzowane nazywamy kątem Brewstera. Dla szkła kąt ten wynosi około 55^o

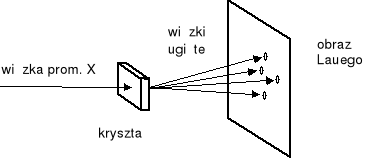
Rysunek poniżej pokazuje wiązkę promieni X, o widmie ciągłym, padającą na kryształ. Wiązki promieni powstałe w wyniku interferencji fal ugiętych na atomach padają na kliszę tworząc na niej charakterystyczny układ punktów zwany obrazem Lauego. Analiza położeń i natężeń tych punktów pozwala na określenie struktury kryształu.

Planck empiryczny wzór opisujący widmową zdolność emisyjną dający wyniki zgodne z doświadczeniem.

Próbując znaleźć taką teorię Planck założył, że atomy ścian zachowują się jak oscylatory elektromagnetyczne, które emitują (i absorbują) energię do wnęki, z których każdy ma charakterystyczną częstotliwość drgań.

Rozumowanie Plancka doprowadziło do przyjęcia dwóch radykalnych założeń dotyczących tych oscylatorów atomowych:

1. Oscylator nie może mieć dowolnej energii, lecz tylko energie dane wzorem

E = nhv

gdzie v oznacza częstość oscylatora, h -stałą (zwaną obecnie stałą Plancka), n - pewną liczbę całkowitą (zwaną obecnie liczbą kwantową).

Z powyższego wzoru wynika, że energia jest skwantowana i może przyjmować tylko ściśle określone wartości. Tu jest zasadnicza różnica bo teoria klasyczna zakładała dowolną wartość energii od zera do nieskończoności.

2. Oscylatory nie wypromieniowują energii w sposób ciągły, lecz porcjami czyli kwantami. Kwanty są emitowane gdy oscylator przechodzi z jednego stanu o danej energii do drugiego o innej energii

ΔE = Δnhv = hv

gdy n zmienia się o jedność.

Dopóki oscylator pozostaje w jednym ze swoich stanów kwantowych (stany stacjonarne) dopóty ani nie emituje ani nie absorbuje energii.

Koncepcja (de Broglie'a) długość fali materii wiąże się bezpośrednio z pędem cząstki. De Broglie nie tylko zaproponował istnienie fal materii ale również przewidział ich długość. Założył, że długość przewidywanych fal materii jest określona tym samym związkiem, który stosuje się do światła.

Analizując zderzenie fotonu z elektronem (efekt Comptona) zastosowano do tego zderzenia zasadę zachowania pędu. Do tych obliczeń potrzebne było wyrażenie na pęd fotonu.

Analogiczne wyrażenie zostało zaproponowane przez de Broglia dla fal materii

Wyrażenie to wiąże teraz pęd cząstki materialnej z długością przewidywanych fal materii.

Zgodnie z równaniem Einsteina dla zjawiska fotoelektrycznego
 energia hν fotonu, w części (W) zostaje zużyta na wyrwanie elektronu z materiału (jego przejście przez powierzchnię), a ewentualny nadmiar energii (hν − W) elektron otrzymuje w postaci energii kinetycznej.

ZJAWISKO FOTOELEKTRYCZNE -polega na uwalnianiu elektronów z różnych materiałów pod wpływem oświetlenia ich powierzchni promieniowaniem o odpowiedniej długości fali (zazwyczaj ultrafioletowym) uwolniony elektron może pozostać we wnętrzu materiału lub też może zostać wyrzucony na zewnątrz w związku z tym rozróżniamy dwa zjawiska fotoelektryczne: zewnętrzne i wewnętrzne . wewnętrzny obserwuje się głównie w półprzewodnikach a jego przejawem jest zmiana oporu elektrycznego i pojawienie się dodatkowego prądu elektrycznego. Efekt zewnętrzny obserwuje się głównie przy oświetlaniu powierzchni metalicznych. Wyrzucenie elektronu na zewnątrz wymaga pokonania sił powierzchniowych na którą zużyta zostaje część energii elektronu.

Proces fotoelektryczny zachodzi zgodnie z zasadą zachowania energii. Energia fotonu zamienia się w prace oraz w energię kinetyczną elektronu, w procesie tym bierze udział tylko 1 foton który w całości absorbowany jest przez elektron. Prędkość elektronu jest tym mniejsza im większa jest długość fali

Zasada nieoznaczoności

iloczyn nieokreśloności pędu cząstki i nieokreśloności jej położenia w danym kierunku jest zawsze większy od stałej Plancka

Ograniczenie to wyrażają nierówności

Zauważmy, że im dokładniej mierzymy pęd, np. zmniejszamy Δp_x, tym bardziej rośnie nieoznaczoność położenia Δx.

Druga część zasady nieoznaczoności dotyczy pomiaru energii i czasu potrzebnego na wykonanie tego pomiaru.

	Jeżeli cząstka posiada energię E, to dokładność jej wyznaczenia ΔE zależy od czasu pomiaru  Δt zgodnie z relacją

Im dłużej cząstka jest w stanie o energii E tym dokładniej można ją wyznaczyć.

Δp_yΔy ≅ h

Jeżeli chcemy poprawić pomiar y (zmniejszyć Δy) to w wyniku zmniejszenia szerokości szczeliny otrzymujemy szersze widmo dyfrakcyjne (mocniejsze ugięcie). Inaczej mówiąc zwiększone zostało Δp_y. Równani to przedstawia ograniczenie nałożone na dokładność pomiarów przez przyrodę (nie ma nic wspólnego z wadami aparatury pomiarowej).

Równanie to jest szczególnym przypadkiem ogólnej zasady podanej przez W. Heisenberga znanej jako zasada nieoznaczoności.

W zastosowaniu do pomiaru pędu i położenia głosi ona, że

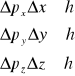
Tak więc żadna składowa ruchu elektronu nie może być określona z nieograniczoną dokładnością. Ta sama zasada obowiązuje w odniesieniu do energii i czasu.

Zasada nieoznaczoności Heisenberga głosi, w zastosowaniu do pomiarów pędu i położenia, że iloczyn nieokreśloności pędu cząstki i nieokreśloności jej położenia w danym kierunku jest zawsze większy od stałej Plancka np.
. Druga część zasady nieoznaczoności dotyczy pomiaru energii i czasu i stwierdza, że jeżeli cząstka posiada energię E, to dokładność jej wyznaczenia ΔE zależy od czasu pomiaru  Δt zgodnie z relacją

Atomy ułożone są w powtarzający się regularny wzór zwany siecią krystaliczną. Ze względu na typy wiązań kryształy dzielimy na:

• Kryształy cząsteczkowe (molekularne);

• Kryształy o wiązaniach wodorowych;

• Kryształy jonowe;

• Kryształy atomowe (kowalentne);

• Kryształy metaliczne.

Wiązania molekularne: Składają się ze stabilnych cząsteczek, które zachowują wiele swoich cech indywidualnych nawet przy zbliżaniu ich do siebie. Energia wiązania jest słaba Te kryształy są podatne na odkształcenia (słabe wiązanie) oraz ze względu na brak elektronów swobodnych są bardzo złymi przewodnikami ciepła i elektryczności

równanie Schrödingera. Jest to równanie różniczkowe opisujące zachowanie się układu kwantowego w czasie i przestrzeni, które w szczególności przyjmuje postać

(35.4)

gdzie E jest energią całkowitą cząstki, U(x) jej energią potencjalną zależną od jej położenia, a
.

Zależność (35.4) przedstawia najprostszą formę równania Schrödingera to jest równanie w jednym wymiarze i niezależne od czasu.

Rozwiązanie równania Schrödingera polega na znalezieniu postaci funkcji falowej ψ i wartości energii cząstki E przy znanej działającej na cząstkę sile zadanej poprzez energię potencjalną U.

METODY OTZRYMYWANIA PROMIENI X -powstają przy hamowaniu wiązek elektronowych przyśpieszonych uprzednio w polu elektrycznym o napięciu kilkadziesiąt tysięcy woltów w lampie próżniowej. powstają również w wyniku wzbudzeń atomów zachodzących na głębokich powłokach elektronów ciężkich atomów. Standardową metodą otzrymywania promieni rentgenowskich jest specjalna lampa próżniowa

T e r m i n o l o g i a   t e o r i i   f a l o w e j

 T e r m i n o l o g i a   t e o r i i   k w a n t ó w

Światło jednorodne ma określoną długość fali. Długość fali jest dla czerwonego krańca widma dwa razy większa niż dla krańca fioletowego.

Światło jednorodne zawiera fotony o określonej energii. Energia fotonu jest dla czerwonego krańca widma dwa razy mniejsza niż dla krańca fioletowego.

Obecny stan rzeczy możemy podsumować, jak następuje: istnieją zjawiska, które można wytłumaczyć, posługując się teorią kwantów, a nie można, używając teorii falowej. Przykładem może być zjawisko fotoelektryczne, choć znane są i inne takie zdarzenia. Istnieją zjawiska, które można wytłumaczyć za pomocą teorii falowej, a nie można za pomocą teorii kwantów. Typowym przykładem jest tu uginanie się światła na przeszkodach. Istnieją wreszcie zjawiska, jak na przykład prostoliniowe rozchodzenie się światła, które można wytłumaczyć równie dobrze, posługując się kwantową teorią światła, jak i teorią falową.

Potencjał nieskończenie głębokiej prostokątnej studni ma tę własność, że wiąże cząstkę o skończonej energii . W mechanice klasycznej dozwolona jest dowolna wartość energii,

natomiast w mechanice kwantowej dozwolone są tylko pewne dyskretne wartości własne . Dla niezbyt dużych wartości liczby kwantowej n odpowiadające im wartości własne i funkcje własne użyte być mogą jako przybliżenie odpowiadających im wartości własnych i funkcji własnych dla potencjału o dużym, lecz skończonym

zależność oporności od temperatury:

metale: ze wzrostem temperatury maleje ruchliwość i przewodność metali zwiększa się ich oporność

półprzewodniki: ze wzrostem temperatury zwieksza się łączna liczba elektronów swobodnych i maleje opór elektryczny półprzewodnika

działanie diody i tranzystora

Działanie diody - przewodzi ona prąd tylko w jednym kierunku. Jeśli potencjał anody jest większy od potencjału katody dioda przewodzi prąd. W przeciwnym przypadku nie.

Działa jak jednokierunkowy zawór - przepuszcza tylko w jedną stronę

Działanie tranzystora : Wyróżnia się dwa zasadnicze rodzaje tranzystorów typu n-p-n i p-n-p. W tranzystorach n-p-n pierwszy z obszarów n połączony jest ze stykiem nazywanym emiterem (w bezpośrednim sąsiedztwie styku znajduje się duża koncentracja domieszek), obszar p z tzw. bazą, a drugi obszar n z tzw. kolektorem. Działanie tranzystora polega na tym, że prąd płynący z emitera do kolektora sterowany jest przez prąd bazy.

---