Adam Mizera środa, 23 lutego 2000

I rok fizyki

Ćwiczenie nr 15

Badanie drgań wahadła sprężystego

Lp.	Amplituda [cm]	Czas [s]
1	1	21,2
2	2	22
3	3	21,6
4	4	22,1
5	5	21,7
6	6	22,5
7	7	22,1
8	8	21,8
9	9	21,7
10	10	21,7

Lp.	Obciążenie [g]	Czas [s]
1	40	20
2	50	21,6
3	60	22,5
4	70	23,9
5	80	25,3
6	90	26,2
7	100	27,6
8	mx	22

Lp.	Obciążenie [g]	Wyd. spręż. [cm]
1	10	3,5
2	20	7
3	30	10,5
4	40	14
5	50	17
6	60	20,5
7	70	24
8	80	27,5
9	90	30,5
10	100	34

Prawo Hooke'a.

Przyrost długości
, jakiego doznaje ciało sprężyste przy rozciąganiu siłą F jest wprost proporcjonalny do wielkości tej siły i do długości początkowej ciała
, a odwrotnie proporcjonalny do jego przekroju poprzecznego S. Ponadto przyrost długości jest zależny od rodzaju materiału, z którego wykonane jest ciało. Zależność tę ujmuje liczbowo współczynnik proporcjonalności k.

W tablicach własności wytrzymałościowych materiałów podaje się najczęściej odwrotność współczynnika k, zwaną modułem sprężystości podłużnej E lub modułem Younga.

Stosunek wielkości siły rozciągającej F do wielkości przekroju poprzecznego S odkształcanego ciała nazywamy naprężeniem
. Liczbowo określa ono wielkość siły przypadającej na jednostkę przekroju poprzecznego odkształcanego ciała

Wprowadzając pojęcie naprężenia do równania Hooke'a otrzymamy następującą jego postać:

stąd

Stosunek
nosi nazwę wydłużenia względnego. Wynika stąd, że wydłużenie względne przy rozciąganiu jest wprost proporcjonalne do wartości naprężenia

.

Ruch harmoniczny.

Ruch, który powtarza się w regularnych odstępach czasu, nazywamy ruchem okresowym (periodycznym). Przemieszczenie cząstki w takim ruchu można zawsze wyrazić przy pomocy funkcji sinus i cosinus. Ruch periodyczny często nazywamy ruchem harmonicznym.

Okresem ruchu harmonicznego jest czas trwania jednego pełnego drgnięcia, to jest czas powtarzania się każdego pełnego przemieszczenia albo cyklu.

Częstością ruchu
jest liczba drgań (albo cykli) na jednostkę czasu. Zatem częstość jest po prostu odwrotnością okresu, czyli

.

Położeniem równowagi w ruchu drgającym nazywamy położenie, w którym na punkt materialny nie działa siła wypadkowa. Przemieszczenie (linowe albo kątowe) jest to odległość (liniowa albo kątowa) drgającego punktu materialnego od położenia równowagi w dowolnej chwili.

Przemieszczenie drgającego punktu materialnego x zmienia się okresowo, zarówno co do wartości, jak i kierunku. Jego prędkość v i przyśpieszenie a także zmieniają się okresowo co do wartości i kierunku. Biorąc pod uwagę zależność F=ma, również siła F działająca na punkt materialny zmienia się okresowo.

Wahadło sprężynowe.

Ruch harmoniczny obserwujemy nie tylko w przypadku wahadła matematycznego, gdzie drganie odbywa się pod wpływem siły ciężkości, ale również w przypadku występowania sił oporu sprężystego, np. przy odkształceniach sprężystych. Wahadło, które drga pod wpływem sił oporu sprężystego, nazywamy wahadłem sprężynowym. Przykładem takiego wahadła może być kulka zawieszona na sprężynie, której drugi koniec jest przytwierdzony do nieruchomego statywu. Jeżeli odciągniemy kulkę z położenia równowagi, to wskutek deformacji sprężyny pojawi się siła oporu sprężystego, skierowana do środka równowagi. Jeśli wtedy puścimy kulkę to zacznie się ona poruszać do punktu równowagi, wskutek bezwładności minie go i zatrzyma się na chwilę w innym punkcie tak samo odległym od położenia równowagi jak ten z którego ruch się rozpoczął. W tym położeniu sprężyna będzie również zdeformowana. Siła oporu sprężystego jest zawsze skierowana przeciwnie niż kierunek deformacji, to znaczy skierowana ku środkowi równowagi. Kulka będzie się więc znowu poruszała w kierunku położenia równowagi, minie go wskutek bezwładności i osiągnie punkt z którego ruch się rozpoczął, gdzie zmieni swój kierunek itd.; drga więc ona ruchem harmonicznym między punktami zwrotnymi. Siłą, która ten ruch wywołuje, jest siła oporu sprężystego. Zgodnie z prawem Hooke'a dla niewielkich odkształceń, a z takimi mamy tu do czynienia, słuszna jest zależność

,

gdzie x oznacza wydłużenie sprężyny równe wychyleniu punktu drgającego, a k oznacza współczynnik proporcjonalności. Znak „-” oznacza, że siła F ma kierunek odwrotny niż wychylenie x.

Z powyższego równania otrzymujemy

.

Na podstawie tej zależności można powiedzieć, że k oznacza siłę powodującą wychylenie x równe jednostce np. 1 cm . Jest to tzw. siła kierująca.

Z rozważań nad ruchem harmonicznym wiadomo, że siłę wywołującą go można wyrazić zależnością

.

Porównując prawe strony równań pierwszego i trzeciego otrzymujemy

,

skąd

.

Jak widać z powyższych rozważań, amplituda drgań nie występuje wcale w końcowym wzorze; jest to zgodne z faktem, że okres drgań wahadła sprężynowego nie zależy od amplitudy. Wniosek ten, sprawdzany doświadczalnie nawet w odniesieniu do dość dużych wychyleń, stanowi treść prawa izochronizmu drgań wahadła sprężynowego.

Opracowanie wyników pomiarów

1) Okresem ruchu harmonicznego jest czas trwania jednego pełnego drgnięcia, to jest czas powtarzania się każdego pełnego przemieszczenia albo cyklu.

T₁= 21,2 [s] / 20 = 1,06 [s]

T₂= 1,10 [s]

T₃= 1,08 [s]

T₄= 1,10 [s]

T₅= 1,09 [s]

T₆= 1,12 [s]

T₇= 1,10 [s]

T₈= 1,09 [s]

T₉= 1,08 [s]

T₁₀= 1,08 [s]

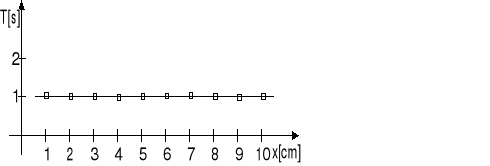
2) Siła ciężarka działająca na sprężynę jest równa F=mg gdzie m - masa ciężarka g- przyspieszenie ziemskie, a siła kierująca wynosi k=F/x.

F₁=m₁g=10[g]*9,81[m/s²]=0,01[kg]*9,81[m/s²]=0,0981[N]

k₁=F₁/x₁=0,0981/0,035=2,803

F₂=0,02*9,81=0,1962 [N] F₃=0,03*9,81=0,2943 [N]

k₂=0,1962/0,07=2,803
k₃=0,2943/0,105=2,803

F₄=0,04*9,81=0,3924 [N] F₅=0,05*9,81=0,4905 [N]

k₄=0,3924/0,14=2,803
k₅=0,4905/0,17=2,885

F₆=0,06*9,81=0,5886 [N] F₇=0,07*9,81=0,6867 [N]

k₆=0,5886/0,205=2,871
k₇=0,6867/0,24=2,861

F₈=0,08*9,81=0,7848 [N] F₉=0,09*9,81=0,8829 [N]

k₈=0,7848/0,27=2,91
k₉=0,8829/0,305=2,895

F₁₀=0,1*9,81=0,981 [N] k₁₀=0,981/0,34=2,885

Średnia wartość k wynosi

3) Okresy oraz ich kwadraty dla poszczególnych mas obliczam według metody z punktu 1.

T₁=1 [s] T₁²=1 [s]

T₂=1,08 [s] T₂²=1,17 [s]

T₃=1,25 [s] T₃²=1,27 [s]

T₄=1,19 [s] T₄ ²=1,42 [s]

T₅=1,26 [s] T₅²=1,61 [s]

T₆=1,31 [s] T₆²=1,72 [s]

T₇=1,38 [s] T₇²=1,91 [s]

T_x=1,1 [s] T_x²=1,21 [s]

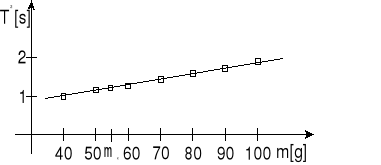
Masa m_x odczytana z wykresu wynosi ponad 50 [g].

Natomiast masa m_x wyliczona ze wzoru wynosi:

Tak duża rozbieżność może wynikać z błędu grubego popełnionego przy pomiarze, który był wykonywany tylko raz więc nie można było go porównać z innymi wynikami.

Rachunek błędu:

Wykonujemy metodą różniczki zupełnej.

W punkcie pierwszym mieliśmy:

, gdzie t jest czasem trwania ruchu mierzonym w sekundach, a n jest ilością wykonanych wahnięć w tym czasie. W naszym przypadku n jest stałe (wynosi 20), więc traktujemy je jako stałą bez błędu.

,
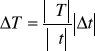
natomiast błąd pomiaru czasu Δt=0,1 [s].

Stąd błąd każdego pomiaru jest stały i wynosi:

Błąd względny:

W punkcie drugim mamy:

, w tym przypadku F jest siłą, której nie mierzymy, więc również możemy ją przyjąć jako bez błędu.

,
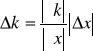
a błąd Δx = 0,001 [m], stąd błędy poszczególnych sił kierujących wynoszą:

Δk₂=0,04
Δk₃=0,027

Δk₄=0,02
Δk₅=0,017

Δk₆=0,014
Δk₇=0,012

Δk₈=0,011
Δk₉=0,009

Δk₁₀=0,008

Średni błąd siły kierującej k:

0,08+0,04+0,027+0,02+0,017+0,014+0,012+0,011+0,009+0,008=0,238

Błąd względny:

Błąd maksymalny siły kierującej obliczam ze wzoru:

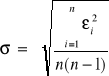
gdzie
i n to ilość pomiarów.

Podstawiając kolejne wartości do wzoru otrzymałem:

ki	kśr	ၥi^2
0,0801	0,238	0,024932
0,04	0,238	0,039204
0,027	0,238	0,044521
0,02	0,238	0,047524
0,017	0,238	0,048841
0,014	0,238	0,050176
0,012	0,238	0,051076
0,011	0,238	0,051529
0,009	0,238	0,052441
0,008	0,238	0,0529

Stąd
, więc błąd maksymalny wynosi σ = ±0,002573
.

Wnioski:

Wykonane obliczenia i wykresy pozwalają stwierdzić, że prawo izochronizmu wahadła sprężynowego zostało zachowane. Jedynie błąd przy wyznaczaniu nieznanej masy m_x jest zbyt duży co sugeruje, że popełniono gruby błąd przy pomiarach okresu dla tej masy co spowodowało tak duże rozbieżności.

---