Kuziel Paweł	WEAiI kierunek Elektrotechnika	Grupa:101B	Zespół: 1
Ćwiczenie nr: O5	Wyznaczanie stałej siatki dyfrakcyjnej.
Data: 30.V.2006r.	Ocena:

1.Wstęp teoretyczny:

Siatką dyfrakcyjną nazywamy szereg szczelin umieszczonych w różnych od siebie odległościach na nieprzeźroczystym ekranie. W praktyce siatkę dyfrakcyjną otrzymuje się najczęściej przez porysowanie płytki szklanej za pomocą diamentu szeregiem równoległych kresek. Nieprzeźroczyste rysy spełniają rolę zasłon, a przestrzenie między nimi to szczeliny.

Światło padające na siatkę dyfrakcyjną doznaje ugięcia na każdej szczelinie. Zgodnie z zasadą Huygansa każda szczelina staje się źródłem drgań i wysyła promienie we wszystkich kierunkach , a więc nie tylko w kierunku promieni padających. Zjawisko to nazywa się dyfrakcją, czyli uginaniem prostoliniowego bieg promieni . promienie ugięte mogą nakładać się , czyli interferować ze sobą gdyż są promieniami spójnymi : znaczy to że różnice faz między nimi zależą tylko od różnic dróg geometrycznych , nie zależą zaś od czasu. Biorąc pod uwagę wiązki promieni ugiętych zauważyć można , że w pewnych kierunkach promienie te będą się wzmacniały, w innych zaś wygasały . promienie ugięte będą się wzmacniać, jeśli różnice dróg dwóch sąsiednich promieni będą równe całkowitej wielokrotności długości światła padającego.

Kierunek wzmocnienia promieni ugiętych na siatce dyfrakcyjnej ma postać:

gdzie:

d- odległość między szczelinami (stała siatki)

n- rząd widma (n=1,2,3,...)

- długość fali

- kąt ugięcia promieni

Przy każde wartości długości fali
, oraz przy każdym „n” , kąt wzmocnienia się promieni ugiętych jest inny, a więc kierunki wzmocnienia promieni różnych barw są różne . W wyniku tego obserwujemy następujące zjawisko: jeżeli poza siatką dyfrakcyjną , na którą pada wiązka promieni równoległych umieścimy soczewkę zbierającą , a w pewnej odległości ekran - to powstaną na nim oprócz smugi odpowiadającej promieniom nie ugiętym po jej obu stronach barwne widma . Maksima promieni ugiętych są szczególnie wyraźne , gdy wzmacniają się promienie wychodzące ze wszystkich szczelin.

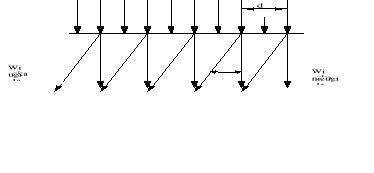
Rys: ugięcie promieni na siatce dyfrakcyjnej.

2.Przebieg ćwiczenia:

Część pierwsza:

Pierwsza część ćwiczenia zakłada wyznaczenie stałej siatki dyfrakcyjnej za pomocą lasera He - Ne. Laser ten jest bardzo dobrym źródłem światła do badania interferencji i dyfrakcji ponieważ daje wiązkę światła spójną , równoległą i monochromatyczną o długości fali
=632,8nm. Aby określić stałą siatki aparaturę ustawiamy wg. schematu:

Ponieważ znamy wartości :
,n, x - odległość prążka od środka ekranu, oraz l - odległość siatki dyfrakcyjnej od ekranu możemy obliczyć stałą siatki dyfrakcyjnej z zależności :

Pomiary wykonujemy dla dwóch odległości siatki od ekranu , oraz dla dwóch rzędów widm światła laserowego.

Część druga:

W drugiej części ćwiczenia należy dokonać pomiaru długości fal światła lampy rtęciowej . przyrządy należy ustawić wg schematu:

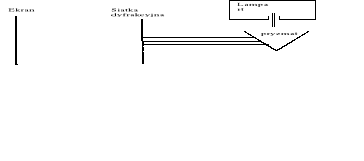
Aby obliczyć długość fali światła padającego na siatkę dyfrakcyjną korzystamy z zależności:

Aby móc wykonać te obliczenia musimy znać stałą siatki „d” , którą wyznaczamy w pierwszej części ćwiczenia . Pomiary wykonać dla trzech wybranych prążków dyfrakcyjnych dla dwóch rzędów widma. Pomiary powtarzamy dla dwóch odległości siatki dyfrakcyjnej od ekranu.

3.Wyniki pomiarów:

x[mm]	l[mm]	rząd	[ m]	[ m]
67 136	500 500	I II	4,764597 0,000047 4,821992 0,000045	0,6328
105 217	800 800	I II	4,862684 0,000048 4,834407 0,000045	0,6328

x[mm]	l[mm]	rząd
Fioletowy 45 Zielony 57 Żółty 60	500 500 500		I I I	0,432136 0,004781 0,546048 0,004661 0,580425 0,004782
Fioletowy 92 Zielony 117 Żółty 124	500 500 500		II II II	0,436202 0,004664 0,549212 0,004578 0,580217 0,004564
Fioletowy 71 Zielony 90 Żółty 96	800 800 800		I I I	0,426182 0,004760 0,538954 0,004569 0,580425 0,004752
Fioletowy 145 Zielony 185 Żółty 197	800 800 800		II II II	0,429892 0,004354 0,543078 0,004751 0,576358 0,004536

Obliczenia: Obliczam stałą siatki dyfrakcyjnej:

m

Jako wartość stałej siatki dyfrakcyjnej przyjmuję średnią ze wszystkich pomiarów:

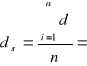
4,82092

Obliczam długości fal światła lampy rtęciowej:

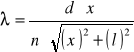
• fioletowa:

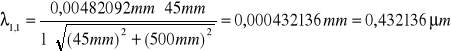
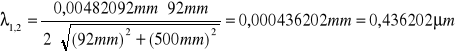
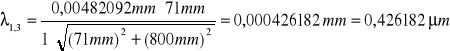
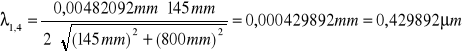
• zielona:

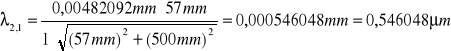
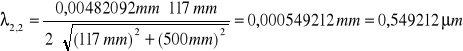
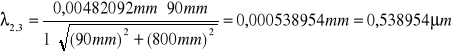
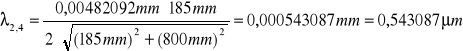
• żółta:

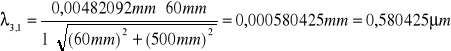
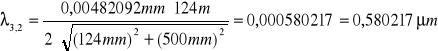
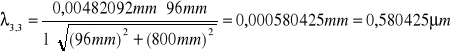
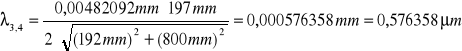
ocena błędów:

l =
1mm

x =
1mm

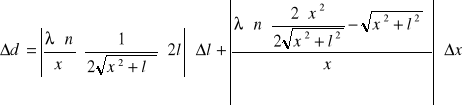
d₁=0,000047

d₂=0,000045

d₃=0,000048

d_śr=0,000046

d₄=0,000045

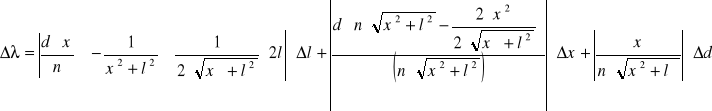
₁=0,004781

₂=0,004661

₃=0,004782

₄=0,004664

₅=0,004578

₆=0,004564

₇=0,004760

₈=0,004569

₉=0,004752

₁₀=0,004354

₁₁=0,004751

₁₂=0,004536

3

laser

Siatka

dyfrakcyjna

ekran

Widma I-ego rzędu

Widma II-ego rzędu

---