„WAHADŁO MATEMATYCZNE”

WPROWADZENIE

Celem ćwiczenia jest wyznaczenie przyspieszenia ziemskiego.

Przy założeniu braku sił oporu powietrza wartość tego przyspieszenia na powierzchni Ziemi wynosi:

gdzie: G- stała grawitacji

M- masa Ziemi

R- promień Ziemi

Na każde ciało znajdujące się na Ziemi działa siła Coriolisa, jest ona związana z różnymi prędkościami liniowymi na różnych szerokościach geograficznych. Do obliczania zależności przyspieszenia ziemskiego od szerokości geograficznej stosuje się empiryczny wzór Hayforda:

Najprostszą metodą pomiaru przyspieszenia ziemskiego jest pomiar czasu spadku swobodnego. Przy tej metodzie uwzględnić trzeba jednak szereg poprawek typu opór powietrza. Do precyzyjnego pomiaru stosuje się tzw. grawimetry. Ich działanie polega na porównaniu siły ciężkości z siłą sprężystą. Dzielimy je na grawimetry gazowe, kwarcowe i metalowe. Dokładność tej aparatury sięga 1 cm/s².

Do naszych badań używamy wahadła prostego, które jest odwzorowaniem modelowego wahadła matematycznego. Składa się ono z metalowej kulki zawieszonej na nierozciągliwej nici.

Składowa styczna siły ciężkości wyraża się wzorem:

Dla małych wychyleń można przyjąć, że:

Przyspieszenie styczne do toru kuli jest równe:

Z drugiej zasady dynamiki otrzymujemy:

Jest to równanie ruchu harmonicznego prostego, a jego rozwiązaniem jest funkcja:

gdzie:

*_m - amplituda drgań

*₀ - faza początkowa

* -częstość równa

T- okres drgań wahadła równy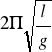

PREBIEG ĆWICZENIA

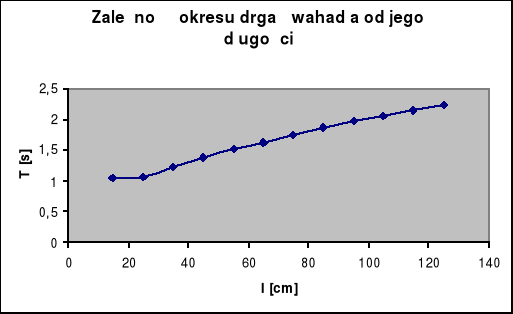
1. Zmierzyliśmy czasy 10 wahnięć wahadła dla długości ramienia 15-125 cm zmieniając ją co 10 cm

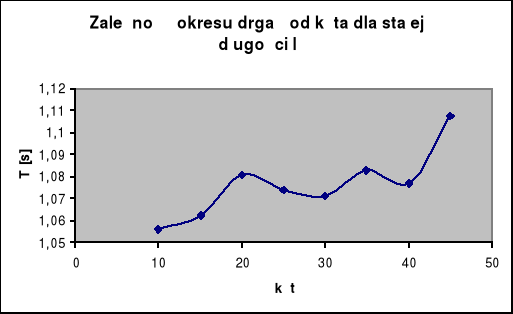
2. Zmierzyliśmy czasy 10 wahnięć wahadła dla różnych jego wychyleń 45^o-10^o zmieniając co 5^o.

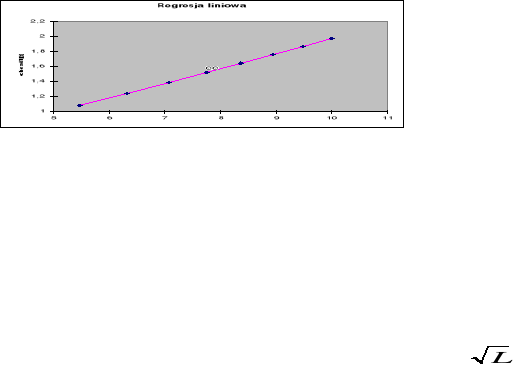
3. Przeprowadziliśmy regresję liniową do pkt-u 1 gdzie y=T, x=
   

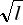
4. Wykreśliliśmy zależność T(*)

5. Z otrzymanych wyników obliczyliśmy przyspieszenie ziemskie za wzoru
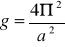
   oraz jego błąd ze wzoru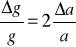
   

TABELA POMIAROWA

L [cm]	10T [s]	T [s]
15	10,44	1,044
25	10,75	1,075
35	12,30	1,230
45	13,87	1,387
55	15,21	1,521
65	16,33	1,633
75	17,55	1,755
85	18,78	1,878
95	19,68	1,968
105	20,59	2,059
115	21,55	2,155
125	22,37	2,237

Błędy pomiaru: *L=0,2[cm] *(20T)=1[s] *T=0,05

Regresja liniowa dla zależności: y=ax+b gdzie y=t x=

a=0,896 +- 0,030 [m/s] b=0,60 +- 0,25 [s]

Zależność od kąta dla stałej długości L = 30 [cm]

*[^o]	10T [s]	T[s]
45	11,08	1,108
40	10,77	1,077
35	10,83	1,083
30	10,71	1,071
25	10,74	1,074
20	10,71	1,071
15	10,62	1,062
10	10,56	1,056

Błędy pomiaru: *L=0,2[cm] **=1[^o] *(10T)=1[s] *T=0,2[s]

OBLICZENIA

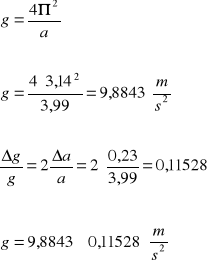
WNIOSKI

Wyliczona przez nas wartość g zgadza się w granicach błędu z wartością tablicową. Błąd jest spowodowany niedokładnym ustawieniem długości wahadła, niedokładnym pomiarem czasu (pomiar był robiony za pomocą stopera, a nie fotokomórki oraz niedokładnością ludzkiego oka)

1

4

---