Numer ćwiczenia: 3		Temat: Wyznaczanie przyspieszenia ziemskiego za pomocą wahadła matematycznego.
ZIP 1 rok dzienne
Data wykonania:	Data oddania:	Ocena:

1. Wstęp teoretyczny

Przyspieszenie ziemskie g jest to przyspieszenie, jakie nadaje siła ciężkości swobodnie spadającemu ciału, czyli siła, z jaką Ziemia przyciąga to ciało. Wartość g nie jest stała. Maleje w miarę jak rośnie wysokość. Wartość przyspieszenia zależy też od położenia punktu na powierzchni Ziemi.

Wahadło matematyczne jest jednym ze sposobów wyznaczania przyspieszeni ziemskiego, jest to punkt materialny, zawieszony na długiej, nieważkiej i nierozciągliwej nici znajdujący się w polu ciężkości.. Wahadło, wychylone o mały kąt z położenia równowagi, wykonuje ruch drgający prosty. Jest to ruch ciała zachodzący wokół stałego położenia równowagi. W przypadku ruchu okresowego położenie lub stan ciała powtarza się w jednakowych odstępach czasu ( = okres drgań T). Przyspieszenie ruchu wahadła w przypadku małych jego wychyleń (do 5^o) jest proporcjonalne do wychylenia punktu materialnego z położenia równowagi i skierowane ku temu położeniu. W takiej sytuacji okres wahań wynosi:

gdzie:

l - długość wahadła

g - przyspieszenie ziemskie

2. Przebieg doświadczenia

Celem doświadczenia jest wyznaczenie przyśpieszenia ziemskiego za pomocą wahadła matematycznego

Kroki :

1.

Mierzymy długość nici od punktu zawieszenia do połowy kuli

2. Wykonujemy 3 pomiary średnicy kulki za pomocą suwmiarki.

3.

Wychylamy wahadło około 4 cm od położenia równowagi.

4. Za pomocą stopera mierzymy czas 20 pełnych wahnięć.

5. Pomiary wpisujemy do tabeli.

Potrzebne przyrządy:

Statyw; niewielka metalowa kulka, zawieszona na długiej, nierozciągliwej nici; suwmiarka, metr; stoper.

3.Wyniki i opracowania

lp	Śr.kulki	Długość nici	Czas okresów 20		Okres T		Śr. Wartość T	g
1	0,03	1,535	49,176		2,459		2,462	10,01
2	0,03	1,535	49,264		2,463				9,98
3	0,03	1,535	49,279		2,464				9,97
4	0,02	2,029	56,586		2,829			2,838	10,00
5	0,02	2,029	56,781		2,839				9,93
6	0,02	2,029		56,910		2,846			9,88

Obliczam T:

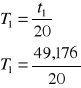
T₁ = 2,459s

I tak obliczamy dla kolejnych:

T₂ = 2,463 s

T₃ = 2,464s

T₄ = 2,829s

T₅ = 2,839s

T₆ = 2,846s

Obliczam g :

g₁ = 10,01m/s²

i obliczamy dla wszystkich wyników

g₂ = 9,98 m/s²

g₃ = 9,97 m/s²

g₄ = 10,00 m/s²

g₅ = 9,93m/s²

g₆ = 9,88m/s²

Obliczam g':

g'=g

g₁ = 10.01m/s²

g₂ = 9,98 m/s²

g₃ = 9,97 m/s²

g₄ = 10,00 m/s²

g₅ = 9,93m/s²

g₆ = 9,88m/s²

Obliczamy średni błąd kwadratowy Δg`, ponieważ g`=g.

Lp.	g` [m/s^2]	ε	ε^2	εśr^2
1.	10,01	0,02	0,0004	0,0003
2.	9,98	-0,01	0,0001
3.	9,97	-0,02	0,0004
4.	10,00	0,06	0,0036		0,0024
5.	9,93	-0,01	0,0001
6.	9,88	-0,06	0,0036

Obliczenia:

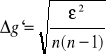
n - liczba pomiarów

ε= g`- g`_śr

g`_śr=9,99 m/s²

g`_śr = 9,94m/s²

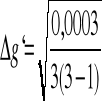
 g'= 0,007 m/s²

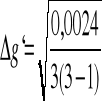
 g'= 0,0004 m/s²

^{Bezwzględny błąd pomiarowy:}

^{Δl = 0,001m}

^ΔT=0,02s

Względny błąd pomiarowy:

|Δg / g| = |Δl / l| + 2 |ΔT / T|

|Δg / g| = |0,001 / 1,535| + 2 |0,02 / 2,462| = | 0,0163|

|Δg / g| = |0,001 / 2,029| + 2 |0,02 / |2,838= | 0,0140|

Δg = ± |9,99· | 0,0163| m / s2

Δg = ± |9,94· | 0,0140| m / s2

Δg= ± |0,163| m / s2

Δg= ± |0,139| m / s2

9,99±0,163 m / s2

9,94±0,139 m / s2

Wnioski:

Za pomocą wahadła matematycznego udało nam się dość dokładnie zmierzyć wartość przyspieszenia ziemskiego. Nie dysponowaliśmy bardzo dobrym sprzętem, dlatego otrzymany przez nas wynik nie jest bardzo dokładny. Błędy pomiarowe wynikają z trudności w uchwyceniu momentu, kiedy wahadło kończy swoje drganie.

Podczas pomiarów zauważyliśmy również, że okres drgań nie zależy od tego, jak bardzo wychyla się wahadło. Jest to zgodne z wzorem, który napisaliśmy we wstępie.

2

2

1

2

2

2,459

1,535

,

1

)

14

,

3

(

4

4









g

T

l

g



---