Nr ćw. 3	Temat: WAHADŁO MATEMATYCZNE
Rok i kierunek ZARZĄDZANIE I INŻYNIERIA PRODUKCJI			Imię i nazwisko
Wykonane 27.10.2008r		Data oddania 03.11.2008r		Ocena:

1. Wstęp teoretyczny

Przyspieszenie ziemskie (przyspieszenie spadku swobodnego na Ziemi) g, jest to przyspieszenie w próżni nadawane przez siłę grawitacyjną Ziemi ciału znajdującemu się na jej powierzchni. Wartość przyspieszenia ziemskiego zależy od szerokości geograficznej oraz wysokości nad poziomem morza. Przyśpieszenie ziemskie na szerokości geograficznej 45^o i poziomie morza wynosi w przybliżeniu:

Z prawa powszechnej grawitacji można wyliczyć, że na powierzchni Ziemi jego wartość dana jest wzorem:

gdzie: G - siła grawitacji

M - masa Ziemi

T - promień Ziemi

Wahadło matematyczne jest to punkt materialny zawieszony na nierozciągliwej i nieważkiej nici. Jest to idealizacja wahadła fizycznego. Ważną cechą wahadła fizycznego i matematycznego jest stałość okresu drgań dla niewielkich wychyleń wahadła.

l - długość wahadła

x - wychylenie wahadła z położenia równowagi

β - kąt wychylenia

Jeżeli kąt jest niewielki (β<5⁰) to ruch naszego układu możemy traktować jako ruch harmoniczny, i po odpowiednich przekształceniach otrzymujemy okres drgań który dany jest wzorem:

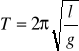
gdzie:

l - długość wahadła

g - przyspieszenie ziemskie

Jak wykazuje wzór, okres wahań wahadła matematycznego zależy od:

- długości wahadła,

- wartości przyspieszenia ziemskiego.

Dzięki wyznaczonemu wzorowi na okres drgań wahadła możemy łatwo wyznaczyć wzór na przyspieszenie ziemskie g:

2. Przebieg doświadczenia

Po zawieszeniu metalowej kulki na cienkiej, nierozciągliwej nici o długości około 2 m przeprowadzamy pomiar średnicy kulki, długości nici a w końcowym rezultacie długości wahadła. Dokonawszy pomiaru długości wahadła odchylamy kulkę od położenia równowagi o kąt nie większy niż 5^o i obserwujemy wahania. By dokładnie wyznaczyć T, mierzymy czas 20 okresów, a następnie otrzymujemy czas jednego pełnego wahnięcia. Pomiary te powtarzamy trzykrotnie. Tak samo postępujemy po zmianie długości wahadła. Pomiary powtarzamy dla trzech długości wahadła a wyniki wpisujemy odpowiednio do tabel.

3. Opracowanie wyników

Pomiar 1
Lp.	Średnica kuli [m]	Długość nici [m]	Długość wahadła [m]	Czas 20 okresów [s]	Okres T [s]	Średnia Wartość T [s]	g
1.	0,030	1,324	1,339	46,242	2,312	2,318	9,838
2.	0,030	1,324	1,339	46,361	2,318
3.	0,030	1,324	1,339	46,485	2,324
Pomiar 2
1.	0,030	1,15	1,165	43,425	2,171	2,171	9,758
2.	0,030	1,15	1,165	43,416	2,171
3.	0,030	1,15	1,165	43,437	2,172
Pomiar 3
1.	0,030	1,02	1,0345	41,151	2,058	2,056	9,666
2.	0,030	1,02	1,035	41,125	2,056
3.	0,030	1,02	1,035	41,091	2,055

Obliczenia do tabeli

Pomiar 1

- okres T (czas 20 okresów podzielony przez 20)

- śr. wartość okresu T

- wartość przyspieszenia ziemskiego g

Pomiar 2

- okres T (czas 20 okresów podzielony przez 20)

- śr. wartość okresu T

- wartość przyspieszenia ziemskiego g

Pomiar 3

- okres T (czas 20 okresów podzielony przez 20)

- śr. wartość okresu T

- wartość przyspieszenia ziemskiego g

4. Dyskusja błędów

Pomiar 1:

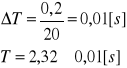
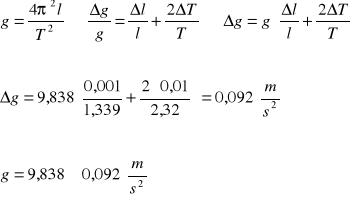
Pomiar 2:

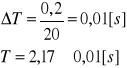
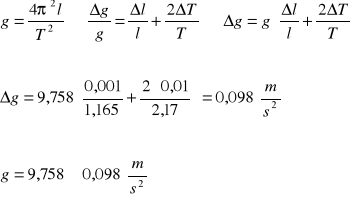
Pomiar 3:

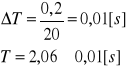
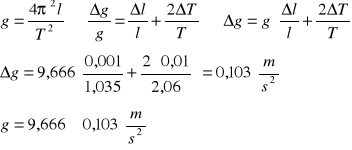
Przy dyskusji błędów jako błąd wynikający z pomiaru 20 okresów przyjęto czas reakcji człowieka tj. 0,2s. Błąd średniej wartości okresu T jest natomiast obliczony jako błąd 20 okresów podzielony przez 20 czyli 0,1s. Należy także uwzględnić iż niedokładny pomiar może wynikać z błędnego odczytu z taśmy mierniczej, zbyt duży kąt wychylenia kulki, błąd obarczony reakcją mierzącego stoperem, błąd wynikający z pomiaru kulki za pomocą suwmiarki. Wszystkie te niedokładności mogą się przyczynić od niedokładnego pomiaru przyspieszenia ziemskiego g.

1 | Strona

---