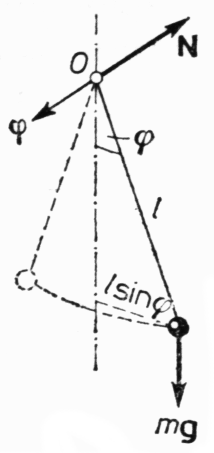
Fizycy przez wahadło rozumieją ciało stałe, które pod wpływem dzia­łania siły ciężkości wykonuje drgania względem nieruchomego punktu lub osi. Rozróżnia się wahadło matematyczne i wahadło fizyczne. Wahadłem matematycznym nazywamy idealny układ, składający się z nieważkiej i nierozciągliwej nici oraz zawieszonej na tej nici punktowej masy. Dobrym przybliżeniem wahadła matematycznego jest niewielka, ciężka kulka, zawieszona na długiej, cienkiej nici.

Wychylenie wahadła z położenia równowagi będziemy opisywać za pomocą kąta ϕ, jaki nić tworzy z pionem (rys). Jeżeli wahadło jest odchylone od pionu, to pojawia się moment N = mglsinϕ (m jest masą, a / — długością wahadła). Moment ten dąży do zawrócenia wahadła z powrotem do położenia równowagi, co jest analogiczne do przypadku działania siły kwazisprężystej. Dlatego wielkościom N i ϕ należy przypisać przeciwne znaki (jeżeli kąt ϕ rozpatrujemy jako wektor ϕ (zgodnie z regułą śruby prawoskrętnej), co jest dopuszczalne dla małych ϕ, to bez trudu zauważamy, że wektory N i ϕ mają przeciwne zwroty). Mamy zatem :

Napiszmy równanie ruchu dla naszego przypadku. Przyspieszenie kątowe oznaczamy symbolem
(druga pochodna ϕ po czasie). Moment bezwładności wahadła wynosi ml² otrzymujemy więc równanie :

Równanie to można sprowadzić do postaci :

Ograniczymy się do analizy małych drgań. W takim przypadku można przyjąć, że sinϕ = ϕ. Oprócz tego wprowadzamy oznaczenie :

Otrzymujemy następujące równanie :

Rozwiązanie ma postać :

Widzimy, że w przypadku małych drgań wychylenie kątowe wahadła matematycznego zależy harmonicznie od czasu.

Ze wzoru na ω_o wynika, że częstość drgań wahadła matematycznego zależy tylko od długości wahadła i przyspieszenia ziemskiego, a nie zależy od masy wahadła. W ten sposób otrzymujemy, otrzymuje się znany wzór na okres drgań wahadła matematycznego:

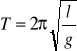
Zauważmy, że równanie można rozwiązać dokładniej. Oto wzór na okres drgań wahadła :

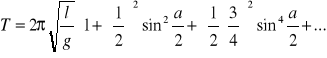
gdzie a jest kątową amplitudą drgań, czyli największym kątem wychylenia wahadła z położenia równowagi.

Jeżeli drgające ciało nie może być uważane za punkt materialny, to wahadło nazywamy wahadłem fizycznym. W wyniku odchylenia wahadła z położenia równowagi o kąt ϕ powstaje moment obrotowy, który stara się zawrócić ciało do położenia równowagi :

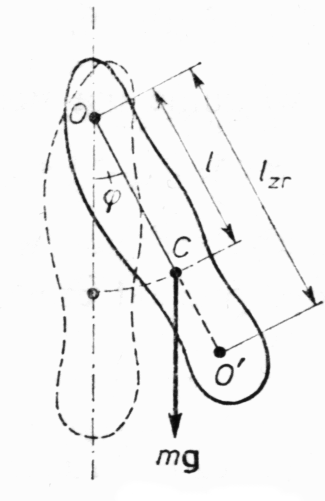
[m jest masą wahadła, a l — odległością punktu zaczepienia O od środka masy C wahadła (rys.)]. Znak " - " ma to samo znaczenie, co w przy­padku wzoru dla wahadła matematycznego.

Moment bezwładności wahadła względem osi przechodzącej przez punkt zawieszenia oznaczamy symbolem I. Możemy napisać, że :

W przypadku małych drgań w/w wzór przechodzi w znane nam już równanie :

Symbol
oznacza tu wielkość :

Z dwóch w/w równań wynika, że w przypadku małych wychyleń z położenia równowagi wahadło fizyczne wykonuje drgania harmoniczne, których częstość zależy od masy, momentu bezwładności względem osi obrotu oraz odległości środka masy wahadła od osi obrotu. Na podstawie powyższego równania okres drgań wahadła fizycznego wynosi :

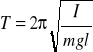
Z porównania wzorów na okres dla wahadeł matematycznego i fizycznego wynika, że wahadło matematyczne o długości :

ma ten sam okres drgań, co dane wahadło fizyczne. Wielkość ta nazywamy długością zredukowaną wahadła fizycznego. Długość zreduko­wana jest więc długością takiego wahadła matematycznego, którego okres drgań jest taki sam, jak okres drgań danego wahadła fizycznego.

Punkt na prostej łączącej punkt zawieszenia ze środkiem masy, odległy o l_zr od osi obrotu, nazywamy środkiem wahań wahadła fizycznego (punkt O' na rys.). Można udowodnić, że w przypadku zawieszenia wahadła w punkcie O' długość zredukowana — a więc i okres — są takie same, jak pierwotnie. Punkt zawieszenia i środek wahań są w tym sensie wzajemnie równoważne: przeniesienie punktu zawieszenia do środka wahań powoduje, że pierwotny punkt zawieszenia staje się nowym środkiem wahań.

Na tej własności oparta jest doświadczalna metoda wyznaczania przy­spieszenia ziemskiego za pomocą tzw. wahadła rewersyjnego Patera. Wa­hadło to ma dwa równoległe do siebie, umocowane w pobliżu końców pryzmaty oporowe, za które można kolejno zawieszać wahadło. Wzdłuż wahadła można przesuwać masywne obciążniki. Taki układ pozwala, by — zawieszone za pomocą każdego z pryzmatów — wahadło miało taki sam okres drgań. W takim razie odległość między oporowymi krawędziami pryzmatów jest równa l_zr . Mierząc okres wahań i l_zr na podstawie wzoru :

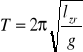
obliczamy wartość przyspieszenia swobodnego spadania g.

---