Poniedziałek 800
Wydział Górniczy |
Imię i nazwisko: 1. Lucyna Szostok 2. Angelika Trawińska |
Rok:
II |
Grupa:
IV |
Nr zespołu:
4 |
|||
Pracowania fizyczna I |
Temat: MODUŁ SZTYWNOŚCI.
|
Nr ćwiczenia: 12 |
|||||
Data wykonania: 15.XI.1999. |
Data oddania:
22.XI.1999. |
Zwrot do poprawy: |
Data oddania: |
Data zal.: |
Ocena: |
||
1.Cel ćwiczenia.
Celem ćwiczenia było wyznaczenie modułu sztywności metodą dynamiczną za pomocą pomiaru okresu drgań skrętnych wibratora.
2. Wprowadzenie teoretyczne.
Moduł sztywności G, jest to stosunek naprężenia stycznego τ do wywoływanego przez nie odkształcenia postaci γ. Wyraża się wzorem:
.
Aby wyznaczyć moduł sztywności wykorzystamy zjawisko skręcenia pręta, którego podatność na skręcenia zależy wyłącznie od szukanego G i wymiarów geometrycznych.
Skręcenie jest odkształceniem spowodowanym przez parę sił przyłożoną do płaszczyzny przekroju poprzecznego pręta o promieniu r i długości l. Podczas skręcania przekroje poprzeczne obracają się wokół osi pręta, a on sam nie zmienia przy tym ani swojej długości l, ani promienia r.
Całkowity moment siły można obliczyć poprzez całkowanie przyczynków pochodzących od pierścieni o promieniu r i grubości dx. Odkształcenie postaci materiału wynosi:
Wartości naprężeń, zgodnie z prawem Hooke'a wynoszą natomiast:
Siła, działająca na pierścień jest dana wzorem:
przez co pierścień daje przyczynek do momentu równy:
Całkowity moment działający na pręt wynosi zatem:
Aby wyznaczyć teraz G, można zastosować metodę statyczną. Wygodniejszym sposobem jest natomiast metoda dynamiczna i z niej właśnie skorzystamy w ćwiczeniu.
Polega ona na pomiarze okresu drgań skrętnych wibratora w postaci pręta, obciążonego ciałem o momencie bezwładności I0. Metoda ta pozwala wyeliminować trudny do wykonania pomiar sił, czy kąta skręcenia.
Pomiar momentu bezwładności Ix wahadła, możemy ominąć poprzez pomiary okresów drgań wahadła samego lub obciążonego ciałem geometrycznie prostym, mającym łatwy do policzenia moment bezwładności I0.
Odpowiednie okresy wynoszą tu: ;
gdzie D jest stałą skręcenia i wynosi:
Moduł sztywności możemy wyznaczyć teraz ze wzoru:
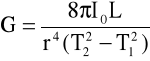
3.Wyniki pomiarów i obliczeń:
Badanym prętem był pręt wykonany ze stali.
Pomiary średnicy:
Lp. |
Średnica pręta stalowego 2r [mm] |
Średnica pręta stalowego 2r [m] |
1 |
2 |
0,002 |
2 |
2 |
0,002 |
3 |
2 |
0,002 |
4 |
1,95 |
0,00195 |
5 |
2 |
0,002 |
6 |
2 |
0,002 |
7 |
1,95 |
0,00195 |
8 |
1,95 |
0,00195 |
9 |
2 |
0,002 |
10 |
2,05 |
0,00205 |
Wartość średnią policzona z wzoru :
![]()
wynosi:
2rśr= 0,000995 [m]
Wszystkie pomiary obarczone są błędem co najmniej Δ2r=0,00001 [m.].
Zmierzona długość pręta wyniosła:
l = 0,71 [m.].
Pomiar długości obarczony jest błędem Δl=0,001 [m].
Wymiary i masy brył obciążających:
- pierścień:
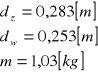
- odważniki (4 szt.):
m=0,139 [kg],
odległość środków odważników od osi obrotu:
a =0,075m.,
pomiar średnic obarczony jest błędem Δd=0,001 [m],
pomiar masy obarczony jest błędem Δm=0,001 [kg].
Dla niewielkiego kąta wychylenia wibratora z położenia równowagi zmierzyłyśmy czas 15 pełnych drgań.
Pomiary drgań wibratora:
Lp. |
Czas drgania wibratora nie obciążonego t1 [s] |
Okres drgań T1 [s] |
Czas drgania wibratora obciążonego pierścieniem t2p [s] |
Okres drgań T2p [s] |
Czas drgania wibratora obciążonego krążkami t2k [s] |
Okres drgań T2k [s] |
1 |
32,64 |
2,17 |
44,97 |
2,99 |
35,03 |
2,33 |
2 |
32,88 |
2,19 |
44,98 |
2,99 |
34,73 |
2,32 |
3 |
32,56 |
2,17 |
44,55 |
2,97 |
34,75 |
2,31 |
4 |
32,12 |
2,14 |
44,75 |
2,98 |
34,94 |
2,33 |
5 |
32,72 |
2,18 |
44,99 |
2,99 |
34,82 |
2,32 |
6 |
32,25 |
2,15 |
44,84 |
2,98 |
35,01 |
2,33 |
Wartości średnie okresów dla poszczególnych pomiarów zostały policzone z następującego wzoru:
![]()
Błąd standardowy liczymy z wzoru:
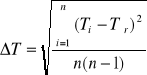
Błąd względny wartości okresu obliczony ze wzoru:
![]()
Tabela z policzonymi błędami:
Rodzaj błędu |
Okres drgań T1 [s] |
Okres drgań T2p [s] |
Okres drgań T2k [s] |
Wartości średnie okresów Tśr [s] |
2,15 |
2,99 |
2,33 |
Błąd standardowy ΔT [s] |
0,0078 |
0,0047 |
0,0035 |
Błąd względny δ [%] |
0,36 |
0,16 |
0,15 |
Obliczenie wartości momentu bezwładności I0 na podstawie zmierzonych wartości masy i wymiarów geometrycznych:
- dla pierścienia:
dw=0,253 [m],
dz=0,283 [m],
m=1,03 [kg],
![]()
- dla krążka wzór powyższy się upraszcza.
m=0,139 [kg],
odległość środków odważników od osi obrotu a =0,075m.,
Obliczone momenty bezwładności:
obręcz
Io=0,01855 [kg.m2],
- układ krążków
Io=0,00313 [kg.m2].
![]()
Oszacowanie błędów pomiarów Io dokonano na podstawie prawa przenoszenia błędów:
gdzie:
Δd=0,001 [m],
Δm=0,001 [kg].
Błąd ten wynosi:
ΔI0=0,56.10-3 [kg.m2].
Obliczanie modułu sztywności.
Moduł sztywności obliczamy ze wzoru:
![]()
gdzie:
l - długość pręta [m.],
I0 - moment bezwładności [kg.m2],
r - promień pręta [m],
T - wartości średnie okresów dla poszczególnych pomiarów.
dla pręta stalowego otrzymujemy:
dla obręczy:
G= 79,69 [GPa];
- dla odważników:
G= 80,77 [GPa];
Wartość średnia:
GSr= 80,23 [GPa];
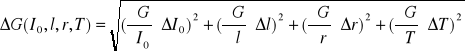
Oszacowanie błędów pomiarów dokonano na podstawie prawa przenoszenia błędów:
gdzie:
Δl=0,001 [m],
Δr=0,001 [m],
ΔTśr= 0,0053 [s],
ΔI0=0,56.10-3 [kg.m2] (dla pierścienia jest większy więc ten jest brany pod uwagę).
po zróżniczkowaniu i wstawieniu wartości liczbowych otrzymujemy:
![]()
=![]()
![]()
=![]()
![]()
=![]()
![]()
=![]()
Sumaryczny błąd pomiaru:
ΔG =![]()
Błąd względny wartości modułu sztywności obliczony ze wzoru:
![]()
wynosi on:
δ=3,8 [%].
4 Wnioski.
Tablicowa wartość modułu sztywności dla stali pospolitej wynosi G=78-82 [GPa]. Obliczona wartość modułu sztywności mieści się w zakresie podanym dla wartości tabelarycznej. Wartość oszacowanego błędu okresów T nie przekracza 1 [%] i jest dokładną wartością. Natomiast błąd z jakim został wyznaczony moduł sztywności G jest rzędu 4 [%]. Jest to wartość niezadowalająca. Największy wpływ na ten błąd miały przyczynki od wyznaczenia momentu bezwładności (z tym się wiążą błędy podczas wyznaczania masy i wymiarów geometrycznych obciążników) oraz od pomiaru promienia pręta. Otrzymane wartości modułu sztywności G dla wibratora obciążonego pierścieniem i krążkami różniły się zaledwie 1,08 [GPa] i obydwie mieszczą się w zakresie wartości tabelarycznej.
![]()
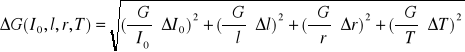
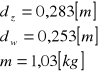
Wyszukiwarka
Podobne podstrony:
labolatorium2, agh wimir, fizyka, Fizyka(1)
10 moj konspekt, agh wimir, fizyka, Fizyka(1)
konspekt(1), agh wimir, fizyka, Fizyka(1)
samoindukcja cewki, agh wimir, fizyka, Fizyka(1)
Kospekt teoria, agh wimir, fizyka, Fizyka(1)
labolatorium4, agh wimir, fizyka, Fizyka(1)
tabele9, agh wimir, fizyka, Fizyka(1)
22wstep, agh wimir, fizyka, Fizyka(1)
Opracowanie 10, agh wimir, fizyka, Fizyka(1)
fizyka 2, agh wimir, fizyka, Fizyka
22opr, agh wimir, fizyka, Fizyka(1)
ZESTAW2A, agh wimir, fizyka, fiza
7 konspekt, agh wimir, fizyka, Fizyka(1)
konspekt Cw5, agh wimir, fizyka, Fizyka(1)
lab22wyniki, agh wimir, fizyka, Fizyka(1)
Mikrofale do druku, agh wimir, fizyka, Fizyka(1)
więcej podobnych podstron