„Podstawy termodynamiki”, grupa 2 - semestr 3, konspekto-ściąga , 9 stycznia 2008 plik 2R-TermTabPodstPrzew1
[ wg „ Krzepnięcie i zasilanie odlewów” - Lab. nr 2 ] 18.10.2007wer.22:
KRÓTKI PRZEGLĄD PODSTAWOWYCH ZAGADNIEŃ ZWIĄZANYCH Z PROCESEM PRZEWODZENIA CIEPŁA
Wprowadzenie i podstawowe pojęcia
` Warunkiem zrozumienia podstawowych zagadnień wymiany ciepła na drodze przewodzenia jest dokładna znajomość podstawowych pojęć niezbędnych do matematyczno-fizycznego opisu przebiegu tego procesu. Wymienimy tu przykładowo pojęcia:
układ podlegający badaniu,
ustalone (stacjonarne) i niestacjonarne (nieustalone) pole temperatury,
liniowe, płaskie i przestrzenne pole temperatury,
gradient temperatury,
pojęcie i równanie opisujące gęstość strumienia cieplnego,
podstawowe i „rozszerzone” parametry termofizyczne badanych ciał ( 5 parametrów),
opory cieplne przewodzenia i wymiany ciepła,
warunki jednoznaczności jako podstawa strategii rozwiązywania ogólnego równania różniczkowego przewodzenia ciepła (Fouriera).
Układem nazywamy wydzielony obszar przestrzenny w którym zachodzą wszystkie procesy podlegające badaniom, analizie i ujęciu w postaci bilansu ciepła, masy i energii. Nieustalone pole temperatury ( nie temperatur !) to zależność funkcyjna w której zmienną zależną jest wartość temperatury a zmiennymi niezależnymi współrzędne położenia i czas. Jeżeli pole jest stacjonarne (ustalone) to zależy wyłącznie od współrzednych, czyli nie zależy od czasu. Można też powiedzieć, że stacjonarny oznacza: niezmienny w czasie.
Zależnie od liczby współrzędnych pole temperatury może być:
liniowe, T= f( x,
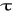
) lub T= f(x),płaskie, T= f( x, y,
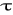
) lub T= f( x, y),przestrzenne, T= f( x, y, z,
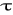
) lub T= f( x, y,z).
Przypadki pola płaskiego i przestrzennego są bardzo trudne a czasem niemożliwe do matematycznego opisu, wymagającego całkowania równania różniczkowego przewodzenia ciepła. Dlatego uproszczone modele matematyczne dotyczą bardzo często przypadku liniowego pola temperatury.
Gęstość strumienia cieplnego „q” jest to ilość ciepła wymieniana przez jednostkową powierzchnię ciała odniesiona do jednostki czasu, czyli:
![]()
[ ![]()
] (1)
gdzie: F - pole powierzchni [ m 2] przez którą przepływa elementarne ciepło dQ,
dQ - elementarne ciepło [ J ],
![]()
- czas [ s ].
Pojęcie gradientu temperatury definiowane jest ogólnie za pomocą pochodnej :
gradT = ![]()
(2a)
a dla ustalonego, liniowego pola temperatury { T= f(x) } w postaci:
gradT = ![]()
(2b)
Podstawowymi parametrami ( współczynnikami) termofizycznymi (materiału formy, odlewu, materiałów izolacyjnych itp.) decydującymi o przebiegu procesu przewodzenia ciepła są:
a) ![]()
- współczynnik przewodzenia ciepła 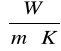
, (![]()
to litera „lambda”),
b) c - ciepło właściwe 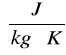
,
c) ![]()
- gęstość masy lub krótko gęstość ![]()
, ( litery „ro” nie należy mylić z literą”p”).
Dla ułatwienia matematycznego ujęcia przebiegu procesów cieplnych wprowadzono ponadto tzw. „rozszerzone” parametry termofizyczne ( materiału formy, odlewu itp.), definiowane w oparciu o parametry podstawowe.
Należą do nich: współczynnik wyrównywania temperatury „a” (inna nazwa to współczynnik przewodzenia temperatury) i współczynnik akumulacji ciepła „b”.
Współczynnik wyrównywania temperatury definiowany jest wzorem:
![]()

Natomiast współczynnik akumulacji ciepła określony jest zależnością:
![]()
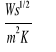
Nazwa tego współczynnika wynikła z faktu, że w pewnych zagadnieniach przewodzenia ilość akumulowanego w ciele ciepła jest proporcjonalna do wartości współczynnika akumulacji ciepła.
Niezbędnym warunkiem rozwiązania podstawowego równania rożniczkowego przewodzenia ciepła (Fouriera) odzwierciedlającego konkretny przypadek wymiany ciepła jest sformułowanie tzw. warunków jednoznaczności, czyli dodatkowych warunków ściśle określających rozpatrywane zagadnienie. Pozwala to na wydzielenie z nieskończonej liczby zjawisk przewodzenia ciepła - spełniających równanie różniczkowe Fouriera - ściśle określonego procesu, będącego przedmiotem naszych badań i uzyskanie jego matematycznego opisu, najczęściej w postaci równania pola temperatury.
W skład warunków jednoznaczności wchodzą:
1. warunki geometryczne, określające kształt badanego układu lub części w której zachodzi badany proces cieplny,
2. warunki fizyczne, opisujące właściwości ( parametry) termofizyczne wszystkich podobszarów układu ( np. metalu odlewu, materiału formy, materiału izolacyjnego),
3. warunki początkowe, określające pole temperatury układu w momencie przyjętym jako początkowy (![]()
= 0 ), przy czym występują one tylko w procesach nieustalonego przepływu ciepła, w których występuje nieustalone pole temperatury.
4. warunki brzegowe, które mogą być zadawane 4. sposobami.
Warunki brzegowe 1. i 3. rodzaju (najczęściej stosowane i oznaczane symbolami WB1r i WB3r) zostaną opisane w punkcie 3.
Ustalony przepływ ciepła przez ściankę płaską, opory cieplne
Równanie różniczkowe opisujące ustalone, liniowe temperatury ma postać:
![]()
(1)
Wynika stąd wartość gradientu temperatury:
gradT = ![]()
(2)
gdzie:
T1pow,T2pow - temperatury obu powierzchni ścianki płaskiej,
.g - grubość ścianki ( oznaczana często przez „ d ” ).
Zgodnie z prawem Fouriera
.q = - λ gradT otrzymujemy dla ścianki płaskiej
![]()
(3)
.lub
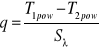
(4)
Postać równania (4) uzyskano przy założeniu znajomości warunków brzegowych 1. Rodzaju (WB1r). Parametr cieplny występujący w mianowniku równania (4) nazywany jest oporem przewodzenia ciepła:
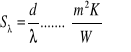
(5)
W odniesieniu do warunków brzegowych 3. rodzaju (WB3r) wprowadzono tzw. opór wymiany ciepła, równy:
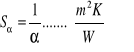
(6)
W przypadku ścianki wielowarstwowej (WB1r) w mianowniku równania (4) wystąpi suma wszystkich oporów cieplnych Sλ.
W przypadku przepływu ciepła - rozpatrywanego z wykorzystaniem WB3r -
w mianowniku równania (4) wystąpi suma wszystkich oporów cieplnych ( S α , S λ ).
Nieustalone pole temperatury półprzestrzeni (nagrzewanie lub stygnięcie)
Jeżeli badany układ (np. odlew-forma) spełnia warunki teoretycznego modelu jednokierunkowego przepływu ciepła na drodze przewodzenia, to jest uzasadnione matematyczne ujęcie procesu w postaci równania różniczkowego przewodzenia ciepła Fouriera:
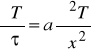
( 2)
. gdzie:
T - temperatura [K]
x - współrzędna (odległość) [m]
![]()
- czas [s]
a - współczynnik wyrównywania temperatury
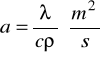
( 3)
Jak już wspomniano wyżej, warunkiem rozwiązania równania Fouriera (1) jest sformułowanie warunków jednoznaczności. Poniżej wyjaśnimy sens matematyczno-fizyczny warunków brzegowych.
Warunki brzegowe
Warunki brzegowe 1. go rodzaju (WB1r) polegają na ujęciu rozkładu temperatury na powierzchni kontrolnej układu ( tzw. temperatura powierzchni) w rozpatrywanym zakresie czasowym, czyli na zadaniu funkcji ogólnego typu
![]()
Przypadkiem szczególnym i najczęściej stosowanym są tzw. ustalone warunki brzegowe
( niezmienność temperatury powierzchni) co można zapisać w postaci:
![]()
co oznacza niezmienność temperatury na powierzchni układu ( indeks „pow”) w czasie trwania procesu wymiany ciepła ( [1] - s. 30).
Warunki brzegowe 3. go rodzaju (WB3r) polegają na zadaniu temperatury otoczenia układu oraz na zadaniu prawa wymiany ciepła z otoczeniem. W najczęściej stosowanym przypadku kinetykę procesu cieplnego ujmuje tzw. współczynnik wymiany ciepła użyty przez Newtona w równaniach opisujących gęstość strumienia cieplnego. Rozróżnia się tu dwa przypadki :
- dla procesu stygnięcia układu
![]()
, ( 4a)
- dla procesu nagrzewania
![]()
(4b)
gdzie:
![]()
- współczynnik wymiany ciepła ![]()
![]()
- temperatura otoczenia.
Warunki brzegowe drugiego rodzaju polegają na odpowiednim określeniu strumienia cieplnego i stosowane są bardzo rzadko. Natomiast warunki brzegowe 4. rodzaju są bardzo przydatne w ujęciu procesu krzepnięcia metodą symulacji numerycznej.
5. Nagrzewanie półprzestrzeni przy ustalonych warunkach brzegowych 1. rodzaju.
Warunkiem wyznaczenia gęstości strumienia cieplnego jest znajomość nieustalonego pola temperatury badanego ciała czyli półprzestrzeni. Stwarza to też możliwość ilościowego ujęcie wartości akumulowanego ciepła, co jest podstawą do zapisu ewentualnego bilansu przepływu ciepła w układzie.
T
Tpow = const
q
Tx
T0
x x
Xp
Rys.1. Schemat pola temperatury półprzestrzeni dla dwu momentów czasowych ( τ1, τ2 )
Układ ( rys. 1) ograniczony nieskończenie dużą powierzchnią płaską (płaszczyzną) i rozbudowany od tej powierzchni w nieskończoność nazywamy półprzestrzenią. Wielkość Xp jest umowną głębokością przegrzania półprzestrzeni. Parametry występujące na rys. 1 zostaną opisane poniżej.
Każdy proces nagrzewania i stygnięcia ciała jest procesem cieplnym nieustalonym, czyli przebiega przy nieustalonym polu temperatury. Podstawą do określenia funkcji opisującej pole temperatury półprzestrzeni jest ogólne równanie różniczkowe przewodzenia ciepła (1). Warunki konieczne do jego całkowania nazywa się warunkami jednoznaczności.
Warunki jednoznaczności:
fizyczne - określają parametry
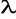
,c,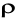
, w tym przypadku jako niezmienne w czasie procesu nagrzewania,geometryczne - ciało ma kształt półprzestrzeni,
początkowe - temperatura półprzestrzeni w momencie przyjętym jako początek procesu jest stała w całej masie , czyli To jest tzw. temperaturą początkową dla czasu „
zerowego” czyli:
dla ![]()
![]()
brzegowe - 1.go rodzaju (WB1r).
Rozwiązaniem równania ( 1 ) jest funkcja opisująca pole temperatury półprzestrzeni, zwana ( co wynika z postaci matematycznej) funkcją błędów Gaussa ( er f = error function):
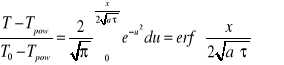
( 5 )
![]()
Podstawową wielkością fizyczną wynikającą z równania (5) jest gęstość strumienia cieplnego, przy czym do bilansu cieplnego istotna jest jej wartość na powierzchni kontrolnej. Po wyznaczeniu gradientu (pochodnej) i zastosowaniu prawa Fouriera
![]()
otrzymamy dla powierzchni ( x = 0) bardzo ważny wzór na wartość strumienia cieplnego :
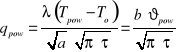
( 6)
![]()
- współczynnik akumulacji (7)
![]()
- (małe theta) spiętrzenie (różnica) temperatury [K] , (różnica rozpatrywanej temperatury i początkowej, „minimalnej” temperatury układu)
![]()
- bezwymiarowa temperatura , definiowana dla WB1r ( inaczej dla WB3r !) wzorem:
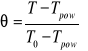
(8)
Dla obliczenia całkowitego ciepła wymienianego przez powierzchnię półprzestrzeni (ciepło akumulowane, wydatek ciepła) korzysta się z równania bazowego wiążącego ciepło ogólne, strumień cieplny, powierzchnię i czas. Można to zapisać:
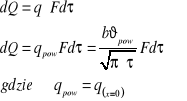
Całkowite ciepło stygnięcia lub nagrzewania uzyskuje się po całkowaniu i wyrażone jest :
![]()
(9)
Równanie (9) wyraża niezbędny składnik bilansu cieplnego dla odlewu krzepnącego w formie piaskowej spełniającej warunek półprzestrzeni w sensie cieplnym.
Przykładowe pytania kolokwialne
Opisać pojęcia : układu, niestacjonarnego (nieustalonego) pola temperatury, gradientu temperatury, gęstości strumienia cieplnego, podstawowych parametrów termofizycznych.
Określić pojęcie warunków geometrycznych, fizycznych i brzegowych.
Rodzaje i definicje oporów cieplnych
Gęstość strumienia cieplnego dla ustalonego przepływu przez ściankę płaską dwuwarstwową dla WB1r.
Gęstość strumienia cieplnego dla ustalonego przepływu przez ściankę płaską dla WB3r.
Prawo Fouriera.
Pojęcie warunków jednoznaczności (1, 2, 3, 4).
Zdefiniować pojęcia i podać jednostki: gradT, λ, .a , b , To,
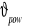
(2, 3, 4).Podaj 3 podstawowe i 2 uzupełniające parametry termofizyczne ciał stałych oraz ich jednostki.
Wymienić parametry opisujące proces nagrzewania półprzestrzeni przy WB1r.
Nieustalone pole temperatury półprzestrzeni przy ustalonych warunkach WB1r.
Definicja i wykres funkcji błędów Gaussa.
Literatura
1. W. Longa: Krzepnięcie odlewów. Wyd. Śląsk 1985 ( strony: : 195, 16, 29, 74 ....)
2. W. Longa i in. : Stygnięcie i krzepnięcie odlewów - laboratorium. Skrypt AGH
nr 623. Kraków 1978 .
3. Wykłady w semestrze zimowym 2007/2008.
4. Instrukcje do laboratorium z przedmiotu „ Krzepniecie i zasilanie odlewów ”.
Opracował dr inż. Adam Gradowski
1.0
0.8
0.6
0.4
0.2
0.0
0.0 0.6 1.2 1.8 2.4 3.0
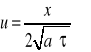
Wyszukiwarka
Podobne podstrony:
2R TermLabor OCE LISTA # W17 # G1G2G3 (Metal.) G4 (Wirtot.) 2012-13 #Akt17#, Studia
roln agrochemia 2r-1, Szkoła Rolnictwo studia, Szkoła, Materiały studia, chemia rolna
2R-Lab-2011nx-Harmon-wx4-1, Studia
2R-Instrukcja1-Profil-wer 31PP, Studia
Studia slajdy1
Studia slaidy
oszustwa studia cywilne
Mazowieckie Studia Humanistyczn Nieznany (11)
Mazowieckie Studia Humanistyczne r2001 t7 n2 s157 160
Mazowieckie Studia Humanistyczne r1996 t2 n1 s165 173
Mazowieckie Studia Humanistyczne r1998 t4 n1 s79 101
Mazowieckie Studia Humanistyczn Nieznany (14)
Mazowieckie Studia Humanistyczne r1997 t3 n1 s290 292
Mazowieckie Studia Humanistyczne r1996 t2 n1 s113 126
Mazowieckie Studia Humanistyczne r2002 t8 n2 s109 114
eis 2002 10 adaptacja akustyczna domowego studia
Krwawienie, studia pielęgniarstwo
fotosynteza i metabolizm-ściąga, Pomoce naukowe, studia, biologia
więcej podobnych podstron