Fizyka I - egzamin.

Opracowanie pytań.

1.Wektor - definicja, właściwości, przykłady:

Definicja: Wektorem nazywamy uporządkowaną parę punktów, z których jeden jest początkiem, a drugi końcem wektora. Odległość między tymi punktami nazywamy długością wektora (modułem). Wektor to dowolna wielkość fizyczna opisana przez trzy liczby, które przekształcają się przy zmianie układu współrzędnych. Wektor, którego początkiem i końcem jest ten sam punkt nazywamy wektorem zerowym.

Właściwości:

1. Kierunek- prosta, na której działa dana wielkość

2. Zwrot- strona, w którą zwrócony jest wektor, graficznie określona symbolem strzałki

3. Wartość- reprezentowana przez długość wektora

4. Punkt zaczepienia

Przykłady:

1.Wektor przemieszczenia- ma wartość bezwzględną oraz kierunek

2. Wektor siły- określający wartość kierunek przykładowej siły przyłożonej do układu

2.Tensor- definicja, właściwości, przykłady:

Definicja: tensor jest to uogólnienie pojęcia wektora, wielkości której własności pozostają identyczne, niezależnie od wybranego układu współrzędnych.

Właściwości:

1.Wektor jest tensorem pierwszego rzędu.

2. Tensor drugiego rzędu jest reprezentowany macierzowo. Ustala zależności między wektorami.

Przykłady:

1. Związek między wektorem indukcji elektrycznej: D i wektorem natężenia pola elektrycznego: E

| Dx | | εxx εxy εxz | |Ex|

| Dy | = εo | εyx εyy εyz | |Ey|

| Dz | | εzx εzy εzz | |Ez|

2. Inne przykłady: naprężenia, odkształcenia

3. Tensor trzeciego rzędu: tensor modułów piezoelektrycznych d(ijk):

γ(jk)= d(ijk) E(i)

|

Tensor (drugiego rzędu) odkształceń

3. Iloczyn skalarny- definicja, właściwości, przykład:

Definicja: Iloczynem skalarnym dwóch wektorów np. oznaczonych za pomocą ā i ē, zapisywanym jako ā · ē jest skalar o wartości: ā · ē= ae cosφ , przy czym φ jest kątem utworzonym przez kierunki wektorów ā i ē, a- modułem wektora ā, e- modułem wektora ē

Właściwości:

1. Iloczyn skalarny może być liczbą dodatnią, ujemną lub 0, w zależności od wartości kąta γ

2. Przemienność: ā · ē= ē· ā

3. Prostopadłość dwóch niezerowych wektorów: ā ┴ ē ↔ ā · ē= 0

Zastosowanie:

1. Prawo cosinusów: jeśli C= A+B to: C^2= A^2 + B^2 + 2AB cos<(A,B)

2. Cosinusy kierunkowe: A= x(A·x)+ y(A·y)+ z(A·z)

Przykład:

Moc(P) jako prędkość(v) wykonywanej pracy(W) przy stałej sile(F):

P=dW/dt= d(F·r)/dt= F·(dr/dt)= F·v

4. Iloczyn wektorowy- definicja, właściwości, przykład:

Definicja: Iloczynem wektorowym dwóch wektorów ā i ē oznaczanym jako ā × ē jest wektor c o długości : c=ae sinφ. Przy czym φ jest mniejszym z kątów pomiędzy wektorami ā i ē.

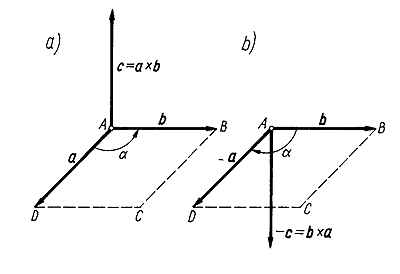
Jego zwrot wyznaczamy przy pomocy reguły śruby prawoskrętnej

Właściwości:

1. Antyprzemienność- iloczyn wektorowy nie jest przemienny: A×B= -B×A

2. Jeśli wektory są równoległe to iloczyn wektorowy równa się zeru: A׀׀ B -> A×B= 0

( bo sinus 180˚=0)

Przykłady: Moment pędu punktu materialnego (L) jest iloczynem wektorowym wektora łączącego punkt, względem którego określa się moment pędu i punktu ciała (r) oraz wektora pędu punktu materialnego (p): L = r × p

5. Układy współrzędnych ( kartezjański, biegunowy, sferyczny, walcowy) - opis:

1.Układ współrzędnych: funkcja przypisująca każdemu punktowi danej przestrzeni skończony ciąg liczb rzeczywistych zwanych współrzędnymi punktu.

2.Kartezjański układ współrzędnych: zwany również prostokątnym układem współrzędnych, w którym dane są: punkt zwany środkiem lub początkiem układu, którego wszystkie współrzędne równe są 0; zestaw n osi liczbowych zwanych osiami układu współrzędnych, z których każde dwie są do siebie prostopadłe i których zera znajdują się w wybranym początku układu

6. Klasyfikacja ruchów w kinematyce:

Kinematyka- zajmuje się związkami pomiędzy położeniem, prędkością i przyspieszeniem badanej cząstki.

1. Ze względu na tor (trajektorię) ruchu:

- prostoliniowe (postępowe)

- krzywoliniowe (w tym : po okręgu, rzuty ukośne)

2. Ze względu na zależność położenia od czasu:

- jednostajne

- jednostajnie zmienne : przyspieszone [jednostajne przyspieszenie oznacza stałość przyspieszenia od czasu. r(t)= ro +vot+(at^2)/2 v(t)=vo+at a(t)=const(t) ], opóźnione [ a skierowany przeciwnie do vo, prędkość jest liniową funkcją czasu i maleje wraz z jego upływem, a przyspieszenie jest stałe r(t)= ro +vot - (at^2)/2 v(t)=vo - at ]

- pozostałe

3. Ruch jednostajny prostoliniowy: („jednostajność” oznacza liniową zależność położenia od czasu i stałość prędkości: r(t)= ro+ vot v(t)≡vo=const(t)

ro≡r(0)- to wektor położenia początkowego (związany z wyborem układu współrzędnych)

vo≡v(0)- to wektor prędkości początkowej (w tym wypadku jest ona stała w czasie całego ruchu)

4.Ruch krzywoliniowy: ruch, który odbywa się po torze krzywoliniowym (tor jest linią krzywą), a o jego rodzaju decydują dwie składowe przyspieszenia całkowitego:

- przyspieszenie styczne

|as|=dv/dt charakteryzuje szybkość zmiany liczbowej wartości prędkości ruchu

gdy as=0 to ruch nazywamy jednostajnym

gdy as = const≠0 to jest to ruch jednostajnie zmienny

- przyspieszenie normalne:

|an|=v^2/ R charakteryzuje szybkość zmiany kierunku prędkości ruchu; w ruchu prostoliniowym an=0

Promień krzywizny R definiowany poprzez 1/R=∆α/∆s

- przyspieszenie całkowite: a=an+as a=√an^2+as^2

7.Wielkości kinematyczne (ogólne)- podstawowe definicje

1.Prędkość: wielkość wektorowa, która określa zarówno szybkość ruchu, jak i jego kierunek w danej chwili

Prędkość chwilowa

v≡lim(r(t) - r(to))/(t-to)≡dr/dt

^t->to

Jednostką jest metr na sekundę.

2. Przyspieszenie- wielkość wektorowa, która określa zmiany wektora prędkości w czasie (zarówno wartości, jak i kierunku).

Przyspieszenie chwilowe

a≡lim(v(t)-v(to))/(t-to)≡dv/dt=d^2r/dt^2

^t->to

Jednostka: metr na sekundę na sekundę.

8.Wielkości kinematyczne w ruchu po okręgu - definicje

1.W ruchu po okręgu przyspieszeniem normalnym (an) nazywamy przyspieszenie dośrodkowe (ad). Zawsze spełniony jest warunek, że as┴ad. (as- przyspieszenie styczne)

W tym ruchu as=0 i ad= v^2/R.

2. Kątowe wielkości kinematyczne:

- prędkość kątowa ω≡dα/dt - stosunek zmiany kąta wyrażonego w radianach do czasu w jakim został zatoczony przez ciało. Jednostka [rad/s]. Pseudowektor.

- przyspieszenie kątowe ε≡dω/dt≡d^2ω/dt^2 - stosunek zmiany prędkości kątowej do czasu w jakim ta zmiana nastąpiła

3. Parametry ruchu po okręgu:

- okres ruchu: czas jednego, pełnego obiegu ciała po okręgu. Wyraża się wzorem: T=2π/ω.

- częstotliwość obiegu: f≡1/T=ω/2π

4. Związki pomiędzy wielkościami kątowymi i liniowym w ruchu po okręgu:

v=ω×R a=ε×R

9.Rzut ukośny- definicja, równania ruchu, równanie trajektorii

1. Rzut ukośny to ruch ciała w polu grawitacyjnym (w dwóch wymiarach), który jest złożeniem dwóch ruchów - w kierunku osi „x” oraz w kierunku osi „y”. Zgodnie z zasadą superpozycji (zasada niezależności ruchów- jeśli jakiś punkt bierze jednocześnie udział w kilku ruchach, to wypadkowe przesunięcie punktu równe jest sumie wektorowej przesunięć wykonanych przez ten punkt w tym samym czasie w każdym z tym ruchów oddzielnie) ruch ten można opisać jako dwa niezależne ruchy:

- ruch w kierunku „x” : jednostajny z prędkością vox=vocosα

- ruch w kierunku „y” : jednostajnie opóźniony z prędkością początkową (vo) i przyspieszeniem (g) voy=vosinα

2.Równanie trajektorii (parabola)

- przemieszczenie punktu w poziomie od jej położenia początkowego xo, jest dane wzorem:

x-xo=voxt; ponieważ vox=vocosα, więc : x-xo=(vocosα)t (1)

-przemieszczenie punktu w pionie:

y-yo= voyt- 1/2gt^2= (vosinα)t- 1/2gt^2 (2) (korzystając z ogólnego wzoru na ruch jednostajnie opóźniony, za przyspieszenie przyjmując przyspieszenie ziemskie)

vy=vosinα- gt

- wyznaczając t z równania (1) i podstawiając do równania (2) otrzymujemy:

y=(tgα)x - (gx^2)/(2(vocosα)^2) RÓWNANIE TORU

10.Zasady dynamiki Newtona

1.Dynamika: to dział mechaniki, w którym bada się związki między wzajemnymi oddziaływaniami ciał i zmianami ich ruchu. Dynamika zajmuje się siłami działającymi na ciała i źródłami tych sił.

2.I zasada dynamiki Newtona: (zasada bezwładności) Każde ciało pozostaje w spoczynku lub porusza się ruchem jednostajnym prostoliniowym, dopóki działanie innych ciał nie zmusi go do zmiany tego stanu. Ciała pozostaje w stałym spoczynku lub stałej prędkości, gdy jest pozostawione samo sobie (działająca na nie siła wypadkowa jest równa 0 ).

Fwyp=0 -> a=0

3.II zasada dynamiki Newtona: Korzystając z pojęcia pędu: pędem cząstki jest wektor p zdefiniowany jako p=mv, przy czym m jest masą cząstki a v jego prędkością, możemy zdefiniować II zasadę dynamiki Newtona: szybkość zmiany pędu ciała jest równa sile wypadkowej działającej na to ciało: Fwyp=dp/dt. Dla ciała o stałej masie: dp/dt=d(mv)/dt=m(dv/dt)=ma

Zmiana ruchu jest proporcjonalna do przyłożonej siły i zachodzi w kierunku działającej siły.

a=Fwyp/m

Jeżeli na ciało działa stała, niezrównoważona siła wypadkowa, to ciało to porusza się ruchem jednostajnie przyspieszonym z przyspieszeniem proporcjonalnym do tej siły a odwrotnie proporcjonalnym do masy - miary bezwładności tego ciała.

4.III zasada dynamiki Newtona: Działania na siebie dwóch ciał są zawsze równe, lecz przeciwnie skierowane.

Gdy dwa ciała oddziałują wzajemnie, to siła wywierana przez ciało drugie na pierwsze jest równa i przeciwnie skierowana, do siły jaką ciało pierwsze działa na ciało drugie:

Fa->b= - Fb->a

Te siły oddziaływania między ciałami nazywane są siłami reakcji (lub siłami oddziaływania)

5. Wszystkie zasady dynamiki Newtona spełnione są tylko wtedy gdy rozpatruje się je w inercjalnych układach odniesienia ( czyli w takich, w których każde ciało porusza się ruchem jednostajnie prostoliniowym lub spoczywa gdy nie działa na nie żadna siła - spełniona jest I zasada dynami Newtona)

11. Pęd i zasada zachowania pędu

1.Pędem cząstki jest wektor p zdefiniowany jako : p=mv , przy czym m jest masą cząstki a v jej prędkością. Ponieważ masa jest zawsze dodatnią wielkością skalarną, to wektory p i v mają zawsze ten sam kierunek. Jednostką pędu jest kilogram razy metr na sekundę. Korzystając z pojęcia pędu możemy zdefiniować II zasadę dynamiki Newtona( pytanie wyżej).

2.Pęd układu cząstek: pęd układu cząstek jest równy iloczynowi całkowitej masy układu - mu oraz prędkości jego środka masy: P= mu Vśm.

Zmiana pędu układu jest równa wypadkowej sił zewnętrznych, działających na układ.

3.Zasada zachowania pędu: Jeśli na układ nie działają żadne siły zewnętrzne (tzn. układ jest izolowany) lub ich wypadkowa jest równa zeru oraz żadne cząstki nie opuszczają układu ani do niego nie przybywają (tzn.układ jest zamknięty), to całkowity pęd nie ulega zmianie.

P=const

Całkowity pęd układu w pewnej chwili początkowej tpocz = całkowity pęd układu w dowolnej chwili późniejszej tkońc.

Ppocz= Pkońc

Powyższe równania są równaniami wektorowymi, więc każde z nich jest równoważne trzem równaniom wyrażającym zachowanie pędu wzdłuż trzech wzajemnie prostopadłych kierunków np. osi układu współrzędnych xyz. W zależności jakie siły działają na układ, pęd może nie być zachowany wzdłuż wszystkich trzech kierunków, a tylko wzdłuż jednego lub dwóch. Prawdziwe jest przy tym następujące stwierdzenie: Jeśli wypadkowa sił zewnętrznych działających na układ zamknięty ma wzdłuż pewnej osi składową równą 0, to składowa pędu wzdłuż tej osi nie ulega zmianie.

12.Nieinercjalne układy odniesienia: siła Coriolisa

1.Nieinercjalny układ odniesienia: układ, który porusza się ruchem niejednostajnym względem jakiegokolwiek układu inercjalnego( czyli takiego, w którym spełniona jest I zasada dynamiki Newtona).

Działają w nim siły bezwładności: można je mierzyć ( np. wagą sprężynową), lecz nie sposób związać ich z żadnymi ciałami, od których mogłyby pochodzić, dlatego nie można stosować do nich III zasady dynamiki Newtona).

2. Zjawiska, które można wytłumaczyć, tylko wtedy gdy przestanie zaniedbywać się „odstępstwa od inercjalności” układu:

- obrót płaszczyzny wahań wahań wahadła (wahadło Foucault)

- podmywanie prawych brzegów rzek na półkuli północnej, lewych na półkuli południowej

- odchylanie się na wschód na półkuli północnej ciał swobodnie spadających, analogicznie na zachód na półkuli południowej

3.Siła Coriolisa: jest siłą bezwładności występującą w nieinercjalnym układzie odniesienia, związana jest ona z ruchem postępowym ciał w układzie obracającym się (układ obracający się jednostajnie z prędkością kątową ωo i poruszający się ze stałą prędkością vo). Jest ona skierowana prostopadle do płaszczyzny wyznaczonej przez iloczyn wektorowy wektorów prędkości kątowej ω i prędkości vw- prędkość wypadkowa. Siła ta opisana jest wzorem:

Fc= -2m(ω×vw)

4.Przykłady siły Coriolisa:

- Ziemia jako obracający się, nieinercjalny układ odniesienia ( ruch dobowy z zachodu na wschód, z okresem 24 godziny).

Swobodny spadek ciała z wieży: następuje odchylenie miejsca upadku względem pionu, wyznaczonego przez siły grawitacji, o pewną wielkość ∆, największą na równiku, zerową na biegunie.

13.Praca i energia mechaniczna: praca, energia(potencjalna i kinetyczna),moc

1.Energia: jest miarą różnych rodzajów ruchu i miarą zdolności ciał do ruchu (nieodłączna cecha materii, zarówno na poziomie molekularnym jak i makroskopowym).

Każde ciało jest obdarzone energią (ma zapas energii), będącej miarą jego ruchu. Dla scharakteryzowania różnych rodzajów ruchu i różnych rodzajów i różnych rodzajów oddziaływań między ciałami, wprowadzamy różne rodzaje energii: mechaniczną, wewnętrzną, elektromagnetyczną. Jednostką miary energii jest dżul (1J=1N∙1m) lub elektronowolt (1eV= 1,6 ∙ 10^-19 J).

Wzajemne oddziaływanie między ciałami (i elementami jednego ciała) powoduje zmianę energii ciała, możemy więc opisywać to oddziaływanie jako przekazywanie energii

2.Energia mechaniczna: jej zmianę powoduje wzajemne oddziaływanie między ciałami poprzez siły. Jest sumą energii kinetycznej i energii potencjalnej.

3.Praca: to przyrost energii w procesie wykonania pracy, czyli procesie zmiany energii ciała pod wpływem działającej na nie siły. Jest wielkością skalarną, liczbowo równą iloczynowi składowej siły w kierunku wykonywanego ruchu przez drogę, przebytą w tym ruchu

W=Fs∙s

W przypadku zmiennej siły o dowolnym kierunku względem przesunięcia i dowolnej trajektorii ruchu miedzy punktami A i B, możemy uogólnić powyższy wzór

W=_A∫^B F(r)∙dr

Jednostki takie same jak w energii.

4.Energia kinetyczna: to energia każdego poruszającego się ciała mierzona pracą, jaką trzeba wykonać przy jego hamowaniu do jego całkowitego zatrzymania

Ek=mv^2/2

Z definicji pracy: EkB - EkA= _A∫^B Fwyp∙dr [Twierdzenie o pracy i energii]

Praca wykonana przez zewnętrzną siłę (wypadkową) na drodze od punktu A do punktu B równa się przyrostowi energii kinetycznej ciała. → Energia kinetyczna jest więc tzw. funkcją stanu jego ruchu ( zależy tylko od wartości początkowych i końcowych).

5.Energia potencjalna: to energia zmagazynowana przez ciało do użycia w przyszłości. Podaje się ją w postaci względnej zmiany, konkretna jej postać zależy od typu siły, z którą jest związana.

Jeżeli ciało znajduje się pod działaniem pewnej siły F, to zmianę jego energii potencjalnej ∆U obliczamy jako pracę, którą trzeba wykonać, aby przesunąć to ciało w obecności tej siły:

∆U=- _A∫^B F∙ds.

a)grawitacyjną energię potencjalną (energia potencjalna w polu sił grawitacji) możemy obliczyć następująco: U(r)-Uz=mgRz^2(1/Rz-1/r)

Uz oznacza energię potencjalną na powierzchni Ziemi(punkt odniesienia)

Gdy r ≈ Rz można skorzystać z przybliżonego wzoru: U(r)- Uz ≈mgh

Gdzie h= wysokość nad powierzchnią Ziemi (r-Rz)

b)energia potencjalna sprężystości: czyli energia np. rozciągniętej sprężyny, możemy obliczyć wykorzystując wzór na siłę sprężystą ( zgodnie z prawem Hooke'a)

F(x)= - kx

gdzie x oznacza wychylenie z położenia równowagi a k jest współczynnikiem proporcjonalności, zależnym od materiału sprężyny.

Ustalając „zerowy” poziom energii potencjalnej dla x=0 (sprężyna w położeniu równowagi, nierozciągnięta), możemy otrzymać wyrażenie na energię potencjalną sprężyny

U=kx^2/2

Wartość energii potencjalnej nie zależy od tego czy sprężyna jest rozciągnięta czy nie.

6.Moc: możemy ja zdefiniować jako tempo przekazywania energii E z jednego ciała do drugiego.

P≡dE/dt (moc chwilowa)

W szczególnym przypadku, gdy ciało porusza się z prędkością v pod działaniem siły F to moc możemy zdefiniować jako: P=F∙v

14.Zasada zachowania energii (mechanicznej)

1.Układ, w którym prawdziwa jest zasada zachowania energii w mechanice, to zamknięty układ zachowawczy (układ ciał, które działają na siebie wzajemnie siłami zachowawczymi).

[Siła zachowawcza- siła, dla której praca nie zależy od drogi, po której jest wykonywana (praca po drodze zamkniętej jest równa zeru)]

Energia mechaniczna zamkniętego układu zachowawczego nie zmienia się podczas ruchu układu: E = Ek + Ep = const (suma energii kinetycznej i potencjalnej jest stała)

2.Zasada zachowania energii może służyć do rozwiązywania zagadnień mechaniki, gdy szukamy informacji o końcowym stanie układu bez obliczania stanów pośrednich

Przykład: ciało zsuwające się bez tarcia z równi pochyłej.

15.Prawo powszechnego ciążenia

1.Wzajemne przyciąganie się ciał jest źródłem jednej z podstawowych sił w fizyce- siły przyciągania, które podlegają prawu powszechnego ciążenia (grawitacji). Prawo to podał Isaac Newton.

F=G((m1∙m2)/r^2)

Między każdymi dwoma punktami materialnymi działa siła wzajemnego przyciągania, wprost proporcjonalna do iloczynu mas tych punktów (m1 i m2) a odwrotnie proporcjonalna do kwadratu odległości między nimi.

Zapis wektorowy: F₁₂ = -G(m1∙m2/r₁₂^3)∙r₁₂

Współczynnik G, to stała grawitacji = 6,672 [Nm^2/kg^2]

2.Ciężar ciała (siła ciążenia) : siła przyciągania, jaka działa na dane ciało ze strony innego ciała. W pobliżu Ziemi będzie ona równa: P=mg , gdzie g oznacza tzw. przyspieszenie ziemskie g=G∙(Mz/Rz^2)

Siła grawitacji jest proporcjonalna do masy ciała jako miary liczebności materii, można więc by nazywać ją masą grawitacyjną. Z zasady równoważności wynika, że masa grawitacyjna jest jednocześnie masą bezwładną.

3.Pole grawitacyjne: to próba opisu wzajemnego oddziaływania ciał (na wskutek istnienia sił wzajemnego przyciągania) poprzez pewną wielkość wektorową, „niezależną” od ciała, które to pole wytwarza. Jest to inaczej przyspieszenie grawitacyjne w funkcji położenia. Można wtedy obliczyć siłę F, działającą na daną masę m, jako:

F=mg

g jest natężeniem pola grawitacyjnego, charakteryzującym siły pola grawitacyjnego

a)jednorodne- natężenie we wszystkich punktach jest jednakowe

b)centralne- jeżeli we wszystkich jego punktach wektory natężenia skierowane są wzdłuż prostych, przecinających się w jednym punkcie, nieruchomym względem dowolnego układu inercjalnego (punkt ten nazywamy środkiem sił)

c)kulisto-symetryczne- liczbowa wartość wektora natężenia zależy tylko od odległości od środka sił

Przy nałożeniu się kilku pól obowiązuje zasada superpozycji pól: natężenie pola wypadkowego równa się sumie wektorowej natężeń wszystkich pól.

Pole charakteryzuje się wielkością skalarną zwaną potencjałem pola. Jest on równy stosunkowi energii potencjalnej punktu materialnego do jego masy

V≡Ep/m

4.Pole grawitacyjne wewnątrz i na zewnątrz jednorodnej kuli:

- pole grawitacyjna na zewnątrz pustej czaszy kulistej (bądź pełnej) g=GM/R^2

- p. wewnątrz tejże czaszy g=0

- pole wewnątrz jednorodnej kuli o gęstości ρ g=(G∙M/R^2)r/R

np.pole grawitacyjne Ziemi

16.Prawa Keplera

1.I Prawo Keplera: Wszystkie planety poruszają się po orbitach w kształcie elipsy, w której ognisku znajduje się Słońce.

2.II Prawo Keplera: Linia łącząca planetę ze Słońcem zakreśla w jednakowych odstępach czasu jednakowe pola powierzchni w płaszczyźnie orbity.

Inaczej mówiąc, wielkość dS/dt , przy czym S jest polem powierzchni zakreślonej przez tę linię, jest stała.

Z II Prawa Keplera wynika, że planeta porusza się po orbicie wolniej gdy jest daleko od Słońca, a szybciej gdy jest bliżej niego. Jest to równoważne stwierdzeniu, że spełniona jest zasada zachowania momentu pędu.

Ruch ciała w polu sił centralnych:

Moment siły względem środka pola jest równy 0 : M=r × F =0

Dlatego moment pędu względem środka pola jest zachowany: K= r × (mv) = const

→ w centralnym polu sił tor ruchu tego ciała jest krzywą płaską (płaszczyzna, zawierająca wektory położenia r i prędkości v nie zmienia swej orientacji względem środka pola).

→ położenie punktu w przestrzeni określimy poprzez współrzędne biegunowe, a prędkość rozłożymy na składowe: radialną vr i poprzeczną vφ

vr=dr/dt vφ=r (dφ/dt)

Moment pędu układu zależy jedynie od prędkości poprzecznej: K=r ×(m vφ) = const

Wartość momentu pędu jest równa: K=mr^2 (dφ/dt) = const

Promień wodzący r zakreśla przy swoim obrocie o mały kąt dφ w czasie dt wycinek kołowy, którego pole jest równe: dA= ½ r^2 dφ

Stąd wielkość prędkość polowa vp = dA/dt= ½ r^2 dφ/dt

vp=K/2m= const

Przy ruchu ciała w polu centralnym jego prędkość polowa (pole zakreślane przez promień wodzący w jednostce czasu) jest stała.

3.III Prawo Keplera: Kwadrat okresu ruchu każdej planety na orbicie wokół Słońca jest proporcjonalny do sześcianu półosi wielkiej tej orbity

Zapisując drugą zasadę dynamiki Newtona dla planety znajdującej się na orbicie kołowej otrzymujemy: GMm/R^2=m(ω^2/r)

(przyspieszenie dośrodkowe)

Zamiast ω wstawiamy 2π/T i otrzymujemy trzecie Prawo Keplera:

T^2=(4π^2/GM)r^3

Da orbit eliptycznych podstawiamy zamiast r - a: półoś wielką elipsy.

Z prawa wynika, że stosunek T^2/a^3 powinien być równy dla wszystkich orbit planet krążących wokół tego samego ciała o dużej masie.

17.Środek masy i środek ciężkości układu:

1.Środek masy (środek bezwładności): środek masy układu porusza się jak punkt materialny, w którym skupiona jest cała masa układu, i na który działa siła, równa wypadkowej sił zewnętrznych przyłożonych do układu.

Każde ciało można traktować jako układ punktów materialnych. Dlatego pęd ciała możemy obliczyć jako sumę pędów wszystkich punktów materialnych ciała

p=∑mi vi= ∑mi (dri/dt)= d/dt ∑mi ri

Środkiem masy nazywamy więc punkt, którego położenie dane jest wzorem:

rs= 1/M ∑mi ri gdzie M=∑ mi

2.Środek ciężkości: jest to punkt przyłożenia wypadkowej sił ciężkości wszystkich punktów materialnych ciała. Gdy wielkość g jest jednakowa dla wszystkich punktów układu mamy:

rc=rs

18.Moment bezwładności- definicja, sens fizyczny, pojęcie tensora momentu bezwładności:

1.Moment bezwładności: jest miarą bezwładności ciała w ruchu obrotowym (analogicznie masy jako miary bezwładności w ruchu postępowym). Informuje nas jak rozłożona jest masa obracającego się ciała wokół osi jego obrotu. Jednostką momentu bezwładności I w układzie SI jest kilogram razy metr do kwadratu.

Moment bezwładności zależy nie tylko od masy obracającego się ciała, ale także od jej rozkładu. Im mniejszy jest moment bezwładności ciała, tym łatwiej jest wprawić je w ruch obrotowy.

I=∑mi ri^2

W przypadku ciała o bardzo nieregularnych kształtach sumowanie zastąpimy całkowaniem.

r- odległość każdej cząstki od osi obrotu

2.Tensor momentu bezwładności:

Rozważając obrót ciała o dowolnym kształcie wokół osi przechodzącej przez początek układu współrzędnych.

Moment pędu tego ciała: K≡ ∑ri×(mi vi)= ∑ mi ri × (ω×ri)= ∑ mi [ωri^2- ri(ri∙ω)]

Wszystkie punkty mają tą samą prędkość kątową, możemy zapisać więc powyższe równanie wektorowe jako układ trzech równań dla poszczególnych składowych ω

Kx≡ωx∑mi ri^2 - ∑ mi xi (mi∙ω) analogicznie dla y i z

|Ixx Ixy Ixz| |ωx|

[Kx, Ky, Kz]= | Iyx Iyy Iyz | ∙ |ωy|

|Izx Izy Izz| |ωz|

Macierz z prawej strony równania to tensor bezwładności a jego elementy nazywamy współczynnikami bezwładności lub momentami bezwładności.

19.Twierdzenie Steinera (twierdzenie o osiach równoległych):

1.Definicja: Moment bezwładności ciała I względem dowolnej osi O równa się momentowi bezwładności I' tego ciała względem innej, równoległej do niej osi O', powiększonemu o iloczyn masy tego ciała przez kwadrat odległości między tymi osiami.

I = I' + md^2

Zakładamy, że znamy moment bezwładności ciała względem pewnej osi obrotu, ale ciało obraca się wokół innej, równoległej do niej.

2.Wniosek: Gdy środek masy ciała oddala się od osi obrotu, to moment bezwładności ciała względem tej osi wzrasta.

20.Moment pędu i zasada zachowania momentu pędu

1.Moment pędu: Moment pędu K cząstki o pędzie p, masie m i prędkości liniowej v jest wielkością wektorową, definiowaną względem pewnego układu odniesienia (zwykle początku układu współrzędnych) i jest równy:

K≡ r × p = m (r × v)

Długość wektora K wynosi: K= r m v sinφ = rp gdzie φ jest kątem między wektorami r i p

Kierunek wektora K wyznaczamy za pomocą reguły prawej dłoni dla iloczynu wektorowego.

2.Zasada zachowania momentu pędu: Moment pędu K układu pozostaje stały, gdy wypadkowy zewnętrzny moment siły, działający na układ jest równy 0:

K=const (układ izolowany)

Kpocz= Kkonc

dK/dt = M (M=0)→dK/dt=0 → K=const

Jeśli siły zewnętrzne dają moment względem nieruchomej osi równy zeru, to moment pędu względem tej osi podczas ruchu nie zmienia się

Słuszność tej zasady wykazano także w przypadkach, w których nie obowiązują zasady dynamiki Newtona.

21.Hydrostatyka płynów: prawa Pascala i Archimedesa

1.Hydrostatyka: zajmuje się opisem statycznych zależności między ciśnieniami w cieczach

2.Płyn: po tą nazwą rozumiemy ciecze i gazy - to substancja zdolna do przepływu; gdy umieścimy go w naczyniu przybiera jego kształt

3.Prawo Pascala: mówi, że w zamkniętej objętości nieściśliwego płynu zmiana ciśnienia jest przenoszona bez zmiany wartości do każdego miejsca w płynie i do ścian zbiornika

W obecności sił ciężkości dla cieczy nieściśliwej przybiera ogólniejszą postać:

p= po + ρgh

gdzie po jest ciśnieniem zewnętrznym przyłożonym do górnej powierzchni cieczy, ρ jest gęstością cieczy a odległością od górnej powierzchni jest h

p Ziemi =1,01 ∙10^5 N /m^2 ≡1atm

- Praktycznym zastosowaniem Prawa Pascala jest wykorzystanie go do budowy barometrów( przyrządów służących do pomiaru cięsnienia)

- Prasa hydrauliczna ∆p=Fwej/Swej= Fwyj/Swyj

4.Prawo Archimedesa: mówi, że na ciało zanurzone w cieczy działa siła wyporu,skierowana przeciwnie do siły ciężkości, równa liczbowo ciężarowi wypartej cieczy.

Zgodnie z prawem Pascala, jeśli zanurzymy w cieczy ciało stałe, to na poszczególne części tego ciała będzie działać różne ciśnienie, w zależności od tego na jakiej głębokości znajduje się dana część tego ciała.

Siła wypadkowa zwana siłą wyporu Fwyp= Fwgórę - Fwdół= ρgdS

S-pole powierzchni, na którą działa siła, d - wysokość ciała

Fw= mp ∙ g mp- masa wypartego płynu

22.Napięcie powierzchniowe:

1.Napięcie powierzchniowe: zjawisko występujące na granicy faz (ciało stałe, ciecz, gaz) jako efekt różnic w wielkościach sił oddziaływań międzycząsteczkowych dla poszczególnych faz.

2.Faza termodynamiczna: część układu fizycznego oddzielona od innych powierzchniami, na których zachodzi skokowa zmiana własności fizycznych lub chemicznych.

3.Miarą napięcia powierzchniowego jest praca, jaką trzeba wykonać, aby zwiększyć powierzchnię cieczy o jednostkę.

η=dW/ds.= dF/dl

4.Przykłady:

-kapilara- bardzo cienka rurka, w której praktycznie cała przepływająca ciecz znajduje się w polu oddziaływania sił związanych jej ściankami i cieczy bezpośrednio przylegającej do ścianek

-naczynia włosowate: krew dociera do najodleglejszych tkanek bez konieczności stosowania wysokich ciśnień

-menisk :

*wklęsły (powierzchnia cieczy w pobliżu ścianek zakrzywia się w górę )- występuje gdy siły oddziaływania między cząsteczkami cieczy i ścianek są większe od sił oddziaływania między cząsteczkami cieczy

*wypukły (powierzchnia cieczy w pobliżu ścianek zakrzywia się w dół _- występuje gdy siły oddziaływania między cząsteczkami cieczy i ścianek są mniejsze od sił oddziaływania między cząsteczkami cieczy

23.Hydrodynamika: przepływ płynu, prawa: ciągłości, Bernoullego

1.Hydrodynamika: opisuje własności dynamiczne między ciśnieniami w cieczach

2.Przepływ płynu:

- przepływ płynu rzeczywistego jest bardzo złożony, omawiamy więc przepływ płynu doskonałego

-założenia związane z przepływem płynu abyśmy mogli mówić o przepływie płynu doskonałego:

* przepływ ustalony (laminarny) - prędkość poruszającego się płynu w każdym wybranym punkcie nie zmienia się z upływem czasu, zarówno do wartości jak i kierunku

*przepływ nieściśliwy - płyn doskonały jest nieściśliwy, czyli ma stałą gęstość

*przepływ nielepki - lepkość jest miarą oporu, jaki stawia płyn jego przepływowi

*przepływ jest bezwirowy- żaden z fragmentów płynu nie porusza się wokół osi przechodzącej przez swój środek masy

Do badania charakteru przepływu płynów służą m.in. tunele aerodynamiczne, w których dzięki wskaźnikom widoczne są linie prądu.

3.Prawo ciągłości:

-dotyczy przepływu płynów przez ośrodek o zmiennym przekroju

- Zakładając że w czasie ∆t do rury wpływa płyn o objętości ∆V, płyn jest nieściśliwy, więc na końcu rury musi wypłynąć z tym samym czasie płyn o takiej samej objętości V.

Zapisując równanie dla lewego i prawego końca rury otrzymujemy:

∆v = S1v1∆t = S2v2∆t

Czyli S1v1=S2v2 (Równanie ciągłości dla przepływu płynu doskonałego)

-Przykład:

* Gdy zasłonimy część otworu wylotowego węża ogrodowego prędkość wypływającej wody zwiększa się

*Struga prądu - umowna rura ograniczona przez linie prądu

- Inny sposób zapisu: Rv = Sv = const

Rv- strumień objętościowy ( m^3/s)

4.Prawo Bernoullego:

- Równanie Bernoullego stosujemy tylko do przepływu płynu doskonałego

- p+1/2 (ρv^2) + ρgh = const

h- poziom, na którym wchodzi/wychodzi płyn

- Interpretacja: gdy element zbliża się do wąskiego miejsca w rurze, panujące za nim duże ciśnienie powoduje przyspieszenie jego ruchu, w związku z czym w wąskim miejscu rury prędkość przepływu jest duża. Gdy natomiast element płynu zbliża się do szerokiego miejsca w rurze, panujące przed nim duże ciśnienie powoduje zwolnienie ruchu, w związku z czym w szerokim miejscu rury prędkość przepływu jest mała.

-Innymi słowy, w miejscach, w których linie prądu są ułożone stosunkowo blisko siebie (tzn. w miejscach, w których prędkość przepływu jest stosunkowo duża), ciśnienie płynu jest stosunkowo małe i na odwrót.

24.Termodynamika fenomenologiczna: wielkości w opisie makroskopowym

1.Termodynamika: dział fizyki, który zajmuje się energią termiczną (energią wewnętrzną) układu

2.Termodynamika fenomenologiczna: dziedzina termodynamiki, w której przyjmuje się założenie ciągłości zjawisk zachodzących we wnętrzu układów makroskopowych i nie uwzględnia się złożoności ich mikroskopowej budowy.

3. Wielkości w opisie makroskopowym:

*objętość - jest miarą przestrzeni, jaką zajmuje dane ciało w przestrzeni trójwymiarowej. Jednostką jest m^3.

*ciśnienie - definiujemy jako stosunek siły, jaką gaz lub ciecz wywiera na ściankę naczynia, w którym się znajduje, do powierzchni tej ścianki

p≡∆F/∆S

Jednostką ciśnienia jest Pascal [Pa] 1Pa=1N/m^2 . Inną jednostką jest atmosfera - przybliżona wartość średnia ciśnienia na poziomie morza 1atm= 1,01 ∙10^5 [Pa].

Do jego mierzenia służy np. barometr.

*temperatura- jej definicja w ramach termodynamiki klasycznej (makroskopowej) to parametr opisujący stan równowagi termicznej układu

- do jej pomiaru wykorzystuje się urządzenia bazujące na 0 zasadzie termodynamiki (jeżeli ciało 1 i ciało 2 znajdują się w równowadze termodynamicznej i ciała 2 i 3 są również w takiej równowadze, to ciała 1 i 3 są także w tej samej równowadze termodynamicznej w której byłyby, gdyby były w kontakcie ze sobą)

4.Skale temperatur:

- Skala Kelvina (bezwzględna skala temperatur): oparta jest na definicji punktu „0” jako „zera” energii kinetycznej, kiedy ustaje wszelki ruch cząsteczek, i jednostce temperatury - kelwinie (K) - równym stopniowi Celsjusza. „Zero bezwzględne” to ok. -273 stopnie w

bardziej znanej na co dzień skali Celsjusza.

- Skala Celsjusza- została stworzona na bazie dwóch punktów, charakterystycznych dla wody: temperaturze zamarzania (przyjętej za „0”) i temperaturze wrzenia (jako „100”). Jednostką jest więc 1/100 tego przedziału, zwana stopniem Celsjusza (ºC).

- krajach anglosaskich używana jest skala Fahrenheita. Jeden stopień w tej skali równa się 5/9 stopnia Celsjusza.

5.Termometry:

-budowa termometrów oparta jest na definicji makroskopowej, wiążącej inne mierzalne parametry gazu doskonałego (ciśnienie i objętość) z szukaną temperaturą. Bądź na pomiarze innych wielkości fizycznych, których wartość zależy od temperatury

*termometry objętościowe: związane są ze zmianą wymiarów ciała ze zmianą temperatury (rozszerzalność liniowa) np. termometry rtęciowe

*termometry gazowe stałej objętości: bazują na pomiarze zmian ciśnienia ze zmianą temperatury.

*termorezysty: to elementy elektryczne, które mierzą zmiany temperatury poprzez pomiar związanej z nią zmiany oporu przewodnika bądź półprzewodnika.

25.Zasady termodynamiki i ich wybrane zastosowania: 0,1,2

1.”0” zasada termodynamiki: jeżeli ciało 1 i ciało 2 znajdują się w równowadze termodynamicznej i ciała 2 i 3 są również w takiej równowadze, to ciała 1 i 3 są również w takiej samej równowadze termodynamicznej, w której byłyby będąc w kontakcie ze sobą.

[równowaga termodynamiczna- stan, w którym wszystkie makroskopowe parametry układu są stałe w czasie]

Zastosowanie: wykorzystanie tej zasady w urządzeniach służących do pomiaru temperatury.

2.”1” zasada termodynamiki: Energia wewnętrzna układu wzrasta, jeżeli układ pobiera energię w postaci ciepła i maleje, kiedy wykonuje pracę.

dEw= ∆Q -∆W

Różnica Q - W jest dla wszystkich procesów jednakowa, jej wartość zależy jedynie od stanu początkowego i stanu końcowego, ale nie zależy od sposobu przeprowadzenia układu między stanami

Energia wewnętrzna układu wzrasta, jeżeli układ pobiera energię w postaci ciepła Q i maleje, kiedy wykonuje on pracę W.

Energia może być przekazywana układowi lub zabierana w postaci ciepła i pracy.

I zasada termodynamiki działa na układy, które nie są izolowane ( pobierają lub oddają energię z zewnątrz).

Przykłady: przemiana adiabatyczna(nie wymienia energii w postaci ciepła z otoczeniem), izochoryczna, izotermiczna, izobaryczna (?)

3.”2” zasada termodynamiki:

-nie można zbudować perpetuum mobile II rodzaju ( cykliczna maszyna, która zamienia energię cieplną na pracę mechaniczną bez wzrostu całkowitej entropii”

-gdy dwa ciała znajdą się w kontakcie termicznym, wówczas ciepło będzie przepływało z cieplejszego do chłodniejszego

-żadna cykliczna maszyna cieplna pracująca między temperaturami T1 i T2 nie może mieć sprawności większej niż (T1-T2)/T1

- w układzie zamkniętym entropia wzrasta w przemianach nieodwracalnych i nie zmienia się przemianach odwracalnych. Entropia nigdy nie maleje. ∆S =› 0

(entropia- miara stopnia nieuporządkowania układu, funkcja stanu określająca kierunek przepływu procesów samorzutnych)

26.Równanie stanu gazu doskonałego i rzeczywistego

1.Gaz doskonały: gaz, który spełnia następujące warunki:

- objętość cząsteczek jest o wiele mniejsza, niż objętość zajmowana przez gaz

- zasięg sił, działających miedzy dwiema cząsteczkami, jest o wiele mniejszy niż średnia odległość między nimi.

Gaz doskonały - zbiór „małych, twardych kulek”, które sprężyście zderzają się ze sobą i ze ściankami otaczającego go naczynia

2. Równanie stanu gazów doskonałych (równanie Clapeyrona):

pV = NkT = nRT

N-liczba cząsteczek gazu w jednostce objętości n- liczba moli gazu

R- stała gazowa 8,31J/(mol·K) k- stała Boltzmana 1,38·10^-23 J/K

3. Gazy rzeczywiste (prawo van der Walsa) nie zachowuje się zgodnie z prawami ustalonymi dla gazu doskonałego

(p + a/v^2)(V-b)= RT

Stałe a i b wyznaczane są doświadczalnie.

27.Pojęcia energia wewnętrzna, entropia (interpretacja makro- i mikroskopowa)

1.Energia wewnętrzna: energia wewnętrzna układu termodynamicznego jest to całkowita energia układu (jego cząstek i ich wzajemnego oddziaływania), którą posiada on w warunkach równowagi termodynamicznej

2.Entropia: jest miarą nieuporządkowania układu cząstek. Im większy jest stan nieporządku położeń i prędkości w układzie tym większe prawdopodobieństwo, że układ będzie w tym

stanie.

Przykład zwiększenia się nieuporządkowania:

- rozprężanie swobodne

- przepływ ciała do wyrównania temperatur

Definicja entropii: S = k lnω ω- prawdopodobieństwo, że układ jest w danym stanie

Układ poszukuje stanów o większym prawdopodobieństwie, ∆S =› 0

*Przemiany nieodwracalne powodują zawsze wzrost entropii

*Entropia jest funkcją stanu - jej wartość zależy tylko od stanu układu

*Entropia układu zamkniętego wzrasta w przemianach nieodwracalnych i nie zmienia się w przemianach odwracalnych. Entropia nigdy nie maleje.

[ukł.zamknięty- nie wymienia z otoczeniem materii, jedynie energię].

28.Przemiany gazu doskonałego. Praca w różnych przemianach.

1.Przemiana izochoryczna: V = const

Prawo Charlesa - p ≈ T

W= ∫ p dv = 0

2.Przemiana izobaryczna: p=const

Prawo Gay - Lussaca - V ≈ T

W= p ∆V

3.Przemiana izotermiczna: T=const

Prawo Boyle'a - Mariotte'a pV=const

W=∫ p dv = ∫ nRT/V ∙ Dv = nRT ln Vkonc/Vpoczatkowe

4.Przemiana adiabatyczna: nie zachodzi wymiana ciepła z otoczeniem

Równanie adiabaty: pV^γ = const gdzie γ= Cp/Cv >1

(Ciepła molowe przy stałym ciśnieniu i objętości)

Inna postać równania adiabaty: TV^γ-1= const

dW= -p Dv

29.Silniki cieplne

1.Silnik cieplny: to urządzenie, które ze swego otoczenia pobiera energię w postaci ciepła i wykonuje użyteczną pracę. Substancja roboczą w silnikach może być woda (w postaci pary wodnej), benzyna itd.

2.Silnik idealny: wszystkie procesy są odwracalne i nie ma strat energii związanych z tarciem bądź turbulencjami η=1 [nie istnieje]

3.Silnik Carnota:

-cykl przemian substancji roboczej: dwie izotermy i dwie adiabaty

-sprawność: η= |W|/|Qg|= (|Qg|-|Qz|)/ |Qg| = 1- (Tz/Tg)

4.Silnik Sterlinga:

-cykl przemiany substancji roboczej: dwie izotermy, dwie izochory

5.Sprawność silnika cieplnego:

η= energia uzyskana/energia dostarczona

30.Zjawiska termoelektryczne:

1.Zjawiska termoelektryczne: to efekt bezpośredniej transformacji napięcia elektrycznego występującego między dwoma punktami układu ciał na różnice temperatur między tymi punktami, lub odwrotnie: różnicy temperatur na napięcie elektryczne. W zależności od kierunku transformacji zjawiska dzieli się na:

- zjawisko Seebecka: powstanie siły termoelektrycznej w zamkniętym obwodzie składającym się z dwóch różnych metali, o ile miejsca styku tych metali znajdują się w różnych temperaturach,

- zjawisko Peltiera: gdy prąd elektryczny przepływa przez miejsce złączenia dwóch różnych metali, to zależnie od kierunku przepływu złącze to nagrzewa się lub oziębia

- zjawisko Thomsona- nagrzewanie lub oziębianie pod wpływem przepływu prądu występujące również w jednorodnym przewodniku, którego końce znajdują się w różnych temperaturach

31.Elementy termodynamiki statystycznej: idee opisu statystycznego, mikroskopowa interpretacja temperatury:

1.Idee opisu statystycznego:

- powrót do podejścia mikroskopowego i wyprowadzenia w jego ramach zależności między parametrami termodynamicznymi

2.Mikroskopowa interpretacja temperatury:

- w teorii kinetycznej temperaturę definiujemy jako:

T≡ (2/3k) m<v^2>/2 = (2/3k) K

K- jest średnią energią kinetyczną przypadającą na jedną cząsteczkę gazu

Z teorii kinetycznej wynika, że temperatura jest tym wyższa, im szybciej poruszają się cząsteczki danego ciała. Temperatura jest wprost proporcjonalna do średniej energii kinetycznej cząsteczek ciała.

32.Funkcja rozkładu Maxwella: co to jest? założenia, wynik (wykresy)

1.Rozkład Maxwella: prawo pozwalające określić, jaka liczba cząstek dn z całej ilości n₀ cząstek gazu doskonałego w jednostce objętości (n₀₌ N/V) ma w danej temperaturze prędkości w przedziale od v do v+dv

2.Założenia:

-spełnione są zasady zachowania: liczby cząsteczek, energii, pędu, momentu pędu, ładunku.

- wszystkie procesy fizyczne w układzie przebiegają w sposób ciągły w czasie i przestrzeni

- obliczenia statystyczne przeprowadzono przy założeniu rozróżnialności cząstek;

(por. kombinatoryka w rachunku prawdopodobieństwa);

- każda cząstka może mieć dowolne wartości współrzędnych i prędkości, niezależnie od wartości współrzędnych i prędkości innych cząstek; (a więc w szczególności prawdopodobieństwo znalezienia się cząstki w danej objętości przestrzeni jest niezależne od tego, ile innych cząstek tę „komórkę” przestrzeni zajmuje!)

3.Korzystając z rozkładu Maxwella możemy wyliczyć:

Prędkość najbardziej prawdopodobną, prędkość średnią kwadratową, prędkość średnią

4. Wynik: maksimum krzywej przesuwa się wraz ze wzrostem temperatury w kierunku większych prędkości - przy ogrzewaniu gazu udział cząsteczek obdarzonych małymi prędkościami zmniejsza się

33.Zasada ekwipartycji energii cieplnej

1.Zasada ekwipartycji energii: prawo równomiernego rozkładu energii między stopnie swobody: na każdy stopień swobody cząsteczki średnio przypada jednakowa energia kinetyczna równa (kT/2)

2. Liczba stopni swobody: to najmniejsza możliwa liczba współrzędnych (liczba współrzędnych niezależnych), które musimy podać, aby jednoznacznie określić położenie ciała w przestrzeni.

Jeżeli cząsteczka obdarzona jest i stopniami swobody, to jej średnia energia potencjalna wyrażona jest wzorem: ek= i/2 kT

3.W gazie doskonałym nie ma oddziaływań między cząsteczkami, więc energia potencjalna jest równa 0. Dlatego energia wewnętrzna 1 mola gazu doskonałego równa się sumie energii kinetycznych Na cząstek

U= i/2 k T Na = i/2 RT

[Temperatura jako miara energii wewnętrznej cząsteczek]

34. Ruch okresowy: drgania, drgania okresowe, drgania harmoniczne (definicje, definicje podstawowych wielkości opisujących drgania, równanie drgań harmonicznych, przykłady).

1.Drgania- ruch (lub stan), który charakteryzuje się powtarzalnością w czasie wielkości fizycznych, określających ten ruch lub stan (np. położenie, prędkość).

2.Drgania okresowe - (periodyczne) powtarzanie zachodzi zawsze po tym samym czasie T, zwanym okresem (okres- czas, w jakim wykonywane jest jedno pełne drganie)

3.Drgania harmoniczne- jest to ruch okresowy opisywany sinusoidalna funkcją czasu. Położenie ciała opisuje następujący wzór: x(t)=A sin (ωt +φ)

A- amplituda, dodatnia stała, której wartość zależy od tego, jak silnie wykonano drgania;

Maksymalna zmiana względem położenia równowagi

φ- faza początkowa ω - częstość kołowa [rad/s] (ωt +φ)- faza drgań [radiany]

* prędkość w ruchu harmonicznym opisana jest następująco: v(t)=Aω cos(ωt +φ)

* przyspieszenie : a(t)= -A ω^2 sin (ωt + φ)

Również funkcje harmoniczne

* energia w ruchu harmonicznym Ep=kx^2/2

*częstotliwość drgań: f=1/T= ω/2π [Hz]

*ruch harmoniczny to taki, dla którego F= -kx (Siła jest proporcjonalna do wychylenia i przeciwnie do niego skierowana (Prawo Hooke'a) F- siła harmoniczna

4.Drgania harmoniczne - przykłady:

*wahadło matematyczne - punkt materialny zawieszony na nieważkiej i nierozciągliwej nici

g(t)= -g sin φ T= 2π√l/g

* wahadło fizyczne - ciało doskonale sztywne, które pod działaniem własnego ciężaru waha się dookoła osi poziomej, nie przechodzącej przez środek ciężkości ciała

* sprężyna-

Prawo Hooke'a F= -kx

Równanie ruchu: d^2x/dt^2 = -k/m x(t)

Okres drgań: 2π√k/m

*obwód LC ( z cewką i kondensatorem) T=2π√LC

35.Ruch okresowy: tłumiony, wymuszony

1.Drgania tłumione: jeżeli ruch oscylatora słabnie na skutek działania sił zewnętrznych, to taki oscylator nazywamy tłumionym, a jego drgania nazywamy tłumionymi.

Siły zewnętrzne to np.: woda , opory powietrza.

Oscylator- urządzenie lub układ fizyczny wykonujący ruch drgający

*Siły oporu są proporcjonalne do prędkości ciała: Foporu= -r v = -r (dx/dt)

*Ogólne równanie drgań tłumionych: x(..) +2βx(.) +ωo^2x=0

(straty energii na oporze ośrodka, proporcjonalne do pierwszej pochodnej zmiany położenia,

czyli prędkości).

*Tłumienie krytyczne - minimalna wartość tłumienia, przy której ruch jest aperiodyczny (nieokresowy)

* Drgania gasnące są drganiami nieokreślonymi nigdy nie powtarzają się największe wartości wychylenia, prędkości, przyspieszenia. Dlatego tylko umownie można nazwać ω częstością kątową - w tym sensie, że wskazuje ona, ile razy w ciągu π sekund drgający układ przechodzi przez położenie równowagi!

*Współczynnik tłumienia mówi o stosunkach kolejnych drgań gasnących

*Oznaczmy przez τ odstęp czasu, w ciągu którego amplituda drgań zmniejszy się -krotnie. Wtedy: βτ =1 . Czyli: współczynnik tłumienia β jest wielkością fizyczną równą odwrotności odstępu czasu τ, w ciągu którego amplituda zmniejsza się e-razy. Czas τ nazywamy czasem relaksacji.

2. Drgania wymuszone: występują wtedy, gdy na układ działamy siłą dodatkową - okresową siłą wymuszającą F: F(t)= Fo cos(ωt)

*Amplituda A ustalonych drgań wymuszonych jest wprost

proporcjonalna do amplitudy siły wymuszającej Fo i odwrotnie proporcjonalna do masy m układu oraz zmniejsza się wraz ze wzrostem współczynnika tłumienia β.

*„Faza początkowa” ma teraz sens różnicy faz między amplitudą drgań wymuszonych A i amplitudą siły wymuszającej Fo (ściślej: ponieważ użyliśmy funkcji „cosinus” do opisu siły wymuszającej i funkcji „sinus” do opisu drgania x(t), to szukaną różnicą faz będzie:

α=φo - π/2

*możemy zauważyć, że w przypadku braku tłumienia (β=0), gdy częstość ω siły wymuszającej F równa jest częstości drgań własnych układu ωo, amplituda ta rośnie do nieskończoności!

36.Pojęcie rezonansu (mechanicznego):

1.Rezonans: zjawisko polegające na przepływie energii pomiędzy kilkoma (najczęściej dwoma) układami drgającymi. Warunkami koniecznymi do zajścia rezonansu są: jednakowa lub zbliżona częstotliwość drgań własnych (lub swobodnych) układów, istnienie mechanicznego połączenia między układami.

2. Gdy β ≠ 0 , maksimum wyrażenia na amplitudę A uzyskamy gdy: ω=√ (ωo^2 - 2 β^2)

Zajście takiego warunku nazywamy rezonansem.

3.Przykład: obwód elektryczny

37. Fale mechaniczne: definicja, równanie falowe, rodzaje i przykłady fal.

1.Fale mechaniczne: (Fala- falą nazywamy każde rozprzestrzeniające się w przestrzeni zaburzenie [odkształcenie]. Fala jest zależna od x i t. Przenoszą energię, ale nie transportuja materii. Mogą rozchodzić się w ośrodkach materialnych). Fala mechaniczna, to taka, która rozchodzi się w ośrodkach sprężystych tj.: woda, powietrze czy skała. Podlegają zasadom dynamiki Newtona i mogą występować jedynie w ośrodkach materialnych. Są to na przykład fale na wodzie, fale dźwiękowe, fale sejsmiczne

2.Rodzaje fal mechanicznych:

-fala poprzeczna: gdy drgania zachodzą w kierunku prostopadłym do kierunku rozchodzenia się fal

-fala podłużna: drgania zachodzą w kierunku równoległym do kierunku rozchodzenia się fal

[poprzeczna i podłużna są falami biegnącymi]

-fala stojąca: taki rodzaj drgań ośrodka, który charakteryzuje się regularnym występowaniem na przemian miejsc, gdzie amplituda drgań jest równa zeru (węzły) i gdzie jest maksymalna - równa 2A (strzałki).

Generowanie fal stojących: Przykład: płaska, prostokątna membrana o bokach a i b - można na niej wzbudzić falę stojącą tylko taką, która opowiada ułożenie się na każdej krawędzi całkowitej wielokrotności połowy odpowiadającej jej długości fali - figury Chladniego.

2. Równanie falowe:

δ^2 ψ/δr^2= 1/v^2 (δ^2ψ/δ t^2)

3.Długość fali: długością fali λ nazywamy odległość (mierzoną równolegle do kierunku rozchodzenia się fali) między kolejnymi powtórzeniami kształtu fali.

38. Fale mechaniczne: prędkość fazowa i grupowa; zasada superpozycji; interferencja

1.Prędkość fazowa: (vf) prędkość rozchodzenia się stałej fazy ( każdej fali składowej osobno)

V(f)= ωi/ki k- liczba falowa : 2π/λ

2.Prędkość grupowa: (vg) prędkość rozchodzenia się paczki fal sinusoidalnych o zbliżonych częstościach (prędkość „grzbietu obwiedni”)

Paczka fal (pakiet fal)- fala skupiona w ograniczonym obszarze przestrzeni

3.Zasada superpozycji: (ogólnie - gdy równocześnie pojawia się kilka efektów, ich wypadkowy skutek jest sumą skutków poszczególnych efektów)

Zakładając, że dwie fale biegną równocześnie wzdłuż tej samej napiętej liny. Niech yi(x, t) i y2(x, t) będą przemieszczeniami tej liny spowodowanymi przez każdą z fal osobno. Przemieszczenie liny w sytuacji, gdy fale nakładają się, będzie ich sumą algebraiczną

y'(x,t) = y1(x,t) +y2(x,t)

Gdy impulsy nakładają się, wypadkowy impuls stanowi ich sumę.

4.Interferencja:

-definicja: zjawisko nakładania się dwóch lub więcej fal

- wypadkowa faza zależy od tego jaka jest względna faza obu fal, czyli od tego o ile jedna fala jest przesunięta wobec drugiej. Gdy fale są dokładnie takie same (zgodne w fazie), to przemieszczenie wypadkowe jest dwukrotnie większe niż dla każdej z fal osobno. Jeżeli mają one fazy zupełnie niezgodne (grzbiety jednej fali pokrywają się z „dolinami” drugiej),pochodzące od nich przemieszczenia znoszą się w każdym punkcie ( następuje całkowite wygaszenie fali)

- gdy dwie fale sinusoidalne o takich samych amplitudach i długościach fali biegną w tym samym kierunku, interferują ze sobą, dając wypadkową falę sinusoidalną biegnącą w tym samym kierunku

-obie fale mają takie same ω, takie same k i A,obie biegną w dodatnim kierunku osi x z taką samą prędkością, różnią się jedynie w fazie o stały kąt φ zwany przesunięciem fazowym.

39.Fale dźwiękowe

1. Fale dźwiękowe (akustyczne) są rodzajem fal sprężystych, rozchodzących się w ciągłym ośrodku odkształceń objętościowych lub odkształceń postaci (w ciałach stałych). W powietrzu są przykładem fal podłużnych, polegających na rozchodzeniu się zagęszczeń i rozrzedzeń

powietrza.

2. Równanie falowe: ( ………………….)

3. Natężenie fali dźwiękowej: I = P/S=1/2 ρv ω^2 sm

sm- amplituda fali P- moc (szybkość przenoszenia energii)

Ludzkie ucho odbiera dźwięk o amplitudzie od 10^-5 m do 10^-11 m, czyli stosunek natężeń dla tych dwóch granic wynosi 10^12

Stąd zamiast natężenia fali dźwiękowej używa się głośności dźwięku β

β=(10dB)logi/Io

Io = 10^-12 [W/m^2) standardowe natężenie odniesienia

---