Nr ćwicz. 220	Data: 29.10.97	Krzsztof Byrwa	Wydział Elektryczny	Semestr: I	Grupa: T1
prowadzący: mgr. M. Andrzejewska					Przygotowanie:	Wykonanie:	Ocena ostat.:

Temat: Wyznaczanie stałej Plancka i pracy wyjścia na podstawie zjawiska fotoelektrycznego.

Wstęp teoretyczny:

W ciałach stałych, będących przewodnikami, elektrony walencyjne są związane z macierzystymi atomami - poruszają się one w sieci krystalicznej tworząc tzw. gaz elektronowy. Swobodny ruch elektronów w kryształach metalicznych wynika z rozkładu energii potencjalnej. W wyniku wzajemnego oddziaływania atomów bariery potencjałów oddzielające sąsiednie atomy ulegają obniżeniu do wartości mniejszej niż całkowita energia elektronu i nie stanowią przeszkody w ruchu elektronów (rys.1).

Atomy znajdujące się na powierzchni kryształu mają sąsiadów tylko od strony wnętrza i dlatego energia potencjalna tych atomów jest nieco inna niż w głębi kryształu. energia potencjalna na powierzchni jest większa więc, powierzchnia stanowi barierę dla elektronów, dzięki której nie mogą one opuścić kryształu. Obrazowo można powiedzieć, że elektrony są uwięzione w „pudle” potencjału - mogą się swobodnie poruszać w jego wnętrzu, lecz nie mogą przejść przez jego ściany.

Opuszczenie metalu przez elektron (pokonanie bariery potencjału U_o ) jest możliwe jeśli uzyska on na to dodatkową energię o wartości przynajmniej e U_o. Ta energia nazywa się pracą wyjścia. Źródłem energii mogą być:

a) podwyższona temperatura - zachodzi wówczas zjawisko termoemisji;

b) silne pole elektryczne - emisja polowa;

c) bombardowanie cząsteczkami o dostatecznie dużej energii kinetycznej, oraz

d) oświetlenie kryształu.

W ostatnim przypadku mamy do czynienia ze zjawiskiem fotoelektrycznym. Wybicie elektronu z metalu przez foton zachodzi tylko wtedy, gdy energia fotonu hν jest równa lub większa od pracy wyjścia W.

Przemiany energii w zjawisku fotoelektrycznym opisuje równanie Einsteina

(1).

gdzie : h - stała Plancka równa 6,62 * 10^-34 [Js] , ν - częstotliwość fali świetlnej , W - praca wyjścia , m - masa elektronu , v - jego prędkość poza metalem.

Zjawiskiem fotoelektrycznym rządzą następujące prawa:

a) Fotoelektrony pojawiają się natychmiast po naświetleniu metalu (po czasie 3*10^-9s).

b) Prąd fotoelektryczny, czyli ilość emitowanych w jednostce czasu elektronów jest proporcjonalna do oświetlenia.

c) Energia fotoelektronów nie zależy od oświetlenia, jest ona proporcjonalna do częstotliwości drgań fali świetlnej.

Powyższe własności mogą być wyjaśnione tylko na gruncie teorii korpuskularnej (kwantowej) światła.

Zjawisko fotoelektryczne znalazło zastosowanie praktyczne w fotokomórkach Budowę fotokomórki pokazano na (rys.2). Składa się ona z bańki szklanej, której tylna ścianka pokryta jest wewnątrz warstwą metalu o małej pracy wyjścia . W środku bańki znajduje się pętla z drutu stanowiąca anodę . W zależności od zawartości bańki fotokomórki mogą być próżniowe lub gazowane.

W fotokomórce próżniowej całkowity prąd stanowią elektrony wybite z katody i przyciągnięte przez anodę. Natężenie prądu jest stosunkowo małe.

Większe natężenie prądu uzyskuje się w fotokomórkach gazowych, wypełnionych niewielką ilością gazu szlachetnego, w których fotoelektrony pierwotne mogą jonizować atomy gazu zwiększając w ten sposób ilość nośników prądu.

Elektrony wybite z katody fotokomórki próżniowej tworzą chmurę elektronową odpychające następne elektrony dążące w jej kierunku. W miarę wzrostu napięcia na anodzie chmura zostaje coraz silniej przyciągana do anody, aż przy pewnym napięciu każdy fotoelektron dochodzi do anody. Mimo dalszego wzrostu napięcia nie następuje dalszy wzrost fotoprądu - osiągnięty został stan nasycenia. Aby uzyskać większy fotoprąd trzeba zwiększyć oświetlenie.

Prąd fotoelektryczny płynie nawet wtedy, gdy między anodą i katodą nie ma napięcia. Dzieje się tak dzięki energii kinetycznej posiadanej przez elektrony w momencie wybicia z metalu. Całkowity zanik prądu można uzyskać przykładając napięcie o przeciwnej polaryzacji, tzn. potencjał niższy na anodę. Jeżeli napięcie ma odpowiednią wartość zwaną potencjałem hamującym V_h , to następuje całkowite zahamowanie elektronów - ich energia kinetyczna zostaje zużyta na wykonanie pracy przeciwko polu elektrycznemu

(2)

Uwzględniając powyższy związek możemy przekształcić równanie (1) do postaci

(3)

Na podstawie wykresu zależności V_h = f (ν) można znaleźć stałą Plancka h oraz pracą wyjścia W , gdyż tangens kąta nachylenia prostej, opisanej równaniem (3) wynosi h/e, a punkt przecięcia osi rzędnych ma wartość -W/e.

Zasada pomiaru:

1. Przyrządy połączyć zgodnie ze schematem:

1 - Zasilacz oświetlenia

2 - Żarówka

3 - Przysłona

4 - Filtr

5 - Fotokomórka

6 - Mikroamperomierz cyfrowy

7 - Woltomierz cyfrowy

8 - Zasilacz

2. Nastawić filtr przepuszczający najkrótszą długość fali świetlnej ( nr.1 )

3. Napięcie na anodzie fotokomórki nastawić na +20 V, a jej oświetlenie wyregulować przesłoną tak aby fotoprąd wskazywany przez mikroamperomierz wskazywał nieco mniej niż 4 μA (4000 jednostek ).

4. Wykonać pomiary fotoprądu zmieniając stopniowo napięcie aż do całkowitego jego zaniku .

5. Wykreślić charakterystykę prądowo napięciową fotokomórki.

6. Dla każdego filtru ustalić wartość napięcia hamującego, powodującego zanik fotoprądu. Odczytać wartość napięcia hamującego V_h . Pomiar powtórzyć trzy razy.

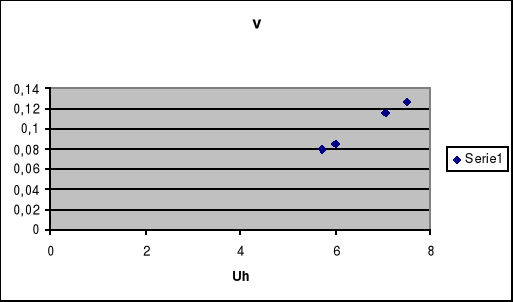
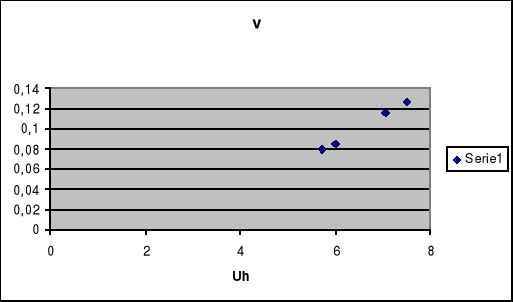
7. Sporządzić wykres zależności napięcia hamowania od częstotliwości.

8. Wyznaczyć z wykresu stałą Plancka i pracę wyjścia stosując regresje liniową.

Informacje dodatkowe:

Maksymalna przepuszczalność filtrów.

Nr filtru	1	2	3	4
λ [nm]	400	425	500	525

Analiza pomiarów:

U [V]	I [A]
19,95	0,243
19,55	0,23
19,02	0,236
18,45	0,224
17,96	0,213
17,45	0,219
16,91	0,214
14,91	0,198
14,44	0,207
13,85	0,197
13,29	0,187
12,55	0,195
11,94	0,193
11,22	0,181
10,85	0,179
10,54	0,182
9,99	0,185
9,48	0,176
8,95	0,179
8,66	0,18
8	0,164
7,45	0,156
7,02	0,151
6,53	0,143
6	0,14
5,44	0,133
4,97	0,126
4,53	0,116
3,99	0,108
3,56	0,103
3	0,092
2,51	0,073
1,93	0,057
1,4	0,039
0,98	0,025
0,55	0,009
0,01	-0,009
-0,45	-0,023
-1,02	-0,031
-1,61	-0,033
-2,04	-0,033

filtr	UH [V]	UH [V]	UH [V]	UH [V]	 [nm]	 [Hz]
1	0,133	0,126	0,126	0,126	400	7,5*10^14
2	0,113	0,116	0,089	0,116	425	7,06*10^14
3	0,086	0,087	0,086	0,085	500	6*10^14
4	0,079	0,082	0,079	0,08	525	5,72*10^14
	pomiar I	pomiar II	pomiar III	pomiar IV

Obliczenia:

,gdzie c - prędkość światła,  - długość fali świetlnej,  - częstotliwość fali świetlnej

Korzystając z regresji liniowej y=A+Bx możemy wyznaczyć tangens kąta nachylenia prostej, opisanej równaniem (3), czyli wartość , oraz punkt przecięcia prostej z osią rzędnych czyli wartość .

A= -1,607

B=3,752*10^-15

Rachunek błędu:

Wynik końcowy:

Wnioski:

Porównując otrzymaną w czasie doświadczenia wartość stałej Plancka x_p z wartością tablicową według kryterium zgodności widać, że otrzymana wartość mieści się w obliczonej granicy błędu.

U_o

Rys. 1 Energia potencjalna w krysztale

+

A

V

-

Rys.3 Układ do badania charakterystyki fotokomórki

Rys.2 Budowa

fotokomórki

6

3

4

5

8

1

2

7

---