Numer ćwiczenia: 6
|
Temat ćwiczenia: Mostek pojemnościowy |
Ocena z teorii: |
Numer zespołu 6
|
Nazwisko i imię: Marek Wiercioch
|
Ocena zaliczenia ćwiczenia: |
Data: 24.02.2004
|
Wydział: EAIiE Rok: I Grupa: 7 |
Uwagi:
|
Cel ćwiczenia:
Celem ćwiczenia jest zapoznanie się z metodą mostkową pomiaru nieznanej wartości pojemności kondensatora oraz połączeń szeregowych i równoległych kondensatorów.
Wprowadzenie teoretyczne:
Pojemność kondensatora
Zdolność gromadzenia przez ciało ładunku nazywamy pojemnością elektryczną danego ciała. Pojemnością kondensatora płaskiego C nazywamy stosunek ładunku q zgromadzonego na okładkach do napięcia U panującego na zaciskach:
![]()
[C] = c/V = A2s4/kgm2 = F (farad)
Pojemność kondensatora jest wprost proporcjonalna do powierzchni czynnej płytek. Natomiast odwrotnie proporcjonalna do odległości między tymi płytkami. Izolator znajdujący się między okładkami może zmieniać natężenie pola między nimi i tym samym powodować zmianę pojemności kondensatora. Korzystając z powyższych zależności możemy zapisać:
![]()
[C] = c2m/N m2 = c2/N m = A2s4/kg m2 = F (farad)
gdzie: Eo - przenikalność elektryczna próżni
Er - przenikalność elektryczna izolatora
s - powierzchnia czynna płytek
d - odległość między płytkami
Rodzaje połączeń kondensatorów (Cw - pojemność wypadkowa):
Szeregowe
C1 C2 Cn
![]()
Równoległe
C1
C2
Cw = C1+C2+...+Cn
Opór czynny i bierny
Opór elektryczny czynny (rezystancja) - oznaczamy R, jest to stosunek różnicy potencjałów na końcach elementu elektrycznego do natężenia prądu przepływającego przez niego. Jest to zatem miara oporu, jaki dany element stawia przepływowi ładunku elektrycznego.
Opór elektryczny bierny (reaktancja) - dla kondensatora oznaczamy Xc - jest to właściwość obwodu elektrycznego zawierającego pojemność elektryczną, która wraz z oporem czynnym tworzy opór elektryczny pozorny. Opór elektryczny pozorny Z jest dany wzorem Z2 = R2 + X2, gdzie R jest oporem czynnym danego obwodu. Dla czystej pojemności C opór elektryczny bierny jest dany przez: Xc = 1/(2fC
),
gdzie f jest częstością prądu zmiennego .
3. Zasada pomiaru za pomocą mostka Wheatstone'a / Przepływ prądu zmiennego przez kondensator
Mostek Wheatstone`a jest układem do pomiaru (porównywania) oporów. Tworzy go połączenie czterech oporów : Rx, R2, R3, R4 oraz galwanometru o oporze R5. Mostek jest zasilany z ogniwa galwanicznego lub zasilacza.
Jeśli dana jest siła elektromotoryczna oraz opory Rx, R2, R3, R4, R5, można znaleźć natężenia wszystkich prądów płynących w mostku. Metoda mostka Wheatstone`a polega na porównywaniu oporów na tzw. równoważeniu mostka, tzn. na takim dopasowaniu oporów, aby prąd I5 płynący przez galwanometr był równy zero. Aby eksperymentalnie wyznaczyć Rx korzystamy z wyrażenia :
.
Jeżeli do kondensatora przyłożymy napięcie sinusoidalnie zmienne:
U(t) = U0 cos (![]()
t)
to zgodnie z równaniem Q = CU ładunek kondensatora też zmienia się w czasie,
Q(t) = C U0 cos (![]()
t)
Zmiana ładunku kondensatora oznacza, że do jego okładek dopływa lub odpływa ładunek, czyli płynie prąd przemienny. Ponieważ I = dQ/dt, więc obliczając pochodną wyrażenia
Q(t) = C U0 cos (![]()
t)
otrzymujemy: I(t) = -![]()
CUosin(![]()
t)
Prąd chwilowy I(t) ma więc charakter sinusoidalny, podobnie jak napięcie U(t) na kondensatorze, lecz czasowo wyprzedza w fazie napięcie o kąt
/2. Maksymalna wartość prądu równa I0=![]()
CUo jest proporcjonalna do maksymalnego napięcia Uo.
Najprostszym typem mostka pojemnościowego jest mostek pokazany na załączonym rysunku. Służy on do pomiaru nieznanej pojemności CX na podstawie znanych wartości C oraz R1 i R2. Przy zastosowaniu metody symbolicznej wyprowadzenie warunku równowagi mostka pojemnościowego jest takie samo, jak w przypadku mostka oporowego.
Uzyskujemy : ![]()
Sposób wykonania ćwiczenia:
1. Zestawić obwód elektryczny według schematu pokazanego na rysunku, włączając
w obwód kondensator o nieznanej pojemności CX.
UWAGA: W miejsce regulowanych oporników R1 i R2 zastosowano potencjometr.
Wartość R1 odpowiada wskazaniu potencjometru d, natomiast R2 odpowiada
wartości d - 1000.
2. Włączyć oscyloskop oraz generator. Na ekranie widoczny będzie obraz przebiegu
sinusoidalnego.
3. Zrównoważyć mostek - doprowadzić do uzyskania możliwie najmniejszej amplitudy
przebiegu na ekranie oscyloskopu, w następujący sposób:
a) ustawić potencjometr w pobliżu 400 działek na skali,
b) na kondensatorze dekadowym tak dobrać wartość pojemności C, aby uzyskać
zgrubne zrównoważenie mostka - aby amplituda przebiegu obserwowanego na
ekranie była jak najmniejsza,
c) poprzez regulację potencjometrem zrównoważyć precyzyjnie mostek - amplituda
przebiegu powinna zmaleć do zera.
4. Odczytać i zanotować wartości C oraz d. Powtórzyć pomiary z punktów b) i c) dla
potencjometru ustawionego na 500 i 600 działkach.
5. Wyniki pomiarów i obliczeń zanotować w tabeli:
Oznaczenie badanego kondensatora |
C[µF] |
d |
Cx[µF] |
_ Cx[µF] |
ΔCx[µF] |
I.1μF K400V MKSE-012 |
1.210 |
440 |
0.951 |
0.976 |
0.007 |
|
0.991 |
500 |
0.991 |
|
|
|
0.657 |
600 |
0.986 |
|
|
II. MIFLEX 0,47μF J 250V
|
0.670 |
399 |
0.445 |
0.441 |
0,004 |
|
0.442 |
500 |
0.442 |
|
|
|
0.291 |
600 |
0.437 |
|
|
III. MIFLEX 47nF K 630V |
0.062 |
416 |
0.044 |
0.044 |
0,002 |
|
0.044 |
499 |
0.044 |
|
|
|
0.029 |
604 |
0.044 |
|
|
IV. MIFLEX 0,22μF K 250V |
0.315 |
400 |
0.210 |
0.208 |
0.003 |
|
0.208 |
500 |
0.208 |
|
|
|
0.130 |
613 |
0.206 |
|
|
Połączenie równoległe 0,22μF i 1μF |
1.217 |
495 |
1.193 |
1.193 |
0.008 |
|
0.998 |
545 |
1.195 |
|
|
|
0.780 |
604 |
1.190 |
|
|
Połączenie szeregowe 47nF i 0,47μF |
0.064 |
400 |
0.043 |
0.042 |
0,001 |
|
0.042 |
500 |
0.042 |
|
|
|
0.028 |
600 |
0.042 |
|
|
6. W analogiczny sposób zmierzyć pojemności pozostałych kondensatorów oraz
pojemności zastępcze różnych połączeń tych kondensatorów.
Opracowanie wyników
1. Wartość mierzonej pojemności Cx obliczam ze wzoru : ![]()
przykład: dla pierwszego pomiaru dla kondensatora: 1μF :
Cx=1,210 ![]()
=0,95071...![]()
0,951
2. Pojemności zastępcze obliczam z następujących zależności:
dla połączenia równoległego:
Cw = C1+C2 ,
Dla takiego połączenia kondensatorów 0,22μF i 1μF, otrzymujemy:
Cw = 1 + 0.22 = 1.22 [μF]
dla połączenia szeregowego :
![]()
,
Dla takiego połączenia kondensatorów 47nF i 0,47 μF, otrzymujemy:
Cw=![]()
stąd Cw![]()
0.042 [μF]
3. Niepewności pomiarowe uzyskanych wartości pojemności obliczam z prawa przenoszenia błędów:
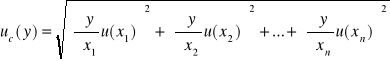
Cx (d, C), gdzie: Cx = C![]()
zakładam, że: Δd = 1, ΔC = 0.001
![]()
, ![]()
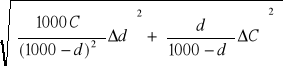
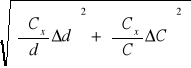
ΔCx = = =
Dla pierwszego kondensatora (1μF):
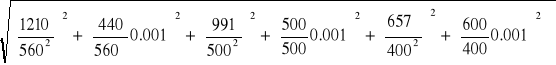
=
≈ 0.007,
Analogiczne obliczam dla pozostałych.
47μF :
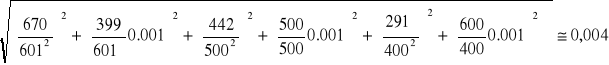
47nF:
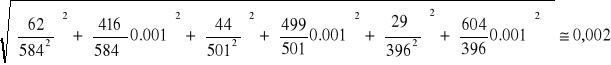
22μF:
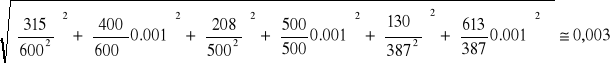
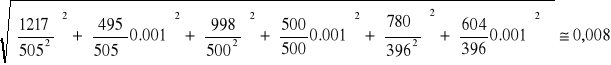
Połączenie równoległe 0,22μF i 1μF
Połączenie szeregowe 47nF i 0,47μF
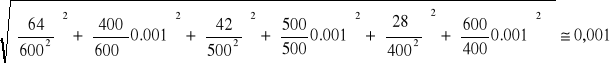
Wnioski i uwagi:
Po przeanalizowaniu otrzymanych przeze mnie wyników w doświadczeniu, stwierdziłem, że mogę zastosować zaokrąglenie wyników znajdujących się na pozycjach dalszych niż 3-e miejsce po przecinku, ponieważ nie mają one większego wpływu na otrzymane wyniki oraz nie wpływają drastycznie na obliczenia błędu.
Błąd wartości pojemności zastępczych obliczony z prawa przenoszenia błędów dla rożnych połączeń kondensatorów w porównaniu z wartościami zmierzonymi nie jest większy niż 3% co świadczy o wysokiej klasie dokładności urządzeń pomiarowych oraz staranności studentów wykonywujących dane ćwiczenie.
5
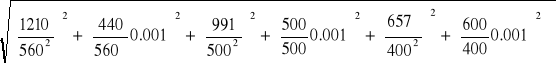
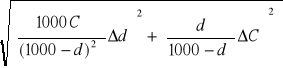
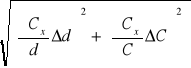
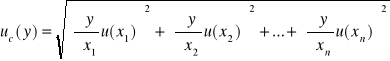
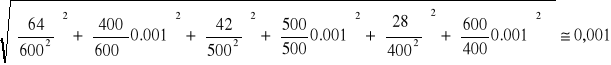
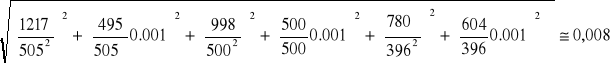
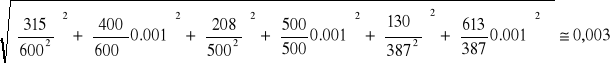
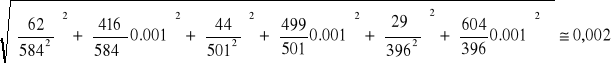
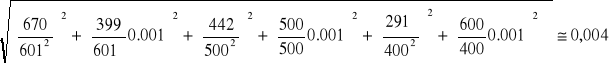
Wyszukiwarka
Podobne podstrony:
OGNIWA (2), Sprawozdania - Fizyka
Ćwiczenie nr 50b, sprawozdania, Fizyka - Labolatoria, Ćwiczenie nr50b
Mech- Badanie zależności współczynnika lepkości cieczy od te, Sprawozdania - Fizyka
Doświadczalne spr p. Malusa, sprawozdania, Fizyka - Labolatoria, Ćwiczenie nr70
Sprawozdanie Fizyka ćwiczenie 4(M04)
ćw13 sprawozdania fizyka 3, Sprawozdanie
3 W LEPKO CIECZY, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, labor
Pomiar promieni krzywizny soczewki płasko - wypukłej, Sprawozdania - Fizyka
Ćwiczenie nr 82, sprawozdania, Fizyka - Labolatoria, Ćwiczenie nr82
PUZON, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, Laborki s
Moment Bezwładności, Sprawozdania - Fizyka
Wyznaczanie momentu bezwładności brył za pomocą drgań skrę(1 (2), Sprawozdania - Fizyka
Ćwiczenie nr 65c, sprawozdania, Fizyka - Labolatoria, Ćwiczenie nr65c
test metale tabela, Studia, Ogólne, Fiyzka, od romka, fizyka, sprawozdania fizyka
Bezwladnosc tab, Sprawozdania - Fizyka
Mech- Wyznaczanie ciepła topnienia lodu(1), Sprawozdania - Fizyka
Atom- Wyznaczanie stałej Plancka i pracy wyjścia elektronów(1), Sprawozdania - Fizyka
Sprawozdanie Fizyka ćwiczenie 6(O01)
więcej podobnych podstron