UNIWERSYTET WARMIŃSKO -MAZURSKI

W OLSZTYNIE

KATEDRA FIZYKI

ĆWICZENIA LABORATORYJNE Z FIZYKI

Temat: Promieniowanie temperaturowe. Wyznaczanie rozkładu energetycznego ciała promieniującego w funkcji temperatury. Sprawdzenie prawa Wiena.

Promieniowanie temperaturowe jest najbardziej powszechną w przyrodzie formą promieniowania elektromagnetycznego. Jego emisja zachodzi kosztem energii ruchu cieplnego atomów oraz cząsteczek dowolnego ciała. Emitują je wszystkie ciała o dowolnej temperaturze, większej od zera bezwzględnego. Zakres widma promieniowania temperaturowego zawiera się w przedziale od podczerwieni do nadfioletu. Energia emitowana przez ciało jest zawsze równa sumie energii wyzwolonej w wyniku zmian jego energii wewnętrznej, niezależnie od sposobu, w jaki zostanie naruszony stan jego równowagi termodynamicznej.

Ilość energii wypromieniowanej z 1 m³ powierzchni ciała w ciągu 1 s w zakresie wszystkich długości fal nazywamy całkowitą emisją energetyczną lub całkowitą gęstością promieniowania.

Energia promieniowania, które pada na dane ciało E, może być przez nie pochłonięta E_a, odbita E_σ lub przepuszczona E_ρ.

E = E_a + E_σ + E_ρ

Współczynnik pochłaniania (zdolność absorpcyjna): a = Φ_a/Φ_o

Współczynnik odbicia: σ = Φ_σ/Φ_o

Współczynnik przepuszczalności: ρ = Φ_ρ/Φ_o

Współczynnik emisji (zdolność emisyjna): e = Φ_e/Φ_oc

gdzie:

Φ_a - strumień energetyczny pochłonięty przez ciało

Φ_σ - strumień energetyczny odbity przez ciało

Φ_ρ - strumień energetyczny, który przeszedł przez ciało

Φ_o - strumień energetyczny padający na ciało

Φ_e - strumień energii wypromieniowanej przez dane ciało

Φ_oc - strumień energii wypromieniowanej przez ciało dosk. czarne w tej samej temperaturze

Przez ciało doskonale czarne rozumie się takie ciało, które w każdej temperaturze T>0 pochłania wszelkie padające nań promieniowanie dowolnej długości fali.

Współczynniki pochłaniania, odbicia i przepuszczalności danego ciała zależą od długości fali padającego na nie promieniowania i od temperatury ciała. Zdolności emisyjne i absorpcyjne ciał są wzajemnie proporcjonalne.

Prawo Stefana - Boltzmanna:

Ilość energii E wypromieniowanej w jednostce czasu przez jednostkę powierzchni S ciała doskonale czarnego w całą półprzestrzeń (dla kąta bryłowego 2Π) w funkcji temperatury jest określona wyrażeniem:

E = δ T⁴

gdzie:

δ - stała Stefana - Boltzmanna = 5.75 ⋅ 10^-8 [W/m²K4]

Dla ciała rzeczywistego należy uwzględnić współczynnik emisji e tego ciała:

E = δ e T⁴

Prawo Kirchhoffa:

Dla promieniowania zrównoważonego stosunek zdolności emisyjnej ciała do jego zdolności absorpcyjnej równa się natężeniu promieniowania zrównoważonego ciała doskonale czarnego:

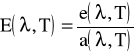
z tego wynika, że:

- zdolność emisyjna dowolnego ciała jest równa iloczynowi jego zdolności absorpcyjnej i zdolności emisyjnej ciała dosk. czarnego w tej samej temp.

- zdolność emisyjna dowolnego ciała jest mniejsza od zdolności emisyjnej ciała dosk. czarnego w tej samej temp.

- jeżeli ciało w jakiejś temp. emituje promieniowanie o określonej długości fali, to musi ono również pochłaniać promieniowanie o tej samej długości fali.

Prawo Wiena:

Długość fali λ₀, której odpowiada maximum zdolności emisyjnej ciała doskonale czarnego jest odwrotnie proporcjonalna do jego temperatury bezwzględnej:

λ₀ = b/T λ₀⋅T = b = const

gdzie:

b - stała Wiena = 0,0028978 mK

Ze wzrostem temperatury rośnie całkowita emisja energetyczna ciała doskonale czarnego i zmienia się widmowy rozkład energii.

Prawo Planck'a:

Energia elektromagnetyczna jest emitowana oraz rozprzestrzeniana tylko w postaci ściśle określonych, oddzielnych porcji energii E-kwantów. Ilości energii przenoszone przez fale elektromagnetyczne stanowią całkowite wielokrotności kwantu energii E, są więc równe nE (gdzie n = 1,2,3,...). Wzór Planck'a dający rozkład natężeń w widmie promieniowania:

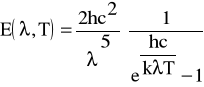
gdzie:

c - prędkość światła w próżni

k - stała Boltzmanna

Dyspersja liniowa i kątowa:

Rozczepienie światła w ośrodku wynika z tego, że współczynnik załamania promienia zależy od jego długości fali:

n = f(λ)

Dyspersję materiału D_m definiuje się jako stosunek zmiany współczynnika załamania n w odniesieniu do niewielkiej różnicy długości fali:

D_m = - dn/dλ

Ze wzrostem długości fali maleje wartość współczynnika załamania.

Dyspersja kątowa D_ϕ jest stosunkiem zmiany kąta Φ, pod jakim rozchodzą się po wyjściu z pryzmatu dwa promienie o blisko siebie leżących długościach fali λ, do różnicy ich długości dλ:

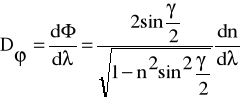
gdzie:

γ - kąt załamania pryzmatu

n - wsp. załamania pryzmatu

Dyspersja liniowa D_L jest miarą odległości dL obrazu dwóch promieni różniących się długością fali o dλ (określa ona szerokość otrzymanego obrazu widma):

D_L = dL/dλ

Krzywa dyspersji - przedstawia zależność współczynnika załamania od długości fali, otrzymujemy ją odkładając na osi odciętych długość fali, a na osi rzędnych współczynnik załamania.

	Dla 2,6 [A]	Dla 3,2 [A]	Dla 4 [A]
720	0,003	0,011	0,008
740	0,003	0,017	0,017
760	0,004	0,023	0,031
780	0,005	0,033	0,052
800	0,01	0,045	0,073
820	0,015	0,055	0,095
840	0,022	0,065	0,119
860	0,031	0,075	0,13
880	0,035	0,085	0,155
900	0,036	0,1	0,181
920	0,037	0,103	0,202
940	0,044	0,113	0,214
960	0,048	0,123	0,223
980	0,053	0,132	0,232
1000	0,054	0,14	0,24
1020	0,058	0,154	0,245
1040	0,063	0,156	0,254
1060	0,066	0,155	0,257
1080	0,068	0,158	0,252
1100	0,069	0,165	0,244
1120	0,071	0,168	0,235
1140	0,074	0,173	0,232
1160	0,075	0,177	0,237
1180	0,076	0,174	0,242
1200	0,08	0,163	0,247
1225	0,081	0,16	0,247
1250	0,079	0,16	0,245
1275	0,078	0,159	0,243
1300	0,075	0,158	0,238
1325	0,073	0,154	0,232
1350	0,072	0,149	0,223
1375	0,073	0,143	0,217
1400	0,073	0,139	0,211
1425	0,072	0,134	0,205
1450	0,07	0,129	0,194
1475	0,067	0,123	0,182
1500	0,059	0,114	0,164
1525	0,053	0,107	0,152
1550	0,051	0,103	0,139
1575	0,047	0,095	0,129
1600	0,044	0,089	0,122
1625	0,043	0,083	0,121
1650	0,043	0,08	0,119
1675	0,042	0,083	0,114
1700	0,04	0,08	0,122
1725	0,04	0,078	0,117
1750	0,041	0,073	0,109
1775	0,039	0,07	0,096
1800	0,035	0,066	0,087

δ_^ m]

δ_u=0,001 [v]

_max(2,6)=1225[nm]

_max(3.2)=1160[nm]

_max(4)=1080[nm]

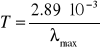
T₁=2359,18 ^oK

T₂=2491,37 ^oK

T₁=2726,41 ^oK

Błąd:

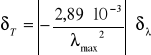
δ_ ^

δ_ ^

δ_ ^

Porównując włókno żarówki do ciała doskonale czarnego, wiemy iż wolfram ma najbardziej podobne widmo promieniowania temperaturowego do promieniowania tego ciała. Jednak wykresy otrzymane z przeprowadzonego doświadczenia różnia się od wykresu ciała doskonale czarnego. Przyczyna tej różnicy są urządzenia (monochromator, detektor) oraz będące składnikami żarówki (bańka szklana , gaz) , które to powodują zakłócenia mające wpływ na wynik końcowy.

---