SPRAWOZDANIE Z WYKONANIA ĆWICZENIA

Anna Kozdrańska 14 grudnia 2010

II rok, fizyka techniczna dr Jacek Brona

wtorek 16⁰⁰

Ćwiczenie 69: Badanie zjawiska fotoelektrycznego i wyznaczanie stałej Plancka.

Tabela wyników1

Stała Plancka
Praca wyjścia 1
Praca wyjścia 2:

Wstęp teoretyczny:

Zjawisko fotoemisji elektronów z metali:

Zjawisko fotoelektryczne w najogólniejszym ujęciu polega na wyzwalaniu elektronów w materii pod wpływem energii fotonów promieniowania. Opierając się na pojęciu kwantowej natury światła, Einstein (1905r.) zastosował do zjawiska fotoelektrycznego prawo zachowania energii i podał ilościową zależność między energią kwantów padającego promieniowania wywołującego fotoefekt i energią, jaką otrzymuje wyzwolony elektron. Energia pojedynczego kwantu promieniowania wynosi:

gdzie  jest częstością drgań, λ długością fali padającego promieniowania, h - uniwersalną stałą Planca wynoszącą h=6,62*10^-34.

Fotokomórka próżniowa:

Fotokomórka próżniowa została wynaleziona w 1895 przez fizyków niemieckich Hansa Geitela i Juliusa Elstera. Odkryli oni, że promienie katodowe mogą być emitowane z katody po oświetleniu jej dowolnym światłem, a natężenie tych promieni jest wprost proporcjonalne do natężenia padającego światła. Podstawowym elementem współczesnej komórki fotoelektrycznej jest warstwa metaliczna napylona na wewnętrznej ściance szklanej bańki. Wewnątrz bańki znajduję się spiralna elektroda metalowa. Elektrodę tę łączy się z dodatnim biegunem baterii, dlatego nazwana została anodą. Rolę katody spełnia światłoczuła warstwa metaliczna, która łączy się z ujemnym biegunem baterii.

Wyjaśnienie mechanizmu zjawiska fotoelektrycznego wg Einsteina:

Einstein oparł się na śmiałym załorzeniu, że światło wysyłane jest i rozchodzi się w przestrzeń pewnymi porcjami o określonej energii. Te porcje promieniowania nazwano kwantami, jednakże nie wszystkie kwanty promieniowania posiadają jednakową energię. Przyjęcie hipotezy o nieciągłej budowie światła nie uczyniło bezużyteczną teorię falową. Energia bowiem kwantu zależy od częstotliwości drgań, z którą wiąże się długość fali światła. Podana przez Plancka zależność wskazuje, że energia kwantu E jest wprost proporcjonalna do częstotliwości ν:

gdzie h jest współczynnikiem proporcjonalności. Współczynnik ten jest stałą fizyczną nazwaną od nazwiska twórcy tej teorii- stałą Plancka i wynosi ona

Pędzący kwant światła posiada pewną energię, której wartość hν zależy od długości fali świetlnej. Jeżeli energia kwantu jest dość duża, zderzenie jego z powierzchnią metalu spowoduję wybicie elektronu z atomu. Wybicie bowiem elektronu wiąże się z wykonaniem pracy „wyrzucenia” elektronu z atomu i udzielenie mu pewnej energii kinetycznej, a praca ta wykonuję się kosztem energii światła, padającego na powierzchnię metalu. Elektron pochłaniając kwant , część pochłanianej energii zużywa na wykonanie pracy wyjścia W, a pozostałą zachowuje w postaci energii kinetycznej, wiec:

Ponieważ energia „wyrzucenia” elektronu z atomu jest mała w porównaniu z energią kinetyczną wybitego elektronu, w przybliżeniu możemy zapisać”

gdzie m oznacza masę elektronu, v- prędkość jaką uzyskał opuszczając powierzchnię metalu.

Prawa fotoelektryczne:

I prawo fotoelektryczne:

Ilość fotoelektronów emitowanych z katody w jednostce czasu dlatego zależy od odległości fotokomórki od światła, ponieważ im ta odległość jest mniejsza, tym więcej kwantów światła pada w jednostce czasu na powierzchnię metalu. Każdy zaś kwant może wybić jeden fotoelektron.

II prawo fotoelektryczne:

Prędkość, z jaką elektron opuszcza katodę, nie może zależeć od odległości między fotokomórką, a źródłem światła, ponieważ zmiana tej odległości nie powoduję zmiany energii, z jaką kwant oddziałuję na fotoelektron. Prędkość swą fotoelektron uzyskać może jedynie pod wpływem energii z jaką oddziałuję nań kwant światła.

III prawo fotoelektryczne:

Energii emitowanemu fotoelektronowi udziela kwant światła. Ponieważ zaś energia kwantu zależy od długości fali światła, więc od tej wielkości zależeć musi energia fotoelektronu.

Opis metody wyznaczania stałej Plancka i pracy wyjścia:

Prąd fotoelektryczny płynie nawet wtedy, gdy między anodą i katodą nie ma napięcia. Dzieje się tak dzięki energii kinetycznej posiadanej przez elektrony w momencie wybicia z metalu. Całkowity zanik prądu można spowodować przykładając napięcie o przeciwnej polaryzacji, tzn. potencjał niższy na anodę. Jeżeli napięcie ma odpowiednią wartość zwaną potencjałem hamującym V_h to następuje całkowite zahamowanie elektronów - ich energia kinetyczna zostaje zużyta na wykonanie pracy przeciwko polu elektrycznemu.

Uwzględniając powyższy związek możemy przekształcić równanie do postaci :

Na podstawie wykresu zależności V_h=f(υ) można znaleźć stałą Plancka h oraz pracę wyjścia W, gdyż tangens kąta nachylenia prostej opisanej równaniem wynosi h/e, a punkt przecięcia prostej z osią rzędnych ma wartość - W/e.

Przebieg doświadczenia:

Na początku należało podłączyć obwód według schematu:

A następnie wykonałyśmy pomiary natężenia prądu dla 6 diod.

Tabele pomiarowe:

Tabela pomiarowa 1:

U[V]	P1 I [μA]	P2 I [μA]	P3 I [μA]	P4 I [μA]	P5 I [μA]	P6 I [μA]
0	1,9	2,9	1,8	0,5	0,3	0,1
0,005	1,8	2,6	1,5	0,4	0,2	0
0,01	1,6	2,4	1,3	0,3	0,1	0
0,015	1,4	2,1	1,1	0,2	0,1	0
0,02	1,2	1,8	0,9	0,1	0	0
0,025	1,1	1,5	0,7	0,1	0	0
0,03	0,9	1,3	0,5	0	0	0
0,035	0,7	1,0	0,3	0	0	0
0,04	0,6	0,8	0,2	0	0	0
0,045	0,5	0,6	0,1	0	0	0
0,05	0,4	0,5	0,1	0	0	0
0,055	0,3	0,3	0	0	0	0
0,06	0,2	0,2	0	0	0	0
0,065	0,1	0,1	0	0	0	0
0,07	0,1	0	0	0	0	0
0,075	0	0	0	0	0	0

Tabela pomiarowa 2:

Kolor	Niebieska I	Niebieska II	Zielona	Żółta	Pomarańcz.
[nm]	430	470	502	575	621
[×10^14Hz]	6,98	6.38	5,98	5,22	4,83

Wykresy:

Wykres zależności natężenia fotoprądu od napięcia hamującego:

W programie Microsoft Excel zostały obliczone równania funkcji zależności natężenia fotoprądu od napięcia hamującego:

Dioda niebieska I : y = 211,48x² - 42,038x + 1,9667

Dioda niebieska II: y = 374,65x²-68,54x+2,9756

Dioda zielona: y = 441,88x² - 57,053x + 1,8146

Dioda żółta: y = 182,07x² - 19,244x + 0,4689

Dioda pomarańczowa: y = 108,54x² - 10,817x + 0,2391

Dioda 6: y = 24,51x² - 2,2794x + 0,0442

Wykres zależności napięcia odcięcia od częstotliwości drgań:

Opracowanie wyników:

Podane wyżej równania umożliwiły w prosty sposób na obliczenie napięć odcięcia dla poszczególnych diod. Wyniki zamieściłam w tabeli:

	UH [V]
Dioda niebieska I	0,075
Dioda niebieska II	0,069
Dioda zielona	0,057
Dioda żółta	0,038
Dioda pomarańczowa	0,033
Dioda 6	0,028

Współczynnik kierunkowy prostej regresji wykresu zależności napięcia odcięcia od częstotliwości drgań jest równy h/e ( w jednostkach Vs ) co pozwoli nam obliczyć stałą Plancka:

Parametr b w równaniu prostej regresji wykresu zależności napięcia odcięcia od częstotliwości drgań jest w prosty sposób związany z pracą wyjścia W elektronu z metalu: b=W/e w ten sposób została obliczona praca wyjścia:

W przeliczeniu na eV:

Obliczając pracę wyjścia używając częstości granicznej, otrzymujemy:

Widać, że paca obliczona pierwszym sposobem jest dwa razy mniejsza od tej obliczonej drugim sposobem. Wnioskujemy, że miała na to wpływ większa niepewność pomiarowa związana z dwoma współczynnikami prostej regresji.

Niepewności pomiarowe:

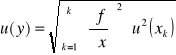
Stała Plancka:

Praca wyjścia:

Metoda pierwsza:

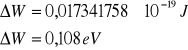
Metoda druga:

Wnioski:

Wartość stałej Plancka wyznaczonej w ćwiczeniu znacznie różni się od tej tablicowej, a także nie mieści się w przedziale błędu pomiarowego. Uważam, że rozbieżność ta nie jest jednak związana z niedokładnością przyrządów, ale wynika z błędu systematycznego układu pomiarowego. Natomiast wyznaczona praca wyjścia ma wartość nietypową dla metali pokrytych warstwą aktywacyjną, a w dodatku obliczona w dwa różne sposoby ma dwie różne wartości. Różnica ta jest 100%. Może być to spowodowane większą niepewnością pomiarową w drugim przypadku, a jej nietypowa wartość pewnie też jest związana z błędem systematycznym całego układu. Wydaje nam się, że na wyniki miała wpływ „tajemnicza czarna skrzynka”, która wraz z opornikami została włączona do obwodu, przez co obwód różnił się od tego w instrukcji. Oporniki mogły mieć znaczący wpływ na pomiar napięcia i natężenia, co wpłynęło na obliczenia.

1

---