Nr. ćwiczenia: 12 |
Temat: Wyznaczanie przerwy energetycznej.
|
Ocena z teorii: |
Zespół nr 9 |
Nazwisko i imię: Targosz Mateusz
|
Ocena zaliczenia ćwiczenia:
|
23.03.2004r. |
EAIiE, rok 1 EiT, grupa VII |
Uwagi:
|
W ciałach stałych energie elektronów ograniczone są do pewnych poziomów, które z kolei należą do pewnych pasm. Między poszczególnymi pasmami występują tzw. przerwy energetyczne. Przebywanie elektronu w takiej przerwie jest niemożliwe. Pasma wypełnione elektronami walencyjnymi noszą nazwę pasm walencyjnych (lub podstawowych), a pasma wypełnione częściowo lub puste (odpowiadające większym energiom) - pasm przewodnictwa. Elektrony znajdujące się w pasmach całkowicie zapełnionych nie wnoszą żadnego wkładu w przewodnictwo elektryczne, ze względu na brak wolnych, dozwolonych stanów energetycznych. W pasmach przewodnictwa (częściowo zapełnione lub puste) istnieją dozwolone puste stany energetyczne i elektrony pod wpływem np. zewnętrznego pola elektrycznego mogą przenosić się na nie, zatem biorą udział w przewodnictwie elektrycznym. Przewodniki są materiałami o niecałkowicie obsadzonym paśmie podstawowym lub o zlewających się ze sobą pasmach: podstawowym i przewodzenia. Jeżeli najwyższe zapełnione pasmo walencyjne jest oddzielone przerwą od najniższego pasma przewodnictwa to mamy do czynienia z półprzewodnikiem (przerwa energetyczna Eg<2 eV - elektrony mogą łatwo „przeskoczyć" przerwę energetyczną np. czerpiąc energię z fluktuacji termicznych) lub izolatorem (przerwa energetyczna Eg>2eV). Przerwę energetyczną Eg można wyznaczyć na kilka sposobów:
1.z zależności przewodnictwa elektrycznego od temperatury
2.z zależności przewodnictwa elektrycznego od energii padającego promieniowania
elektromagnetycznego
3.z pomiarów współczynnika absorbcji promieniowania elektromagnetycznego w
zależności od energii tego promieniowania.
Elektron może zwiększyć swoją energię jedynie kosztem absorpcji promieniowania elektromagnetycznego. Jeżeli na półprzewodnik padają fotony o energii wystarczającej na przeniesienie elektronu z pasma walencyjnego do pasma przewodnictwa to są one silnie absorbowane. Zatem w widmie absorpcyjnym półprzewodnika można wyróżnić gwałtowny wzrost współczynnika absorpcji w pobliżu energii hn równej szerokości przerwy energetycznej Eg. Efekty tego oddziaływania można prześledzić stosując tzw. materiałowe równania Maxwell'a. Rozwiązaniem tych równań jest równanie fali rozchodzącej się w ośrodku absorbującym:
![]()
gdzie n jest rzeczywistym współczynnikiem załamania, a wielkość ℵ jest to współczynnik ekstyncji, który opisuje absorpcję światła. Drugi czynnik ekspotencjalny opisuje tłumienie fali wraz z odległością. Natężenie fali jest wprost proporcjonalne do średniej czasowej z kwadratu pola elektrycznego (I ~ E2). Zatem stosunek natężenia promieniowania padającego do promieniowania, które przebyło pewną drogę wyraża się:
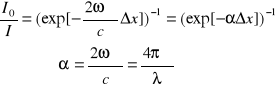
gdzie ![]()
to współczynnik absorpcji.
Definicją jego jest:
dI=- ![]()
I dx
gdzie dI to zmiana natężenia fali na odległości dx.
Przejścia elektronowe dla których elektron prawie nie zmienia swojego pseudo-pędu nazywamy przejściami prostymi. Występują one wtedy gdy: pj - pi = pp
gdzie pj - pseudo-pęd elektronu w stanie początkowym, pi - w stanie końcowym, a pp - pęd fotonu.
Ponieważ p=k oraz kp << ki,kj, to kj=ki, gdzie kj, ki są to odpowiednio wektor falowy elektronu w stanie początkowym i końcowym.
Wyrażenie na energetyczną zależność współczynnika absorbcji dla przejść optycznych w obszarze krawędzi absorbcji dane jest:
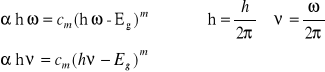
[25]
gdzie:
m= 1/2 dla przejść prostych dozwolonych
m= 3/2 dla przejść prostych wzbronionych
m= 2 dla przejść skośnych dozwolonych
m= 3 dla przejść skośnych wzbronionych
cm - stała zależna od rodzaju przejścia
Chcąc określić wartość przerwy energetycznej Eg z pomiarów optycznych należy wyznaczyć wartość współczynnika absorpcji , który z kolei można wyznaczyć z pomiarów współczynnika transmisji T, który jest stosunkiem natężenia fali elektromagnetycznej przechodzącej przez próbkę do natężenia fali padającej na próbkę. Transmisję światła można przedstawić jako:
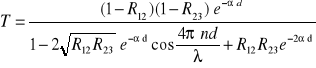
[26]
gdzie ![]()
jest współczynnikiem odbicia światła na granicy powietrze-warstwa, a ![]()
jest współczynnikiem odbicia światła na granicy warstwa-podłoże, ns jest współczynnikiem załamania podłoża, d grubość warstwy. Złożoność wyrażenia na transmisje wynika z faktu, iż światło przechodzące przez cienką warstwę ulega nie tylko absorpcji ale także wielokrotnym odbiciom na powierzchniach rozdzielających różne ośrodki optyczne. Ponad to w widmie transmisji występują maksima i minima interferencyjne. Zjawisko interferencji zachodzi ponieważ grubość warstwy półprzewodnika jest porównywalna z długością fali promieniowania elektromagnetycznego padającego na badaną próbkę.
Współczynnik załamania n można wyznaczyć korzystając z minimów i maksimów interferencyjnych transmisji z wzoru [26] podstawiając za cos() odpowiednio jego wartość maksymalną i minimalną. Z powstałych równań otrzymujemy:
![]()
[27]
gdzie:
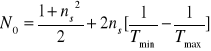
Mając wyznaczone R12 i R23 (niezależne od energii) oraz zmierzoną wartość transmisji T=T(hν), można wyliczyć dla każdej energii (długości fali) wartość współczynnika absorpcji korzystając ze wzoru:
![]()
[29]
Wzór ten jest słuszny w obszarze dużej absorpcji.
Wartość przerwy energetycznej należy policzyć korzystając z [25].
Opracowanie wyników
|
|
|
|
|
|
|
|
|
380 |
3 |
3,262105263 |
455 |
52 |
2,7243956 |
581 |
79 |
2,13356282 |
381 |
3 |
3,253543307 |
460 |
56 |
2,69478261 |
587 |
74 |
2,11175468 |
382 |
3 |
3,245026178 |
465 |
59 |
2,66580645 |
593 |
76 |
2,09038786 |
383 |
3 |
3,236553525 |
470 |
61 |
2,63744681 |
599 |
76 |
2,06944908 |
384 |
3 |
3,228125 |
475 |
64 |
2,60968421 |
605 |
77 |
2,04892562 |
385 |
4 |
3,21974026 |
480 |
67 |
2,5825 |
611 |
78 |
2,02880524 |
386 |
4 |
3,211398964 |
485 |
69 |
2,55587629 |
617 |
80 |
2,00907618 |
397 |
4 |
3,203100775 |
490 |
71 |
2,52979592 |
623 |
78 |
1,98972713 |
388 |
4 |
3,194845361 |
495 |
71 |
2,50424242 |
629 |
78 |
1,97074722 |
389 |
4 |
3,186632391 |
500 |
71 |
2,4792 |
635 |
75 |
1,95212598 |
390 |
4 |
3,178461538 |
503 |
75 |
2,46441352 |
641 |
75 |
1,93385335 |
395 |
5 |
3,138227848 |
509 |
72 |
2,43536346 |
647 |
75 |
1,91591963 |
400 |
6 |
3,099 |
515 |
74 |
2,40699029 |
653 |
76 |
1,89831547 |
405 |
9 |
3,060740741 |
521 |
76 |
2,37927063 |
659 |
79 |
1,88103187 |
410 |
11 |
3,023414634 |
527 |
77 |
2,35218216 |
665 |
82 |
1,86406015 |
415 |
15 |
2,986987952 |
533 |
75 |
2,32570356 |
671 |
81 |
1,84739195 |
420 |
19 |
2,951428571 |
539 |
76 |
2,29981447 |
677 |
80 |
1,8310192 |
425 |
23 |
2,916705882 |
545 |
76 |
2,27449541 |
683 |
83 |
1,81493411 |
430 |
28 |
2,882790698 |
551 |
77 |
2,24972777 |
689 |
82 |
1,79912917 |
435 |
34 |
2,849655172 |
557 |
78 |
2,22549372 |
695 |
80 |
1,78359712 |
440 |
38 |
2,817272727 |
563 |
79 |
2,2017762 |
701 |
79 |
1,76833096 |
445 |
43 |
2,785617978 |
569 |
78 |
2,17855888 |
|
|
|
450 |
48 |
2,754666667 |
575 |
76 |
2,15582609 |
|
|
|
W obszarze słabej absorpcji w wykresie T(λ) pojawiają się oscylacje. Znajdujemy najmniejszy i największy współczynnik T w tym obszarze:
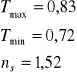
Po wstawieniu powyższych danych do wzoru, można wyliczyć współczynniki N0 oraz n.
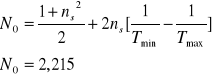
![]()
![]()
Długości fali przy których wykres T osiąga dwa kolejne minima wynoszą 533 nm i 587 nm. Na ich podstawie wyliczyć można grubość warstwy półprzewodnika:
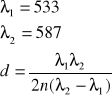
![]()
W obszarze silnej absorpcji możemy wyliczyć R12 i R23, korzystając z poniższych zależności:
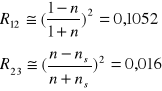
Na wykresach ![]()
dla kolejnych możliwych wartości n dopasowujemy wyniki doświadczalne do prostej aproksymującej. W celu wyliczenia Eg wystarczy teraz znaleźć punkt przecięcia prostej z osią E:
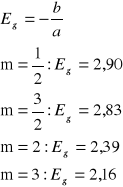
Ponieważ ostatnie wartości znajdują się w obszarze niskiej absorbcji, przyjmujemy wynik dla m równego ½.
![]()
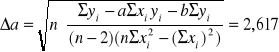
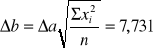
Korzystając z prawa przenoszenia błędu:
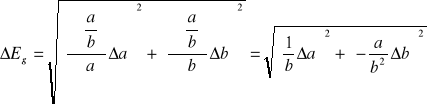
![]()
Wyszukiwarka
Podobne podstrony:
labolatorium2, agh wimir, fizyka, Fizyka(1)
10 moj konspekt, agh wimir, fizyka, Fizyka(1)
konspekt(1), agh wimir, fizyka, Fizyka(1)
samoindukcja cewki, agh wimir, fizyka, Fizyka(1)
Kospekt teoria, agh wimir, fizyka, Fizyka(1)
labolatorium4, agh wimir, fizyka, Fizyka(1)
tabele9, agh wimir, fizyka, Fizyka(1)
22wstep, agh wimir, fizyka, Fizyka(1)
Opracowanie 10, agh wimir, fizyka, Fizyka(1)
fizyka 2, agh wimir, fizyka, Fizyka
22opr, agh wimir, fizyka, Fizyka(1)
ZESTAW2A, agh wimir, fizyka, fiza
7 konspekt, agh wimir, fizyka, Fizyka(1)
konspekt Cw5, agh wimir, fizyka, Fizyka(1)
lab22wyniki, agh wimir, fizyka, Fizyka(1)
Mikrofale do druku, agh wimir, fizyka, Fizyka(1)
więcej podobnych podstron