1. Wstęp teoretyczny:

Interferencja światła.

Przy interferencji światła zachodzącej dzięki wielokrotnemu odbiciu w płytce płasko-równoległej otrzymane prążki nazwa się prążkami (interferencyjnymi) równego nachylenia, przy interferencji otrzymanej dzięki odbiciom w płytce o innych kształtach otrzymuje się tak zwane prążki równej grubości. W przypadku odbicia światła od cienkiej, płaskiej i przezroczystej warstwy naniesionej na inną substancję (np. nafty na wodzie) obserwuje się interferencję światła odbitego od powierzchni ze światłem od powierzchni granicznej rozdzielającej naftę i wodę. W przypadku oświetlenia światłem białym obserwuje się wygaszenie pewnych, oaz wzmocnienie innych baw, co obserwuje się jako mieniące się, tęczowe plamy barwne na wodzie. Zjawisko to nosi nazwę interferencji na cienkich warstwach.

Interferencję fal świetlnych szeroko wykorzystuje się głównie w badaniach podstawowych i stosowanych (interferometry optyczne, holografia i interferometria holograficzna).

Interferencja światła powstaje w wyniku nałożenia się na siebie fal świetlnych. Obserwujemy wtedy ich wzmocnienie lub wygaszenie w ściśle określonych punktach. Wzmocnienie następuje wtedy, gdy różnica ich dróg optycznych jest równa wielokrotności długości fali. Natomiast wygaszenie fali świetlnej obserwujemy wtedy, gdy różnica ich dróg optycznych jest wielokrotnością połówek długości fali.

Dyfrakcja i zasada Huyghensa.

Zjawisko dyfrakcji światła polega na uginaniu się promieni świetlnych napotykających na swej drodze przeszkody w wyniku, czego występują odstępstwa od prostoliniowego ich biegu, jest ściśle związane z falową naturą światła. Zjawisko to tłumaczy zasada Huyghensa mówiąca, iż każdy element powierzchni, do której dotarła fala, staje się źródłem nowej fali kulistej o częstości równej częstości fali padającej. Suma nowo powstałych fal przedstawia dalszą propagację fali, przy czym nie uwzględnia się obwiedni wstecznej.

Warunek wzmocnienia promieni ugiętych na siatce dyfrakcyjnej.

Siatką dyfrakcyjną nazywamy zbiór dużej liczby jednakowych, równoległych szczelin, między którymi występują równe odstępy. Warunek wzmocnienia możemy obserwować wówczas, gdy prowadzimy obserwację na wprost, wtedy fale wszystkich szczelin dodają się, ale również wtedy, gdy promienie wychodzące ze wszystkich szczelin pod kątem
, spełniają warunek

m=0,1,2,3... (maksima główne)

Gdzie m nazywamy rzędem widma.

Rodzaje widm. Analiza widmowa.

Widmo jest to rozkład natężenia promieniowania w zależności od jego energii, częstotliwości lub długości fali. Wyróżnia się widma: akustyczne, świetlne, radiowe, mikrofalowe, podczerwone, ultrafioletowe, rentgenowskie, promieniowanie gamma, alfa i beta, itp. Widmo dostarcza wielu informacji o źródle danego promieniowania (tzw. widmo emisyjne), a często i o ośrodku, przez który ono przenikało (tzw. widmo absorpcyjne).

Badanie widm różnego rodzaju nosi nazwę spektroskopii (lub spektrometrii).

2. Wykonanie ćwiczenia i odliczenia:

Stała siatki dyfrakcyjnej:

Ustawiłem płaszczyznę siatki dyfrakcyjnej równolegle do ekranu, a następnie włączyłem lampę sodową i wyznaczyłem na ekranie położenie 3 prążków.

Następnie zmierzyłem odległość pomiędzy siatką i ekranem, która była równa b = 0,637 [ m ]. Znając długość fali światła sodowego
[ nm ] obliczyłem wartość stałej siatki dla poszczególnych rzędów widma. Skorzystałem przy tym ze wzoru:

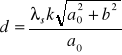
gdzie:

k - rząd widma

a₀ - średnia odległość prążka od szczeliny

Przykładowe obliczenia dla rzędu 1:

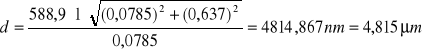
Następnie obliczyłem średnią arytmetyczną siatki dyfrakcyjnej:

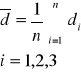
Wszystkie pozostałe obliczenia zamieściłem w poniższej tabeli pomiarowej nr 1.

Tabela pomiarowa nr 1:

Lampa	Kolor	k	a1 [ m ]	a2 [ m ]	a0 [ m ]	b [ m ]	λ [ nm ]	ds [ nm ]
Sodowa	Żółty	1	0,079	0,078	0,0785	0,637	588,9	4814,867
				2	0,159			0,158	0,1585			4877,824
				3	0,251			0,25	0,2505			4827,461
							średnia	4840,051

Długość fali świetlnej:

Nie zmieniając ustawienia siatki i ekranu włączyłem lampę mikroskopową i ustawiałem na kierunku biegu promieni różne filtry. Następnie wyznaczyłem położenie prążków dyfrakcyjnych 1 i 2 rzędu dla fal przepuszczonych przez poszczególne filtry.

Wszystkie pomiary znajdują się w poniższej tabeli nr 2:

Tabela pomiarowa nr 2:

Lampa	Kolor	k	a1 [ m ]	a2 [ m ]	a0 [ m ]	b [ m ]
Mikroskopowa	Żółty	1	0,072	0,069	0,0705	0,637
				2	0,143		0,143	0,143
			Czerwony	1	0,086		0,084	0,085	0,637
				2	0,173		0,173	0,173
			Niebieski	1	0,059		0,058	0,0585	0,637
				2	0,117		0,116	0,1165
			Pomarańczowy	1	0,08		0,079	0,0795	0,637
				2	0,159		0,158	0,1585

Następnie ze wzoru:

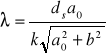
Obliczyłem długość fal świetlnych odpowiadających maksimum przepuszczalności filtrów.

Przykładowe obliczenia dla filtru żółtego, prążka 1:

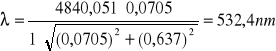
Wszystkie pozostałe obliczenia zamieściłem w poniższej tabeli pomiarowej nr 3.

Tabela pomiarowa nr 3:

Lampa	Kolor	k	a1 [ m ]	a2 [ m ]	a0 [ m ]	b [ m ]	ds [ nm ]	λ [ nm ]
Mikroskopowa	Żółty	1	0,072	0,069	0,0705	0,637	4840,051	532,4
				2	0,143			0,143	0,143			530,1
			Czerwony	1	0,086			0,084	0,085	0,637		640,2
				2	0,173			0,173	0,173			634,3
			Niebieski	1	0,059			0,058	0,0585	0,637		442,6
				2	0,117			0,116	0,1165			435,4
			Pomarańczowy	1	0,08			0,079	0,0795	0,637		599,4
				2	0,159			0,158	0,1585			584,3

3. Rachunek błędów:

Na podstawie przenoszenia niepewności pomiarowych, obliczyłem niepewności całkowite dla:

• długości fali świetlnej

Początkowo obliczam różniczki cząstkowe:

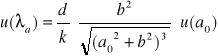
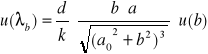
czyli:

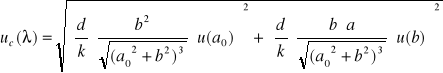
gdzie:

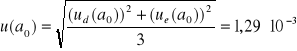
oraz

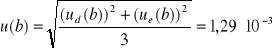
Podstawiając wszystkie dane do powyższego wzoru na błąd długości fali otrzymamy:

Lampa	Kolor	λ [ nm ]	uc(λ)
Mikroskopowa	Żółty	532,4219	± 1,29
				530,0783	±0,645
			Czerwony	640,1724	±1,29
				634,2686	±0,645
			Niebieski	442,6318	±1,29
				435,3736	±0,645
			Pomarańczowy	599,4064	±1,29
				584,3396	±0,645

4. Dyskusja wyników:

Celem mojego ćwiczenia było wyznaczenie długości fali świetlnej oraz stałej siatki za pomocą siatki dyfrakcyjnej.

Średnia wartość stałej siatki wynosi d_śr =4 840,051 [nm], natomiast długości fali lampy mikroskopowej i różnych filtrów zestawione są w tabeli nr 4.

W niektórych przypadkach jak widzimy długości fal dla rzędu pierwszego i drugiego nie pokrywają się z wartościami tablicowymi. Myślę, że różnica ta spowodowana jest tym, że lampy sodowe wewnątrz bańki szklanej nie posiadają wyłącznie sodu, ale znajduje się tam niewielka domieszka jakiegoś innego gazu, który również emituje falę cząstkową o pewnej długości.

W myśl zasady Huyghensa głoszącej, że wypadkowe zaburzenie rozchodzące się w ośrodku jest sumą wszystkich fal cząstkowych można przyjąć, że różnica wartości doświadczalnych i tablicowych jest właśnie tym spowodowana. Inną przyczyną rozbieżności wyników może być błąd pomiaru odległości L pomiędzy ekranem a siatką dyfrakcyjną lub fakt, że ekran i siatka dyfrakcyjna nie były ustawione równolegle względem siebie oraz, że w pomieszczeniu doświadczalnym nie panowała idealna ciemność.

---