ICHiP I rok	Palowski Artur	23.03.2010
Nr 23	Sprawdzanie prawa Malusa

Uwagi:

Wprowadzenie.

Fale świetlne - to fale elektromagnetyczne, związane z rozchodzeniem się w przestrzeni okresowo zmiennych pól: elektrycznego o natężeniu E i magnetycznego o natężeniu H. Ugięcie i interferencja światła są zjawiskami świadczącymi o jego naturze falowej. Ponieważ zjawiska te charakterystyczne są zarówno dla fal podłużnych jak i dla fal poprzecznych, nie pozwalają wyciągnąć wniosków co do charakteru fali. Do rozważań na temat charakteru fali świetlnej oprócz wektorów podstawowych wprowadza się tzw. wektor kierunkowy (np. jednostkowy), którego kierunek jest zgodny z kierunkiem rozchodzenia się promienia świetlnego. Badanie kierunków tych wektorów wykazały że w przestrzeni są one prostopadłe. Właśnie na tej wzajemnej prostopadłości wektorów polega poprzeczność fali świetlnej

Doświadczalnym dowodem poprzecznego charakteru fali świetlnej jest zjawisko polaryzacji.

Biorąc pod uwagę światło rozchodzące się bezpośrednio od źródła (tzw. światło naturalne), należy pamiętać o tym, że choćby źródło miało najmniejsze rozmiary ,jest w nim bardzo dużo atomów odpowiedzialnych za wysyłanie fal elektromagnetycznych. Dzięki tej mnogości atomowych źródeł występują zmiany wektora świetlnego we wszystkich kierunkach prostopadłych do wektora . Takie promieniowanie nazywamy niespolaryzowanym.

Jeżeli zmiany wektora E we wszystkich falach składowych potrafimy sprowadzić do jednej płaszczyzny, zawierającej wektor v mamy do czynienia ze światłem liniowo spolaryzowanym.

Płaszczyzna przechodząca przez wypadkowy wektor E i v nosi nazwę płaszczyzny drgań wektora świetlnego, ponieważ wektor ten wywołuje wrażenie świetlne. Płaszczyznę do niej prostopadłą (zawierającą wektor H i v) nazywamy według umowy przyjętej w optyce - płaszczyzną polaryzacji.

Przyrządy służące do przekształcania światła naturalnego (lub częściowo spolaryzowanego) w światło spolaryzowane liniowo nazwane zostały polaryzatorami.

Działanie ich oparte jest na wykorzystaniu albo odbicia światła na granicy rozdziału dwóch przeźroczystych i izotropowych dielektryków, albo zjawiska podwójnego załamania w kryształach jednoosiowych. Przykładem polaryzatora pierwszego rodzaju może być płasko równoległa płytka szklana.

Brewster wykazał, że jeśli promień odbity i załamany tworzą kąt prosty, to promień odbity jest całkowicie liniowo spolaryzowany. Zgodnie z prawem Brewstera, światło odbite jest spolaryzowane liniowo. Wówczas wektor E fali odbitej drga w kierunku prostopadłym do płaszczyzny.

Przykładem polaryzatora drugiego rodzaju jest pryzmat Nicole'a (zwany nikolem) wycięty z kryształu szpatu islandzkiego. Pryzmat jest przecięty i odpowiednio zeszlifowany, a następnie sklejony balsamem kanadyjskim. Promień światła naturalnego s ulega w pryzmacie rozdwojeniu na promień zwyczajny "o' i promień nadzwyczajny "e". Promień zwyczajny padając na powierzchnię balsamu kanadyjskiego pod kątem większym od granicznego ulega całkowitemu wewnętrznemu odbiciu i zostaje pochłonięty przez poczernioną oprawę pryzmatu. Promień nadzwyczajny przechodzi przez warstwę balsamu, ulega w niej nieznacznemu przesunięciu i po załamaniu na tylnej ściance wychodzi z pryzmatu równolegle do promienia padającego s. Drgania wektora E w promieniu zwyczajnym odbywają się
prostopadle do płaszczymy przekroju głównego (x) (zawierającej kierunek osi optycznej i normalną padania). W płaszczyźnie przekroju głównego natomiast, zgodnej z płaszczyzną, odbywają się drgania wektora w promieniu nadzwyczajnym, wychodzącym z nikola. Przy obrocie pryzmatu wokół promienia s o pewien kąt, o taki sam kąt obraca się płaszczyzna drgań wektora światła przechodzącego przez pryzmat.

W niektórych kryształach dwójłomnych współczynnik pochłaniania zależy od orientacji wektora elektrycznego fali świetlnej, tzn. jest różny dla promieni zwyczajnego i nadzwyczajnego i zależy od kierunku rozchodzenia się światła w krysztale. Zjawisko to nazywa się dichroizmem. Jednym z takich kryształów w których można zaobserwować dichroizm jest herapatyt (jodosiarczan chininy). Rozmiary kryształów herapatytu są bardzo małe. Dlatego w celu otrzymania polaryzatora o dużym polu powierzchni stosuje się płytki celuloidowe. w których zatapia się dużą ilość jednakowo zorientowanych kryształów herapatytu. Płytki takie mogą być stosowane np. zamiast nikola i nazwane zostały polaroidami.

Urządzenia służące do określenia stopnia polaryzacji światła nazywają się analizatorami. Jako analizatory są stosowane te same przyrządy, które wykorzystuje się do otrzymania światła spolaryzowanego liniowo (nikole. polaroidy itp.). Każdy analizator (lub polaryzator) można wyobrazić sobie umownie jako kratę, której pręty są równoległe do kierunku drgań wektora . spolaryzowanego przez niego światła. Jeżeli na taką kratę - analizator pada światło naturalne to natężenie I światła przepuszczonego nie ulega zmianie przy obrocie analizatora wokół promienia padającego. Wynika to z tego że w świetle naturalnym żaden z kierunków płaszczyzny drgań nie jest wyróżniony.

Prawo Malusa:

I_a- natężenie światła po przejściu przez analizator

I_p- natężenie światła po przejściu przez polaryzator

k_a- współczynnik przezroczystości analizatora

α-kąt między polaryzatorem a analizatorem

Układ pomiarowy i wykonanie ćwiczenia.

Ćwiczenie wykonałem na zestawie składającym się ze źródła światła Z, polaroidów P i A spełniających rolę polaryzatora i analizatora oraz fotooporu F, który spełnia rolę czujnika reagującego na zmiany natężenia światła.

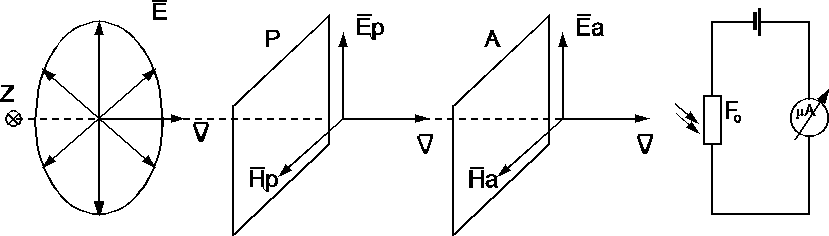
Rysunek schematyczny układu

Wszystkie elementy zostały połączone obudową aby światło zewnętrzne nie wpływało na wyniki pomiarów i umieszczone na ławie optycznej.

Wykonałem 36 pomiarów natężenia światła przechodzącego przez polaryzator i analizator za każdym razem zwiększając kąt między polaryzatorem i analizatorem o 10 , wyniki wpisując do tabeli pomiarów.

Obliczenia.

Niepewność wzorcowania i eksperymentatora dla α:

Δ_eα = 5°

Δ_dα = 10°

Niepewność wzorcowania i eksperymentatora dla I:

Δ_eI = 4 µA

• klasa = 0,5

• ilość działek = 75

• zakres 300 μA

• wartość jednej działki = 4μ

Niepewności standardowe:

Obliczanie niepewności z jakim wyznaczono cos²α.

y=cos²α

I1	I2	I3	I śred	α	cos^2α
[µA]	[µA]	[µA]	[µA]	[º]	[º]
146	144	142	144,00	0	1,00
134	136	132	134,00	10	0,97
114	118	110	114,00	20	0,88
94	94	92	93,33	30	0,75
68	66	64	66,00	40	0,59
44	42	40	42,00	50	0,41
24	22	20	22,00	60	0,25
12	10	10	10,67	70	0,12
6	6	4	5,33	80	0,03
4	4	4	4,00	90	0,00
6	6	6	6,00	100	0,03
16	14	16	15,33	110	0,12
32	30	30	30,67	120	0,25
52	50	50	50,67	130	0,41
76	74	74	74,67	140	0,59
98	96	100	98,00	150	0,75
120	118	120	119,33	160	0,88
130	130	130	130,00	170	0,97
138	134	134	135,33	180	1,00
126	120	124	123,33	190	0,97
108	104	106	106,00	200	0,88
86	84	84	84,67	210	0,75
62	60	60	60,67	220	0,59
40	38	38	38,67	230	0,41
22	20	20	20,67	240	0,25
10	10	10	10,00	250	0,12
4	4	4	4,00	260	0,03
4	4	4	4,00	270	0,00
6	6	6	6,00	280	0,03
16	14	16	15,33	290	0,12
30	30	32	30,67	300	0,25
54	52	52	52,67	310	0,41
76	80	80	78,67	320	0,59
104	104	104	104,00	330	0,75
126	126	128	126,67	340	0,88
140	138	140	139,33	350	0,97

Wykresy.

1.

2.

Wnioski.

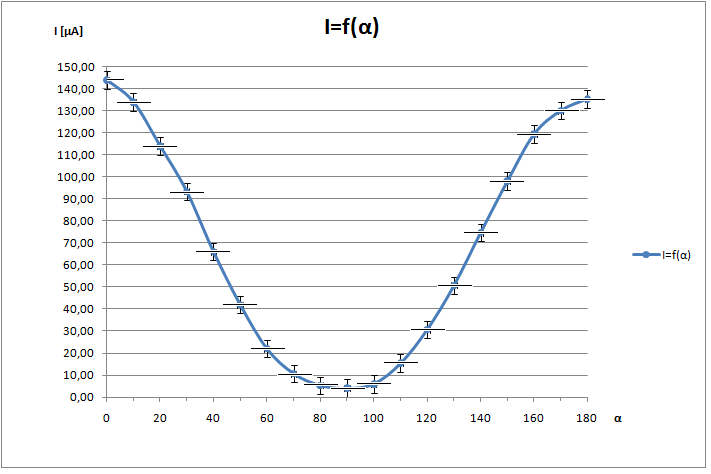
Z wykresu 1 można wywnioskować, że natężenie światła wychodzącego z analizatora jest proporcjonalne do kąta między polaryzatorem a analizatorem i zmienia się okresowo w ramach każdej ćwiartki kąta pełnego.

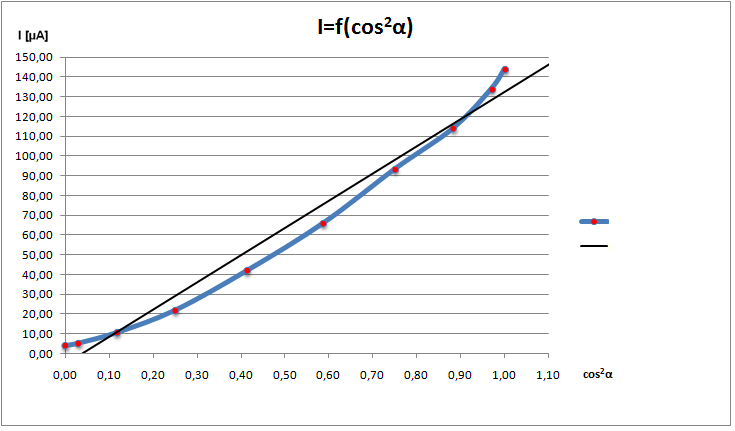
Dowodzi to, że natężenie światła wychodzącego z analizatora jest funkcją okresową kąta między polaryzatorem a analizatorem, natomiast prostoliniowy ( w przybliżeniu) przebieg wykresu 2 potwierdza prawo Malusa, czyli określa tą funkcję jako

k cos2α

gdzie k jest współczynnikiem proporcjonalności. Wyniki ćwiczenia potwierdzają prawo Malusa w praktyce.

Na błąd pomiarów wpływają niedokładność skali kątomierza (najmniejsza działka to 5), oraz błąd i niedokładność wskazań amperomierza ΔI przy pomiarach wartości bliskich 0 µA (dla kąta α = 90 i 270 ) . Poza tym przyczyną nieliniowości drugiej charakterystyki jest to iż mechanizm ustawiania polaryzatorów nie jest idealny, posiada on pewne wady i pomimo ustawienia polaryzatorów prostopadle do siebie w osi optycznej to polaryzatory nie są prostopadłe względem swoich płaszczyzn zewnętrznych.

I=f(cos²α)

liniowy I=f(cos²α)

hhf

I=f(cos²α)

liniowy I=f(cos²α)

---