27

Laboratoria Chemii Fizycznej

ĆWICZENIE NR 38

TEMAT: Wyznaczanie ciepła parowania metodą tensymetryczną

Piotr Tylak

Data: 5.05.2009r.

Godziny zajęć: 12:15 - 16:15

Cel ćwiczenia: obliczenie ciepła parowania na podstawie temperaturowej zależności prężności cieczy.

Wstęp teoretyczny.

Faza - część układu jednolita pod względem chemicznym i fizycznym, oddzielona od innych części wyraźną powierzchnią rozdziału. Może składać się z dowolnej ilości substancji. Może stanowić całość lub może być podzielona na szereg mniejszych jednostek, jednak wymiary fragmentów fazy muszą być większe od molekularnych. Na powierzchni rozdziału występują skokowe zmiany właściwości makroskopowych. Wewnątrz fazy właściwości nie zmieniają się.

Układ - jest to ciało lub zespół ciał poddawanych obserwacji.

Składnik niezależny - jest to każde indywiduum chemiczne tzw. zbiór wszystkich substancji niezależnie od stanu skupienia, których cząsteczki składają się z tych samych rodzajów atomów połączonych ze sobą w takich samych stosunkach.

Liczba stopni swobody - definiuje się ją jako najmniejszą liczbę parametrów intensywnych, które trzeba określić dla wyznaczenia wartości wszystkich pozostałych parametrów intensywnych. Liczbę tę oznacza się symbolem z. Według innego sformułowania jest to liczba parametrów intensywnych, które można niezależnie zmieniać nie powodując zakłócenia równowagi fazowej.

Reguła faz Gibbsa - można ją wyrazić równaniem:

.

s - liczba składników rozdzielonych między f faz układu. Liczbę stopni swobody układu można wyznaczyć sumując liczby parametrów potrzebnych do opisania poszczególnych faz, a następnie odejmując od otrzymanej sumy liczbę tych parametrów, których wartości są wyznaczone przez zależności równowagowe między różnymi fazami.

Jeżeli układ zawiera jeden składnik nie reagujący chemicznie, liczba stopni swobody wynosi z = 3-f. W stanie równowagi mogą więc występować dwie lub trzy fazy.

Dla układu jednoskładnikowego w 2 fazach mamy, więc: z=1-2+2=1 Oznacza to, że jeden z parametrów p lub T można dobrać dowolnie, a drugi przybierze wartość od niego zależną. Zatem wielkości te są od siebie zależne, co można zapisać jako:

f(p,T)=0

Matematycznym wyrazem tej funkcji jest równanie Clausiusa - Clapeyrona:

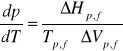
gdzie:

-entalpia przemiany fazowej

-temperatura przemiany fazowej

-zmiana objętości towarzysząca przemianie fazowej

Dla równowagi pomiędzy gazem a cieczą można przyjąć, iż:

Praktycznie, szczególnie ważne są układy zawierające parę nasyconą, tzn. parę pozostającą w równowadze z ciałem stałym. Zakładając, że spełnia ona równanie gazu doskonałego

oraz uwzględniając
, ponieważ
, wzór przybiera postać:

,

gdzie P oznacza ciśnienie pary nasyconej. Gdy ΔH_par = const, po rozdzieleniu zmiennych i scałkowaniu równania otrzymuje się:

Zależność lnp = f(1/T) jest liniowa, a współczynnik kierunkowy jest równy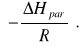

Wyniki pomiarów.

t (°C)	h1 (mmHg)	h2 (mmHg)	T (°K)	1/T	ln pc

Tabela wyników:

t (°C)	T (°K)	h1 (mmHg)	h2 (mmHg)	Pc=h1-h2	1/T	ln(pc)
24	297	152	117	35	0,0033670	3,5553480
28,5	301,5	158	112	46	0,0033167	3,8286414
34,5	307,5	164	105	59	0,0032520	4,0775374
40,5	313,5	171	98	73	0,0031898	4,2904594
45,5	318,5	179	91	88	0,0031397	4,4773368
52,5	325,5	194	77	117	0,0030722	4,7621739

Wykres:

Obliczenia:

Wykres przedstawia liniową zależność określoną wzorem:

ln(p_c) = -3959,5 (1/T) + 16,926

Ciepło parowania toluenu oblicza się ze wzoru:

,

gdzie:

b - współczynnik kierunkowy prostej

R - stała gazowa.

b = -3959,5

ΔH_p = 8,314
ּ3959,5
=

Wartość ciepła parowania toluenu odczytana z tablic wynosi:

ΔH_{p =}
.

Wartość ciepła parowania otrzymana z obliczeń:

ΔH_p =
.

Wnioski:

Celem ćwiczenia było wyznaczenie ciepła parowania toluenu metodą tensometryczną

Wykres pokazuje liniowa zależność lnp = f(1/T). Zależność tą opisuje równanie

ln(p_c) = -3959,5 (1/T) + 16,926.

Otrzymana z doświadczalna wartość parowania wynosi ΔH_p =
i jest zbliżona do wartości literaturowej która wynosi ΔH_{p =}
.

Różnica między wartością literaturowa, a doświadczalną ciepła parowania może być spowodowana błędem odczytów poziomów słupka rtęci.

---