ROZKŁADY STATYSTYKI Z PRÓB

Populacja generalna - skończony lub nieskończony zbiór elementów.

Interesują nas parametry populacji - liczbowe charakterystyki całej populacji. Najczęściej są to średnia (oznaczamy przez m), odchylenie standardowe (σ), frakcja elementów wyróżnionych ze względu na interesującą nas cechę (p).

Badania statystyczne - pełne, częściowe. Na podstawie próby losowej wnioskujemy o populacji. Wnioskowanie wymaga pewną podstawę teoretyczną.

Statystyką z próby nazywa się liczbową charakterystykę próby np. średnia
, odchylenie standardowe s, lub frakcję elementów wyróżnionych w próbie,
. Wnioskowanie o tym, jakie są parametry populacji opiera się na znajomości statystyk z próby. Jeśli statystyka z próby jest wykorzystywana do oszacowania parametru populacji nazywa się ją estymatorem tego parametru.

Oceną (szacunkiem) parametru jest konkretna wartość liczbowa estymatora z danej próby.

Średnia z próby,
, jest statystyką używaną jako estymator średniej w populacji m.

Odchylenie standardowe z próby, s, jest statystyką używaną jako estymator odchylenia standardowego w populacji σ.

Frakcja elementów wyróżnionych ze względu na interesującą nas cechę w próbie,
, jest statystyką używaną jako estymator frakcji elementów wyróżnionych w populacji p.

Statystyka z próby jest zmienną losową, ponieważ jej konkretna wartość zależy od tego, jaką w konkretnym przypadku próbę wylosowaliśmy.

Rozkład statystyki z próby jest rozkładem prawdopodobieństwa wszystkich możliwych wartości, jakie ta statystyka może przyjąć, jeżeli obliczamy je na podstawie badania n-elementowych losowych prób, pobranych z określonej populacji.

Rozkład średniej z próby pochodzącej z rozkładu normalnego

.

Centralne twierdzenie graniczne: jeśli badana cecha ma w populacji nieznany rozkład o średniej m i odchyleniu standardowym σ, to rozkład średniej z n-elementowej próby,
, dąży do rozkładu normalnego o średniej m i odchyleniu standardowym
, gdy liczebność próby wzrasta nieograniczenie (czyli dla dostatecznie dużych n, najczęściej dla celów praktycznych wystarczy n>30).

Standaryzacja średniej z próby pozwala otrzymać zmienną o standardowym rozkładzie normalnym:

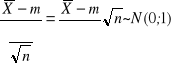
Rozkład wskaźnika struktury (frakcji elementów wyróżnionych)

W praktycznych zastosowaniach często interesującą charakterystyką jest tak zwana frakcja elementów wyróżnionych (wskaźnik struktury,
. Pokazuje ona, jaką część rozpatrywanej populacji stanowią elementy o interesującej nas cesze.

Wyobraźmy sobie, że dysponujemy populacją, w której frakcja elementów wyróżnionych wynosi p. Z populacji tej losujemy n-elementową próbę. Frakcja elementów wyróżnionych w próbie,
, ma w przybliżeniu rozkład normalny z parametrami: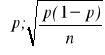
.

Statystyki z próby

Średnia:

Odchylenie standardowe: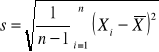
lub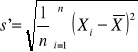

Frakcja elementów wyróżnionych w próbie:
, X - liczba elementów wyróżnionych w próbie, n - liczebność próby

ESTYMACJA PUNKTOWA I PRZEDZIAŁOWA. PRZEDZIAŁY UFNOŚCI.

Estymacja punktowa polega na znalezieniu takiej liczby, która w najbardziej wiarygodny sposób wyraża wartość poszukiwanego, nieznanego parametru.

,
nazywamy średnim błędem szacunku parametru m

Jeśli próba jest duża, a σ jest nieznane, to możemy zastosować przybliżenie, σ ≈ S.

Estymacja (ocena) przedziałowa polega na skonstruowaniu przedziału, który z dużym prawdopodobieństwem (bliskim jedności) zawiera nieznaną, prawdziwą wartość poszukiwanego parametru populacji generalnej.

Przedziałem ufności nazywamy przedział liczbowy, o którym przypuszczamy, że mieści się w nim nieznany parametr populacji. Z przedziałem tym związana jest miara ufności (pewności), że ten przedział naprawdę zawiera interesujący nas parametr, zwaną poziomem ufności (1-α).

Przykład. W UE obowiązują normy dotyczące średnicy jabłek. Pewien polski sadownik zastanawiając się, czy będzie mógł konkurować na rynku UE postanowił sprawdzić, jaka jest przeciętna średnica jabłek z jego sadu. Rozkład średnicy jabłek jest normalny z parametrami m i σ. Wylosował on próbę złożoną z 64 jabłek i zmierzył ich średnicę. Na tej podstawie obliczył, że średnica jabłek mierzona średnią arytmetyczną wynosi 7,23cm a odchylenie standardowe S=1,12cm. Jaka jest więc przeciętna średnica wszystkich jabłek w sadzie sadownika?

Próba jest duża (n=64), więc możemy zastosować przybliżenie, że σ ≈ S. Wykorzystując to przybliżenie, możemy powiedzieć, że przeciętna średnica wszystkich jabłek w sadzie sadownika wynosi 7,23cm z dokładnością (średnio) do
=0,14cm, co możemy zapisać: m ≈ 7,23cm ± 0,14cm.

Estymacja przedziałowa wybranych parametrów

Przedziały ufności dla średniej w populacji, gdy odchylenie standardowe populacji σ jest znane:

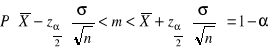
Przedziały ufności dla średniej w populacji, gdy odchylenie standardowe populacji σ jest nieznane, a próba jest mała:

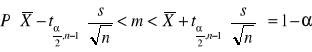
Przedziały ufności dla średniej w populacji, gdy odchylenie standardowe populacji σ jest nieznane, a próba jest duża:

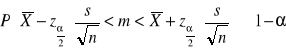
d=
nazywamy maksymalnym (bezwzględnym) błędem szacunku parametru m

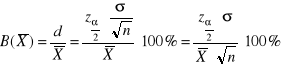
nazywamy względnym błędem szacunku parametru m

Jeśli
<5%, to oszacowanie charakteryzuje się dużą precyzją, jeśli natomiast
przekracza 10%, to nie należy uogólniać wyniku z próby na całą populację.

Minimalna liczebność próby

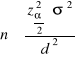
Przedziały ufności dla wskaźnika struktury p w populacji, gdy próba jest duża (n>100):

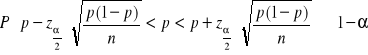
d=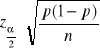
maksymalny (bezwzględny) błąd szacunku parametru p (może być podany w %!)

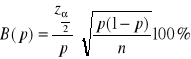
względny błąd szacunku parametru p

Minimalna liczebność próby

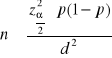
jeśli znamy rząd wielkości p,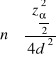
, jeśli nie znamy rzędu wielkości p.

Przedziały ufności dla odchylenia standardowego w populacji σ, gdy próba jest mała, a

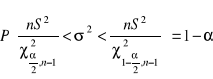
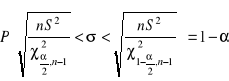
Przedziały ufności dla odchylenia standardowego w populacji σ, gdy próba jest duża, a
,

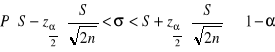
d=
nazywamy maksymalnym (bezwzględnym) błędem szacunku parametru σ

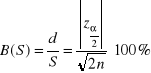
nazywamy względnym błędem szacunku parametru σ

Zadania:

1.Wiadomo, że wzrost mężczyzn ma rozkład N(m,σ). Na podstawie 81-elementowej próby losowej obliczono, że średnia wzrostu wynosi
=175 cm, przy odchyleniu standardowym s=25cm.

a) Przeprowadzić estymację punktową średniej m w populacji;

b) Wybierając poziom ufności 0,90 przeprowadzić estymację przedziałową średniej m w populacji.

c) Ile wynosi średni błąd szacunku parametru m?

d) Ile wynosi maksymalny (bezwzględny) błąd szacunku parametru m?

e) Ile wynosi względny błąd szacunku parametru m?

2. Spośród wszystkich studentów WSFiZ wybrano w sposób losowy 49-studentów i obliczono, że średnia ocen z poprzedniego semestru wynosi
=3,82, przy odchyleniu standardowym s=0,53. Przyjmując współczynnik ufności 0,90 zbudować przedział ufności dla średniej ocen w całej populacji studentów WSFiZ. Jak zmieni się długość przedziału, gdy zwiększymy poziom ufności?

3. Zbadano 16-elementową grupę pacjentów poddanych leczeniu nowym lekiem. Średni czas poprawy stanu zdrowia wynosi 6 dni z odchyleniem standardowym 1 dzień. Na poziomie ufności 0,95 przeprowadzić estymacje przedziałową średniego czasu poprawy pacjentów leczonych nowym lekiem.

4. Jeśli n=81,
=50, s=5; 1-α=0,9545 zbudować przedział ufności dla wartości przeciętnej w populacji.

5. Na podstawie dotychczasowych badań ustalono, że wydatki na rozrywkę w Ośrodku wypoczynkowym mają rozkład normalny z odchyleniem standardowym σ =50zł. Wśród ilu wypoczywających należy przeprowadzić badanie, aby na poziomie ufności 0,95 oszacować przedziałowo średnią wydatków na rozrywkę z dopuszczalnym maksymalnym błędem 10 zł?

6. Agencja badania opinii publicznej postanowiła ustalić odsetek zwolenników partii „Niebieskie migdały” spośród wszystkich mieszkańców miasta X z maksymalnym błędem bezwzględnym 5%. Zakładając poziom ufności 0,90 ustalić minimalną liczebność próby.

7. Wiadomo, że czas wykonywania pewnej operacji (w min) w pewnym przedsiębiorstwie po wprowadzeniu modernizacji ma rozkład N(m;4). Na podstawie 50 elementowej próby dokonano estymację przedziałową parametru m na poziomie ufności 0,90. Czy próba jest wystarczająco duża, aby przy estymacji nie popełnić błędu większego niż 0,5 min?

8. Wiadomo, że waga soków (w kg) napełnianych przez automat ma rozkład N(m;0,02). Na podstawie wyników z 64-elementowej próby losowej obliczono
=0,98kg. Obliczyć średni błąd szacunku parametru m. Na poziomie ufności 0,9545 przeprowadzić estymację przedziałową średniej wagi soków. Policzyć względny błąd szacunku parametru.

9.W celu zbadania miesięcznego użycia wody (w m³) przez mieszkańców na pewnym warszawskim osiedlu wylosowano 60 mieszkań i otrzymane wyniki zapisano w poniższej tablicy:

Zużycie wody	Liczba mieszkań
<0; 6>	5
(6; 12>	11
(12;18>	22
(18;24>	18
(24;30>	4

Przyjmując współczynnik ufności 0,90 zbudować przedział ufności dla średniego zużycia wody we wszystkich mieszkaniach badanego osiedla.

10. Z raportu Komisji Edukacji Narodowej wynika, że w marcu 2004 roku spośród 500 losowo wybranych uczniów szkół warszawskich 342 twierdzą, że preferują nową maturę przed starą. Ocenić na poziomie ufności 0,95 nieznany odsetek uczniów w całej Warszawie, którzy wolą zdawać maturę według nowych reguł..

11. Zarząd przedsiębiorstwa X planuje wyemitować obligacje. Wcześniej jednak chce oszacować procent osób zainteresowanych ich kupnem z błędem nie przekraczającym 3%. Ile osób należy wylosować do próby losowej, aby nie przekroczyć tego błędu na poziomie ufności 0,95.

12. Na poziomie ufności 0,98 określić, jaka powinna być minimalna liczebność próby niezbędna do oszacowania odsetka osób, które darzą zaufaniem polityka M z dopuszczalnym błędem 5%. Jako wstępne przyjmujemy wyniki ostatniego sondażu, w którym zaufanie do tego polityka deklarowało 30% ankietowanych osób.

dr Rumiana Górska

1

---