IMIĘ I NAZWISKO |
Ćwiczenie M-1
WYZNACZANIE PRZYSPIESZENIA ZIEMSKIEGO PRZY POMOCY WAHADŁA MATEMATYCZNEGO |
||
ROK I KIERUNEK |
|
||
|
OCENA |
OCENA |
OCENA |
PROWADZĄCY |
DATA
PODPIS |
DATA
PODPIS |
DATA
PODPIS
|
1. Cel ćwiczenia
Przeprowadzenie pomiaru przyśpieszenia ziemskiego (g) przy pomocy wahadła matematycznego.
2. Część teoretyczna
Przyspieszenie ziemskie (grawitacyjne)
Przyspieszenie, którego doznają wszystkie ciała na ziemi, zwane jest przyśpieszeniem ziemskim lub grawitacyjnym. Oznaczane jest małą literą g. Jest ono wielkością wektorową; kierunek wektora tego przyspieszenia jest pionowy i zwrócony prostopadle ku środkowi kuli ziemskiej.
Wartość przyspieszenia ziemskiego nie jest jednakowa na całej kuli ziemskiej. Zmienia się wraz ze zmianą szerokości geograficznej oraz wysokości nad poziomem morza. W obliczeniach przyjmuje się wartość przyspieszenia ziemskiego mierzoną na poziomie morza oraz odpowiadającą szerokości 45º lub jej wartość rzeczywistą, występującą w rozpatrywanym punkcie Ziemi.
Z przyciąganiem ziemskim nierozerwalnie połączone jest prawo grawitacji (ciążenia powszechnego), sformułowane przez Newtona
Z prawa tego wiemy, że wartość przyspieszenia ziemskiego maleje w miarę oddalania się od Ziemi. Treść prawa grawitacji jest następująca:
„Wszystkie ciała przyciągają się wzajemnie. Siła F wzajemnego przyciągania się dwóch ciał jest wprost proporcjonalna do wartości ich mas m1 i m2 i odwrotnie proporcjonalna do kwadratu odległości r pomiędzy środkami ich mas.”
![]()
Wartość współczynnika proporcjonalności G, zwanego s t a ł ą g r a w i t a - c y j n ą wyznaczono doświadczalnie i wynosi ona:
6,65•10-8 cm3/g s2
Siła ciążenia działa między wszystkimi bez wyjątku ciałami, np. dowolne ciało i Ziemia. Działanie sił przyciągania jest wzajemne, przy czym siły te mają kierunek prostej łączącej środki obydwu mas.
Siła przyciągania grawitacyjnego dowolnego ciała o masie m na powierzchni Ziemi równa jest ciężarowi ciała
Q = mg
Zgodnie z prawem ciążenia powszechnego siła ta równa jest:
![]()
![]()
gdzie:
G - stała grawitacyjna
m - masa ciała
M - masa Ziemi
r - promień Ziemi
h - wysokość ciała nad poziomem morza
R - odległość os środka ciał
Wartość przyspieszenia zmienia się również w skutek ruchu obrotowego Ziemi wokół własnej osi. Ziemia jest układem nieinercjalnym, więc dodatkowo, na wszystkie ciała działa siła odśrodkowa bezwładności, która jest prostopadła do osi obrotu Ziemi i jest tym większa im większa jest odległość od tej osi.
W wyniku działania siły bezwładności i spłaszczenia Ziemi wartość przyspieszenia ziemskiego wynosi w przybliżeniu:
na biegunie 9.83 m/s2
na równiku 9.78 m/s2
Wahadło matematyczne
Wahadłem matematycznym nazywamy punkt materialny o masie m i ciężarze Q zawieszony na nieważkiej i nierozciągliwej nici o długości l. W położeniu wychylonym na punkt ten działa składowa siły ciążenia, siła poruszająca ![]()
, gdzie ciężar Q wynosi mg.
Łącząc powyższe równania i podstawiając
![]()
gdzie x jest wychyleniem punktu w stosunku do położenia równowagi, otrzymujemy:
![]()
Ponieważ m, l oraz g są dla określonego wahadła wielkościami stałymi, a więc siła poruszająca F jest wprost proporcjonalna do wielkości wychylenia x. Wynika stąd, że ruch wahadłowy jest dla małych wychyleń (![]()
) ruchem harmonicznym.
Przyśpieszenie ruchu harmonicznego wyrażone jest równaniem:
![]()
stąd siła poruszająca
![]()
Porównując tę wartość z uprzednio wyprowadzonym równaniem otrzymujemy
![]()
a stąd
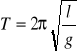
Z powyższego równania zauważamy, że okres wahań wahadła matematycznego nie zależy od amplitudy i masy wahadła, natomiast zależy od jego długości i wartości danego w rozpatrywanym miejscu przyspieszenia ziemskiego.
Ruch harmoniczny
Jest to szczególny, bardzo ważny przypadek ruch drgającego, w którym ciało periodycznie zmienia swoje położenie, pozostając stale w pobliżu położenia równowagi. Można powiedzieć, że ciało jest w ruchu harmonicznym wokół położenia równowagi x0 = 0, jeżeli wychylenie x z tego położenia jest sinusoidalną funkcją czasu:
![]()
gdzie A oznacza maksymalne wychylenie z położenia równowagi i nosi nazwę amplitudy, ώ - częstość kołowa, a funkcja (ώt + φ) nazywa się fazą, przy czym φ jest fazą początkową (dla t = 0)
Przedstawię teraz sposób wyprowadzenia powyższego wzoru.
Porównując ze sobą wzór na siłę II Zasady Dynamiki Newtona (F = ma), gdzie ![]()
oraz wzór na silę sprężystości (F = -kx) otrzymujemy:
![]()
Po obustronnym podzieleniu przez masę oraz podstawieniu ![]()
otrzymujemy:
![]()
Rozwiązaniem tego równania jest właśnie wzór:
![]()
Różniczkując powyższe równanie dwukrotnie względem czasu otrzymujemy:
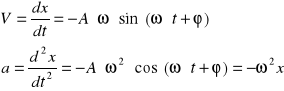
3. Przyrządy pomiarowe.
Wahadło matematyczne wraz z wyposażeniem
Stoper
4. Przebieg ćwiczenia
Wprawiłem wahadło w drgania poprzez wychylenie go o kąt 5°.
Zmierzyłem czas trwania 50 okresów T.
Skróciłem nić wahadła o około 1/5 poprzez uchwycenie jej przy pomocy
ruchomego zacisku długości i ponownie zmierzyłem czas trwania 50 okresów T.
Odczytałem wartość d, o jaką skróciłem nić wahadła.
Powtórzyłem pomiary z punktów 2-4 dla trzech innych położeń zacisku na nici
wahadła.
Wyniki pomiarów przedstawiłem w tabelce.
Wykonałem cztery obliczeń przyspieszenia ziemskiego. Obliczyłem średnią wartość
Obliczyłem błąd ∆g stosując metodę Studenta - Fishera do wyników gi z
założonym poziomem ufności ά = 0,95
5. Wyniki pomiarów
Nr pomiaru |
0 |
1 |
2 |
3 |
4 |
długość o jaką skrócono nić wahadła d [m] |
0 |
0,1 |
0,2 |
0,3 |
0,4 |
długość nici wahadła l [m] |
0,8 |
0,7 |
0,6 |
0,5 |
0,4 |
czas trwania 50 okresów T [s] |
89 |
82 |
77 |
71 |
63 |
czas trwania jednego okresu T [s] |
1,78 |
1,64 |
1,54 |
1,42 |
1,26 |
6. Obliczenia
Wykonuje cztery obliczenia przyśpieszenia ziemskiego według wzoru:
![]()
![]()
![]()
![]()
![]()
Obliczam wartość średnią
![]()
![]()
Obliczam błąd ∆g stosują c metodę Studenta - Fishera do wyników gi z założonym poziomem ufności ά = 0.95
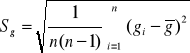
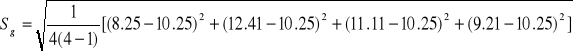
![]()
![]()
Mnożę Sg przez współczynnik studenta Fishera tnά dla założonego poziomu ufności
ά = 0.95 równy 2.8
![]()
Wartość przyspieszenia ziemskiego jest równa w przybliżeniu:
![]()
![]()
7. Wnioski
Okres drgań wahadła matematycznego zależy od jego długości. Zauważyłem, że im bardziej skracałem nić tym bardziej okres wahadła się skracał, a jego ruchy były coraz szybsze.
Wartość przyspieszenia ziemskiego, którą obliczyłem odbiega znacznie od wartości podawanej w tablicach. Przyczyn może być kilka:
określenie i ustawienie precyzyjnej długości wahadła było niemożliwe
pomiędzy włączaniem i wyłączaniem stopera, a wprawianiem wahadła w ruch mogła wystąpić niewielka, lecz znacząca różnica czasu.
przy krótkiej długości wahadła punkt materialny ciężko było wprawić w drgania w płaszczyźnie pionowej.
wartość podana przez tablicę jest obliczana przez najnowocześniejszy sprzęt w najlepiej wyposażonych laboratoriach świata. Wszystkie pomiary są niezwykle precyzyjne.
![]()
![]()
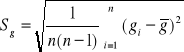
Wyszukiwarka
Podobne podstrony:
II06 Wyznaczanie przyspieszenia ziemskiego przy pomocy wahadla rewersyjnego
Wyznaczenie przyśpieszenia ziemskiego przy pomocy wahadła fizycznego2
2 Wyznaczanie przyśpieszenia ziemskiego przy pomocy wahadła rewersyjnego oraz wyznaczanie modułu spr
Wyznaczenie przyśpieszenia ziemskiego przy pomocy wahadła fizycznego
II06 Wyznaczanie przyspieszenia ziemskiego przy pomocy wahadla rewersyjnego
Wyznaczanie przyspieszenia ziemskiego przy pomocy wahadła prostego, Pollub MiBM, fizyka sprawozdania
Wyznaczanie przyspieszenia ziemskiego przy pomocy wahadła prostego, Fizyka
14, Studia, Pracownie, I pracownia, 14 Wyznaczanie przyspieszenia ziemskiego przy użyciu wahadła rew
Wyznaczanie przyspieszenia ziemskiego za pomoca wahadła matematycznego, studia, fizyka
Wyznaczanie przyspieszenia ziemskiego przy pomocy spadkownicy (2)
Wyznaczenie przyspieszenia ziemskiego za pomocą wahadła rewersyjnego2, Studia, laborki fizyka (opole
WYZNACZANIE PRZYSPIESZENIA ZIEMSKIEGO PRZY UŻYCIU WAHADŁA REWERSYJNEGO
Pomiar przyśpieszenia ziemskiego przy pomocy wahadła rewersy
1 Wyznaczanie wartości przyspieszenia ziemskiego g przy użyciu wahadła matematycznego instr przys
więcej podobnych podstron