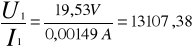Wyznaczanie współczynnika samoindukcji cewki i pojemności kondensatora.
Ćwiczenie nr 44
Cel ćwiczeń
Celem mojego doświadczenia jest zapoznanie się ze zjawiskami zachodzącymi w cewce i w kondensatorze w obwodach prądu stałego i zmiennego.
2. Wprowadzenie
Cewka w obwodzie prądu stałego i zmiennego.
Wartość natężenia w obwodzie prądu zmiennego jest wyrażnie mniejsza niż w obwodzie prądu stałego. Oznacza to, że opór cewki w obwodzie prądu stałego jest mniejszy niż w obwodzie prądu zmiennego.
Cewka włączone do obwodu prądu stałego zachowuje się jak opór omowy, którego wartość R zależy od wymiarów geometrycznych i rodzaju przewodnika:
![]()
gdzie: ![]()
- opór właściwy
l- długość
s- pole przekroju
Po włączeniu cewki do obwodu prądu zmiennego pojawia się dodatkowy opór indukcyjny, związany ze zjawiskiem samoindukcji.
Przepływając przez cewkę, zmieniający się w czasie prąd powoduje powstawanie zmiennego strumienia magnetycznego, który w uzwojeniu cewki będzie indukował SEM. Ten szczególny przypadek zjawiska indukcji elektromagnetycznej, kiedy to SEM indukcji powstaje w tej samej cewce, przez którą płynie zmieniający się prąd, nazywa się samoindukcją lub indukcją własną. SEM samoindukcji, jako szczególny przypadek indukcji elektromagnetycznej, określona jest wzorem:
![]()
gdzie:![]()
szybkość zmian natężenia prądu
L- współczynnik samoindukcji
Indukcyjność własną cewki wyraża się w układzie jednostek SI również w henrach 1H=1V*s*A-1. Wartość L zależy od geometrycznego kształtu obwodu, jego rozmiarów i przenikalności magnetycznej ośrodka. W przypadku długiego solenoidu.
![]()
gdzie: n- liczba zwojów
μr - przenikalność magnetyczna ośrodka wewnątrz solenoidu
μ0 - przenikalność magnetyczna próżni
l- długość
S- pole przekroju
Zgodnie z regułą Lenza, prąd, samoindukcyjny w każdej chwili stara się przeciwdziałać zmianie prądu płynącego w obwodzie i dlatego cewka wykazuje dodatkowy opór samoindukcyjny RL. Z prawa Kirchoffa można wyprowadzić, że w przypadku zewnętrznego źródła prądu sinusoidalnie zmiennego o częstości kołowej ω opór indukcyjny cewki o współczynniku samoindukcji L wyraża się wzorem:
RL=L*ω
Gdzie: ω- 2Пf
f- częstotliwość zmian prądu (f=50Hz)
Jeśli opór omowy cewki wynosi R, to jej całkowity opór Z w obwodzie prądu zmiennego (impedancja, zawada) obliczamy jako sumę geometryczną oporu R i oporu indukcyjnego RL:
Z=![]()
Kondensator w obwodzie prądu zmiennego.
Jeżeli podłączymy kondensator szeregowo połączony z żarówką do źródła prądu stałego, żarówka rozbłyśnie tylko na moment, bowiem w obwodzie płynie prąd jedynie do momentu naładowania kondensatora. Po naładowaniu okładek prąd nie płynie-w obwodzie prądu stałego kondensator stanowi praktycznie nieskończenie duży opór. Inaczej jest, jeśli jako źródła prądu użyjemy generatora prądu zmiennego. Wraz ze zmianą prądu w obwodzie zmienia się ładunek na okładkach kondensatora. Naprzemienne ładowanie i rozładowywanie się kondensatora w obwodzie umożliwia przepływ prądu, którego amplituda jest proporcjonalna do pojemności kondensatora C, gdyż zgodnie z definicją pojemności, C=Q/U , im większa pojemność tym większy ładunek Q może być zgromadzony na okładkach. Opór pojemnościowy Rc jest więc tym mniejszy im większa jest pojemność C. Gdy mamy źródło prądu sinusoidalnie zmiennego, Rc wyraża się wzorem;
![]()
Widzimy że opór pojemnościowy jest także odwrotnie proporcjonalny do częstości kołowej zmian prądu. Im większa wartość ω tym mniejszy ładunek zdąży zgromadzić się na kondensatorze podczas jego ładowania i tym mniejsze będzie napięcie przeciwstawiające się przepływowi prądu.
Jeśli w obwodzie prądu zmiennego występuje opór omowy R i kondensator o pojemności C, to całkowity opór, czyli impedancję ωobliczamy ze wzoru:
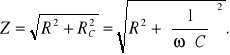
Cewka i kondensator w obwodzie prądu zmiennego.
Gdy obwód zbudowany jest z oporu omowego R, cewki o współczynniku samoindukcji L i kondensatora o pojemności C (elementy połączone są szeregowo) to impedancja takiego obwodu wynosi:
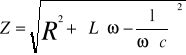
Dla obwodu prądu zmiennego słuszne jest również prawo Ohma. Impedancja Z spełnia zależność:
![]()
gdzie: Us i Is oznaczają skuteczne wartości napięcia i natężenia prądu.
3. Obliczenia
I. Wyznaczenie oporu omowego cewki.
Nr pomiaru, i |
1 |
2 |
3 |
Napięcie Ui |
19,31 V |
15,08 V |
10,30 V |
Natężenie Ii |
3,28 mA |
2,57 mA |
1,73 mA |
Opór Ri |
5887,19 |
5867,70 |
5953,76 |
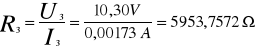
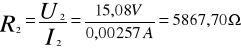
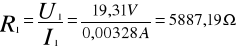
II. Wyznaczanie impedancji i współczynnika samoindukcji cewki.
Nr pomiaru, i |
1 |
2 |
3 |
Napięcie Ui |
19,53 V |
15,27 V |
10,57 V |
Natężenie Ii |
1,49 mA |
1,24 mA |
0,94 mA |
Impedancja Zi |
Z1= |
Z2= |
Z3= |
Współ. samoind. Li |
37,29 H |
34,48 H |
30,38 H |
Wartość średnia współczynnika samoindukcji L |
34,05 H |
||
![]()
![]()
![]()
![]()
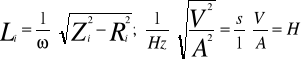
III. Wyznaczanie impedancji i pojemności kondensatora
Nr pomiaru, i |
1 |
2 |
3 |
Napięcie Ui |
19,73 V |
15,90 V |
10,41 V |
Natężenie Ii |
29,2 mA |
23,5 mA |
15,3 mA |
Impedancja Zi |
Z1= |
Z2= |
Z3= |
Poj. kondensatora Ci |
4,713 |
4,706 |
4,68 |
Wartość średnia pojemności kondensatora, C |
4,7 |
||
![]()
F
![]()
F
![]()
F
![]()
![]()
F
4. Rachunek błędu.
Maksymalny błąd bezwzględny pojedynczego pomiaru, R, Z, L, C obliczam metodą różniczki zupełnej.w przypadku mierników cyfrowych dokładność jest równa 1% wartości mierzonej dla prądu stałego i 1,5% wartości mierzonej dla prądu zmiennego.
Opór cewki Ri
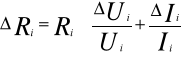
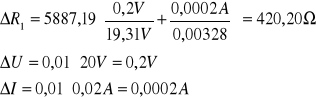
Impedancja Zi
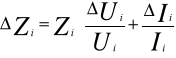
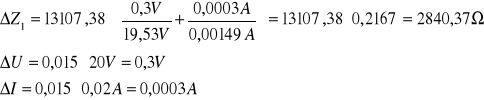
Współczynnik samoindukcji Li
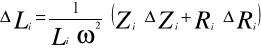
![]()
Pojemność kondensatora Ci. Obliczam ze wzoru:
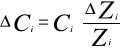
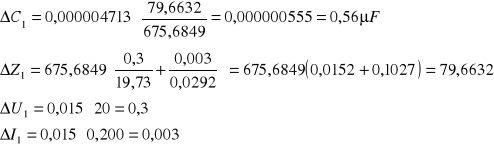
5. Wnioski
Natężenie prądu płynącego przez zwojnicę w obwodzie prądu stałego jest wyraźnie większe niż natężenie w obwodzie prądu zmiennego. Oznacza to, że opór cewki jest mniejszy w obwodzie prądu stałego w porównaniu do oporu w obwodzie prądu zmiennego.
Błędy pomiarowe mogły być spowodowane:
Niedokładnością przyrządów pomiarowych
Niedokładnym odczytaniem pomiarów
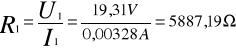
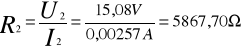
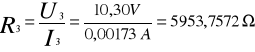
![]()
![]()
![]()
![]()
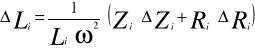
Wyszukiwarka
Podobne podstrony:
równoważnik miedzi (spraw.), Studia SGGW, WNoŻ Inżynierskie 2008-2012, Sem II, Fizyka
równoważnik miedzi (spraw.), Studia SGGW, WNoŻ Inżynierskie 2008-2012, Sem II, Fizyka
Zestaw 3, Studia SGGW, WNoŻ Inżynierskie 2008-2012, Sem II, Chemia organiczna
Zestaw 1, Studia SGGW, WNoŻ Inżynierskie 2008-2012, Sem II, Chemia organiczna
Towary - Test odp nowe pyt, Studia SGGW, WNoŻ Inżynierskie 2008-2012, Sem V, Fakultety, towarozn
analiza 02, Studia SGGW, WNoŻ Inżynierskie 2008-2012, Sem IV, Ocena jakości
Analiza 08, Studia SGGW, WNoŻ Inżynierskie 2008-2012, Sem IV, Ocena jakości
toksyka 02, Studia SGGW, WNoŻ Inżynierskie 2008-2012, Sem IV, Toksykologia
Energia 03, Studia SGGW, WNoŻ Inżynierskie 2008-2012, Sem IV, Gospodarowanie Energią
Ekologia 2, Studia SGGW, WNoŻ Inżynierskie 2008-2012, Sem VI, ekologia
BAKTERIE MLEKOWE 2009, Studia SGGW, WNoŻ Inżynierskie 2008-2012, Sem VI, Fakultety, Bakterie mlekowe
Ekol. ochrona środ.zal.2011, Studia SGGW, WNoŻ Inżynierskie 2008-2012, Sem VI, ekologia
Ekologia 2, Studia SGGW, WNoŻ Inżynierskie 2008-2012, Sem VI, ekologia
polityka 4, Studia SGGW, WNoŻ Inżynierskie 2008-2012, Sem VI, Fakultety, Polityka wyzywienia
BRĄZOWIENIE ENZYMATYCZNE I NIEENZYMATYCZNE W14, Studia SGGW, WNoŻ Inżynierskie 2008-2012, Sem III, C
Energia 01, Studia SGGW, WNoŻ Inżynierskie 2008-2012, Sem IV, Gospodarowanie Energią
ROZTWORY BUFOROWE O ZNANYM pH W 12, Studia SGGW, WNoŻ Inżynierskie 2008-2012, Sem III, Chem żywn
Polityka2a, Studia SGGW, WNoŻ Inżynierskie 2008-2012, Sem VI, Fakultety, Polityka wyzywienia
Kwantowanie energii W13, Studia SGGW, WNoŻ Inżynierskie 2008-2012, Sem III, Chem żywn
więcej podobnych podstron