POLITECHNIKA CZĘSTOCHOWSKA

Laboratorium Automatyki

Temat :Linie pierwiastkowe.

Specjalność: IE gr II

Czwartek 8-10

Skład grupy :

Sroka Sebastian

Ptak Arkadiusz

1. Cel ćwiczenia

Celem ćwiczenia jest zapoznanie się z metodą linii pierwiastkowych i wykorzystanie jej do syntezy układu regulacji z niestabilnym obiektem.

2. Przebieg ćwiczenia.

Ćwiczenie polegało na modelowaniu obiektów regulacji i obserwowaniu wykresów na ekranie monitora, do wykonania ćwiczenia wykorzystano szereg instrukcji które następnie wprowadzono do programu MatLab. Wszystkie wykonane operacji zostały przeprowadzone na zasadzie symulacji komputerowej.

3. Zadanie.

Zaprojektować sposób stabilizowania odwróconego wahadła pokazanego na poniższym rysunku. Sygnałem sterującym ma być przyspieszenie wózka, którego masę można pominąć, a wielkością mierzoną - odchylenie θ.

4. Przebieg ćwiczenia.

Transmitancja obiektu badanego wynosi:

Wykres 1. Linie pierwiastkowe - obiekt badany:

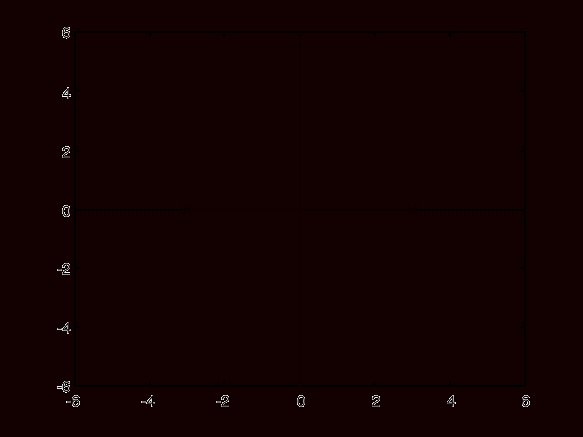
Z wykresu odczytano wzmocnienie K układu, dla którego wystąpią bieguny:

1. rzeczywiste: K1 = -2.7113; R = 2.5077; R = -2.5077.

2. urojone: K2 = -8.0325; R = 0 + 0.9836i; R = 0 - 0.9836i.

Wykres 2. Odpowiedź układu ( dla K1) na warunek początkowy:

Transmitancja wynosi:

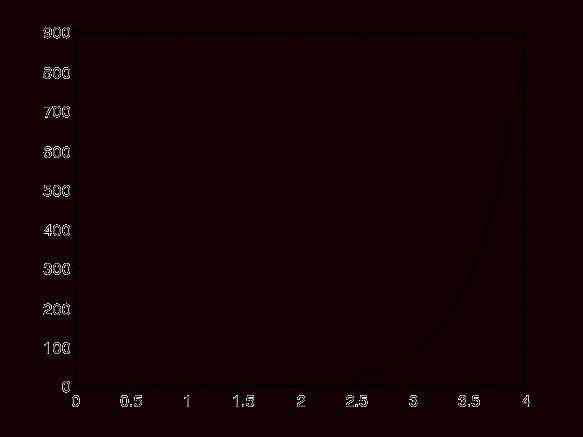
Wykres 3.Odpowiedź układu ( dla K2) na warunek początkowy:

Transmitancja wynosi:

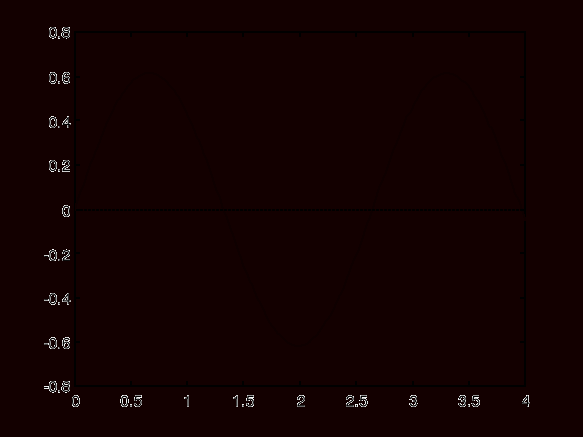
Zadane parametry odpowiedzi skokowej:

- Tr = 0.400 czas narastania

- Mp = 15 przeregulowanie

- Ts = 2 czas ustalania

- omegan = 1.8/Tr = 4.500 pulsacja naturalna drgań nietłumionych

- sigma = 4.6/Tr = 2.300 względny współczynnik tłumienia

- zeta = sigma/omegan = 0.5111 współczynnik tłumienia

- omegad = omegan⋅sqrt(1-zeta²) pulsacja drgań własnych

Dobieramy idealny regulator PD o transmitancji:

G(s) = Kp + Kd⋅s

gdzie: Kd = -4.600, Kp = -29.250,czyli:

G(s) = -29.25 - 4.60⋅s

Szeregowe połączenie obiekt + regulator PD:

Transmitancja:

Wykres 4. Linie pierwiastkowe - obiekt + regulator idealny PD:

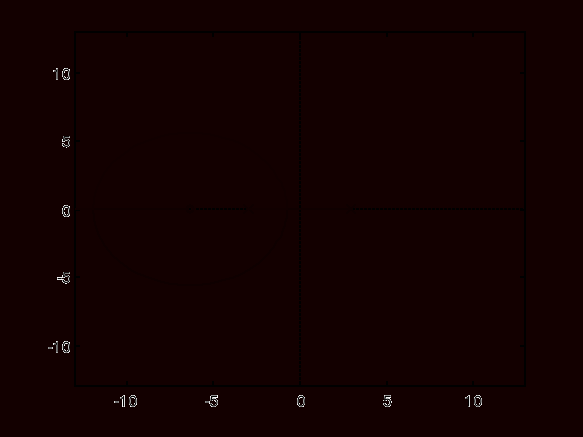
Wykres 5. Odpowiedź układu zamkniętego obiekt + regulator idealny PD na wymuszenie skokowe.

Transmitancja:

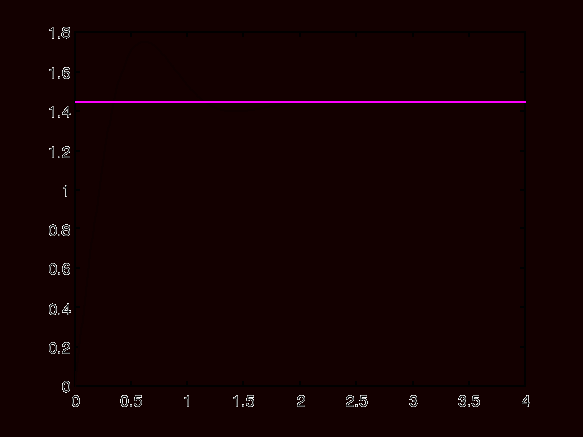
Z wykresu odczytano:

- czas narastania Tr = 0.5s

- przeregulowanie Mp = (ε₂/ε₁)⋅100% = 14,28

- czas ustalania Ts = 2s

Zmiana idealnego regulatora PD na regulator rzeczywisty.

Transmitancja:

Szeregowe połączenie obiekt + regulator rzeczywisty PD (układ otwarty).

Transmitancja:

Wykres 6. Linie pierwiastkowe - obiekt + regulator rzeczywisty PD.

Wykres 7. Charakterystyka skokowa układu zamkniętego z rzeczywistym regulatorem PD (dla K = 1).

Transmitancja:

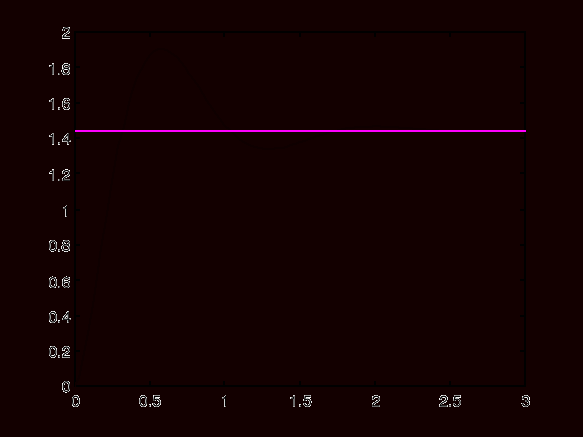
Z wykresu odczytano:

- czas narastania Tr = 0.45s

- przeregulowanie Mp = (ε₂/ε₁)⋅100% = 20

- czas ustalania Ts = 2.5s

Wykres 8. Charakterystyka skokowe układu zamkniętego z rzeczywistym regulatorem PD (dla K = 10).

Transmitancja:

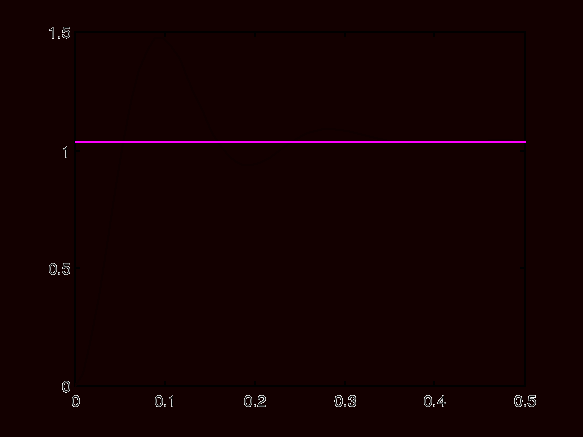
Z wykresu odczytano:

- czas narastania Tr = 0.8s

- przeregulowanie Mp = (ε₂/ε₁)⋅100% = 21,83

- czas ustalania Ts > 0.5s

Wprowadzenie współczynnika całkowania dla idealnego regulatora PID:

G(s) = Kp + Kd⋅s + Ki/s

Dla Ki = 10 otrzymujemy transmitancję:

Układ otwarty: obiekt + regulator idealny PID.

Transmitancja:

Wykres 9. Linie pierwiastkowe - obiekt + idealny regulator PID.

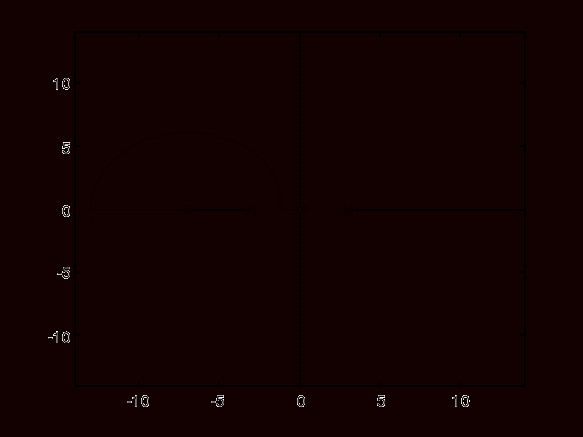
Układ zamknięty: obiekt + regulator idealny PID.

Transmitancja:

Wykres 10. Charakterystyka skokowa układu zamkniętego.

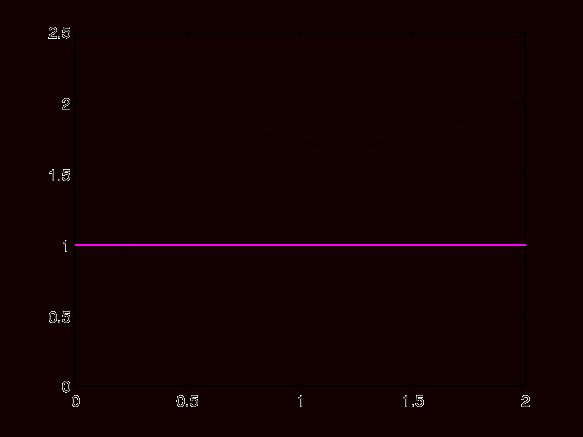
Z wykresu odczytano:

- czas narastania Tr = ∞

- przeregulowanie Mp = ∞

- czas ustalania Ts = ∞

Wprowadzenie współczynnika całkowania dla idealnego regulatora PID:

G(s) = Kp + Kd⋅s + Ki/s

Dla Ki = -10 otrzymujemy transmitancję:

G(s)=
.

Układ otwarty: obiekt + regulator idealny PID.

Transmitancja:

Wykres 11. Linie pierwiastkowe - obiekt + idealny regulator PID.

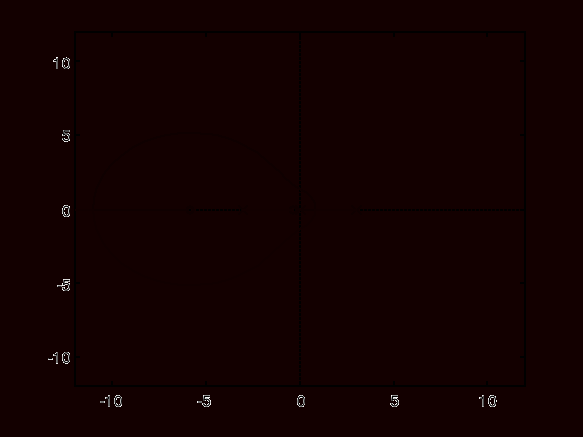
Układ zamknięty: obiekt + regulator idealny PID.

Transmitancja:

Wykres 12. Charakterystyka skokowa układu zamkniętego.

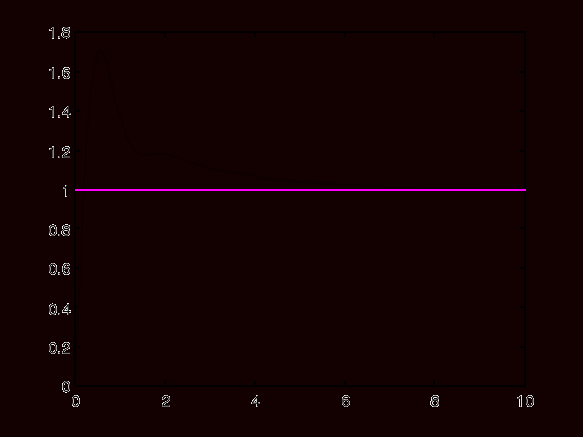
Z wykresu odczytano:

- czas narastania Tr = 0.5s

- przeregulowanie Mp -

- czas ustalania Ts = 8s

5. Wnioski.

Celem ćwiczenia było zapoznanie się z metodą linii pierwiastkowych i wykorzystanie jej do syntezy układu regulacji z niestabilnym obiektem. Ćwiczenie polegało na modelowaniu obiektów regulacji i obserwowaniu wykresów na ekranie monitora. Wszystkie wykonane operacje zostały przeprowadzone na zasadzie symulacji komputerowej. W ćwiczeniu otrzymaliśmy szereg wykresów i transmitancji, w oparciu o które można wysnuć następujące wnioski:

W pierwszej części ćwiczenia obserwowaliśmy zachowanie badanego obiektu współpracującego z „różnymi odmianami” regulatora PD (idealny, rzeczywisty oraz dla różnych wartości współczynnika wzmocnienia K):

- Wykres 1 (linie pierwiastkowe badanego układu).

- Wykres 2 (odpowiedź układu dla parametru K1) - otrzymaliśmy charakterystykę paraboliczną. W oparciu o niego możemy stwierdzić, że dla parametru K1 = -2.5077 układ jest niestabilny i dąży do dużych wartości amplitudy w miarę upływu czasu.

- Wykres 3 (odpowiedź układu dla parametru K2) - otrzymaliśmy charakterystykę sinusoidalną. Układ ze wzmocnieniem K2 = -8.0325 jest lepszy, gdyż oscylacje są stabilne i nie zmieniają się w miarę upływu czasu. Układ znajduje się na granicy stabilności.

- Wykres 4 (linie pierwiastkowe: obiekt + regulator idealny PD) - ponieważ jeden biegun leży po stronie prawej osi urojonej układ jest niestabilny.

- Wykres 5 (odpowiedź skokowa zamkniętego układu: obiekt + regulator idealny PD) - z wykresu odczytano parametry Tr, Mp i Ts. Porównując je z zadanymi parametrami odpowiedzi skokowej możemy stwierdzić jedynie niewielkie różnice spowodowane np.: niedokładnością odczytu czy też przybliżeniami wprowadzanymi przez program symulacyjny.

- Wykres 6 (linie pierwiastkowe: obiektu + rzeczywisty regulator PD) - w układzie tym znów mamy do czynienia z jednym biegunem znajdującym się po prawej stronie osi urojonej, czyli jak już wspomniano układ nie jest stabilny.

- Wykres 7 (charakterystyka skokowa dla układu zamkniętego z rzeczywistym regulatorem PD dla K = 1) - odczytane z wykresu parametry Tr, Mp i Ts w nieznacznym stopniu różnią się od zadanych parametrów odpowiedzi skokowej.

- Wykres 8 (charakterystyka skokowa dla układu zamkniętego z rzeczywistym regulatorem PD dla K = 10) - czas narastania Tr jest tu około dwukrotnie większy od zadanego, natomiast czasu ustalanie nie można dokładnie odczytać, gdyż obserwowany przebieg jest „zbyt krótki”. Oscylacje zaczynają zanikać przy czasie około 0.5s.

W drugiej części ćwiczenia analizowaliśmy zachowanie badanego obiektu współpracującego, tym razem, z „różnymi odmianami” regulatora PDI (idealny dla różnych wartości współczynnika wzmocnienia K):

- Wykres 9 (linie pierwiastkowe: obiekt + idealny regulator PDI dla Ki = 10) - rozkład linii pierwiastkowych dla powyższego układu jest zbliżony kształtem do przypadku: obiekt + regulator idealny PD (Wykres 4) - pojawił się jednak dodatkowy biegun leżący w środku układu współrzędnych. Wynika stąd niestabilność układu.

- Wykres 10 (charakterystyka skokowa układu zamkniętego dla Ki = -10) - jak widzimy badany układ jest układem niestabilnym. Czas narastania Tr, czas regulacji Ts oraz przeregulowanie M_p dążą do ∞.

- Wykres 11 (linie pierwiastkowe: obiekt + idealny regulator PDI dla Ki = -10) - widzimy że, zmiana współczynnika wzmocnienia z Ki = 10 na Ki = -10 spowodowała zmianę kształtu linii pierwiastkowych. Nie zmienił się natomiast rozkład biegunów.

- Wykres 12 (charakterystyka skokowa układu zamkniętego dla Ki = -10) - jak widać, jest ona zdecydowanie różna od charakterystyki poprzedniej (dla Ki =10), a rozpatrywany układ jest stabilny.

W oparciu o wykresy 9 - 12 zauważamy, że poprzez zmianę współczynnika wzmocnienia układu Ki możemy w znaczący sposób wpłynąć na poprawę własności dynamicznych badanego układu.

1

.

---