Rok akademicki 1998/99	Laboratorium z fizyki
Nr ćwiczenia: 71	Promieniowanie cieplne
Wydział: Elektronika Kierunek: T.C.	WALDEMAR PUŁA
Data wykonania	Ocena		Data zaliczenia	Podpis
07-05-99r.	T
	S

1. Zasada pomiaru

Z prawa Kirchoffa wiadomo, że zdolność emisyjna ciał rzeczywistych jest mniejsza niż zdolność emisyjna ciała doskonale czarnego:

R - zdolność emisyjna ciała rzeczywistego

R - zdolność emisyjna ciała doskonale czarnego

a - współczynnik pochłaniania ciała

Z prawa Stefana-Boltzmana wiemy, że zdolność emisyjna ciała doskonale czarnego jest proporcjonalna do czwartej potęgi temperatury:

- stała Stefana-Boltzmana = 5,75 10-8 Wm-2K-4

Emisja energetyczna ciała jest równa mocy wypromieniowywanej przez jednostkę powierzchni ciała R = P/S i po uwzględnieniu powyższych wzorów może być zapisana:

P = a S T4

Jeżeli temperatura otoczenia T_o jest niższa od temperatury ciała T, to wypromieniowywuje ono moc:

P = a S ( T4 - T04)

W doświadczeniu wypromieniowywana moc jest absorbowana przez termoparę i wytwarza w jej obw. prąd elektryczny o mocy P_I proporcjonalnej do mocy P.

Ponieważ : P_I=U2/R ,to P = f U2

Jeśli porównujemy dwa ciała: ciało badane i sadzę (w zakresie promieniowania widzialnego bardzo dobrze symulującą ciało czarne) znajdujące się w tej samej temperaturze zewnętrznej T0, to:

dla ciała badanego:

dla ciała doskonale czarnego:

Ponieważ zarówno powierzchnia obu ciał, jak i temperatury są sobie równe, to po podzieleniu równań stronami otrzymujemy:

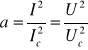
i przystępujemy do wyznaczenia współczynnika pochłaniania ciała badanego.

2. Układ pomiarowy

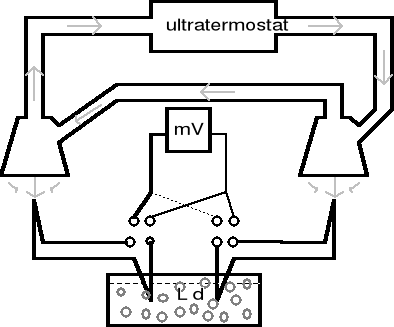
3. Ocena dokładności pojedynczych pomiarów

pomiar temperatury - termometr o dokładności 0,1C - jednak ze względu na to, że pomiar nie był dokonywany bezpośrednio w naczyniach, ale w ultratermostacie, a więc temperatura w czasie obiegu z pewnością spadła to musimy uwzględnić większy błąd pomiaru i przyjęliśmy go:

Δt = 2^oC

Pomiar napięcia - zarówno dla ciała badanego jak i dla sadzy wykonywany tym samym woltomierzem z odczytem cyfrowym - zmiana ostatniej cyfry: 1μV, tak więc ze względu na duże wahania przyjmujemy dokładność :

ΔU = 10 μV

4. Tabela wyników

t	U	Uc	a	/a - ai/
[^oC]	V]	V]	-	-
60	71	135	0,277	0,038
70	90	198	0,207	0,032
80	120	257	0,218	0,021
90	160	317	0,255	0,016
		aśr =	0,239	-
			(a)p.=	0,027

5. Przykładowe obliczenia

pomiar 3: T = 80C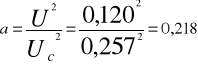

U = 0,120 V Uc= 0,257 V

a_śr = =
= 0,23925 ≈ 0,239

6. Rachunek błędów:

Wybrałem pomiar 3, dla którego będę liczył błąd maksymalny i porównywał go z błędem przeciętnym serii pomiarów.

=

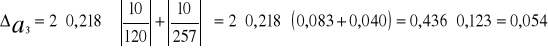
7. Wnioski :

Błąd maksymalny obliczony przy pomocy różniczki logarytmicznej ze wzoru:

jest błędem, wprowadzającym około 18 % błąd, natomiast błąd przeciętny obliczony z poniższego wzoru:

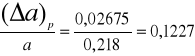
wprowadza błąd o wiele mniejszy bo w granicach 4 %.

Wynik doświadczenia jest zgodny z zasadami teorii promieniowania termicznego, ponieważ zdolność emisyjna ciała rzeczywistego nie może mieć wartości równą jedności, którą posiadają ciała doskonale czarne.

---