Politechnika Śląska

Wydz. Inżynierii Środowiska i Energetyki

Kier. Inżynierii Środowiska

grupa II

WYZNACZANIE STAŁEJ VERDETTA

Sekcja 8

Tomasz Trela

Wstęp teoretyczny

W najczęstszym przypadku światło jest niespolaryzowane tzn. drgania wektorów natężenia pola elektrycznego i wektora natężenia pola magnetycznego odbywają się prostopadle do kierunku rozchodzenia się fali i do siebie nawzajem (parami), lecz we wszystkich możliwych płaszczyznach w których ten kierunek leży. Można uznać w takim przypadku, że światło takie jest złożone z wielu fal o różnych płaszczyznach drgań. Gdy jakiś czynnik zmusi chaotyczne drgania do tego, by odbywały się w jednej płaszczyźnie lub jakiegoś innego obranego porządku, mówimy o polaryzacji światła. Najczęstszym przypadkiem jest polaryzacja liniowa, gdzie drgania już uporządkowane odbywają się ściśle w jednej płaszczyźnie pewnych przypadkach płaszczyzna oscylacji wektora natężenia pola elektrycznego liniowo spolaryzowanego światła obraca się w miarę propagacji fali i obrót ten jest funkcją drogi przebywanej przez światło w danym ośrodku. Mówimy wówczas o zjawisku rotacji optycznej. W zależności od skręcenia płaszczyzny polaryzacji ośrodek może być prawo lub lewo skrętny. Ośrodki w których zjawisko rotacji optycznej zachodzi w warunkach normalnych nazywamy ośrodkami optycznie aktywnymi. Aktywność optyczna danego ośrodka jest związana z ich budową wewnętrzną - np w wodnych roztworach cukru decydujące znaczenie ma kształt cząsteczki cukru. Wyjaśnienie teoretyczne zjawiska rotacji optycznej opiera się na fakcie, że nałożenie na siebie dwóch drgań spolaryzowanych kołowo o przeciwnych zwrotach prowadzi do drgań spolaryzowanych liniowo. Wychodząc z tego założenia przyjmuje się, że światło spolaryzowane liniowo w ośrodku aktywnym optycznie ulega rozkładowi na dwie fale spolaryzowane kołowo: jedną lewoskrętnie i drugą prawoskrętnie oraz fale te propagują w danym ośrodku z różnymi prędkościami. Otrzymujemy następujący związek na zmianę płaszczyzny polaryzacji od przebytej drogi z: =(/) (nl-np) z gdzie:

-kąt skręcenia płaszczyzny polaryzacji

długość danej fali w próżni ,

nl, np -względne współczynniki załamania fal spolaryzowanych lewo i prawo skrętnie w ośrodku optycznie aktywnym, z - przebyta droga. .

Zjawisko aktywności optycznej jest obserwowane także w substancjach po umieszczeniu ich w polu magnetycznym (stają się optycznie aktywne). W przypadku gdy wektor indukcji pola magnetycznego jest skierowany równolegle do kierunku propagacji światła, to efekt tej wymuszonej zewnętrznie rotacji optycznej nosi nazwę zjawiska Faraday'a. Kąt skręcenia płaszczyzny polaryzacji opisuje wówczas empiryczny wzór:

=ρ B w gdzie

B- wektor indukcji pola magnetycznego,

w- droga przebyta przez światło,

ρ- stała proporcjonalności zwana stałą Verdeta.

Wartość stałej Verdeta zależy od: własności substancji, jej temperatury, długości fali.

Opis metody pomiarowej

Wszystkich pomiarów dokonano za pomocą polarymetru. Wykorzystuje on dużą wrażliwość oka ludzkiego na zmianę natężenia oświetlenia

Światło liniowo spolaryzowane pada na przyrząd półcieniowi, który dzieli pole widzenia na części (zaciemnia płaszczyznę polaryzacji w jednej z nich). Za przyrządem 4.2.półcieniowym płaszczyzny polaryzacji tworzą ze sobą niewielki kąt . Dla uzyskania równego oświetlenia analizator ustawia się tak aby jego płaszczyzna polaryzacji dzieliła kąt  na dwie równe części. Po wprowadzeniu ciała optycznie czynnego płaszczyzna polaryzacji światła ulega skręceniu o taki sam kąt i w tym samym kierunku w obydwu częściach pola widzenia. Stąd aby uzyskać równość oświetlenia całego pola widzenia analizator należy skręcić o kąt równy kątowi skręcenia płaszczyzny polaryzacji.

Krótki opis przebiegu ćwiczenia

Ćwiczenie składało się z badania zależność kąta skręcenia płaszczyzny polaryzacji od stężenia roztworu. Dla uzyskania pomiarów przy wyznaczaniu stałej Verdeta zbudowano układ według zamieszczonego poniżej .

W obwodzie jak na schemacie zmieniano natężenie prądu płynącego przez solenoid w zakresie od 14A do 0A co 1A. Przy danym natężeniu prądu dokonywano trzech pomiarów kąta skręcenia płaszczyzny polaryzacji.

Mierzono kąt skręcenia płaszczyzny polaryzacji od stężenia roztworu. Układ stanowiło źródło światła i polarymetr. W czasie ćwiczenia włożono kuwetę, umieszczaną na czas pomiaru wewnątrz polarymetru. Pomiary kąta skręcenia analizatora polarymetru dla danego stężenia powtarzano trzykrotnie. Ogółem wykonano serie pomiarów po 15.

Wyznaczanie stałej Verdeta

1. Łączymy obwód według schematu.

2. Zmieniając natężenie prądu płynącego przez cewkę w zakresie od 14 A do 0 co 1 A mierzymy (trzykrotnie) kąt skręcenia.

3. Rysujemy wykres zależności kata skręcenia płaszczyzny polaryzacji od natężenia prądu:

α = ω ⋅ l ⋅ B = k ⋅ I

gdzie:

• - stała Verdeta badanej cieczy (wodnego roztworu jodku potasu),

• l = 20 cm - długość kuwety,

• k - współczynnik proporcjonalności zależności α = ω ⋅ I,

• B - indukcja magnetyczna

B = μ_o ⋅ b ⋅ n ⋅ I,

μ_o = 4π⋅10^-7 H/m - przenikalność magnetyczna próżni, b = 116 - współczynnik obliczony metodą całkowania graficznego przy uwzględnieniu wymiarów cewki, liczby warstw uzwojenia i grubości drutu nawojowego,

n = 60 m^-1 - liczba zwojów na jednostkę długości cewki

4. Metodą regresji liniowej wyznaczamy współczynnik k, a następnie obliczamy stałą Verdeta:

5. Na wykresie zaznaczamy słupki błędów.

6. Obliczmy błąd wyznaczenia stałej Verdeta.

WYNIKI POMIARÓW I OBLICZENIA

1. Zgodnie z programem ćwiczenia wykonano pomiary kąta skręcenia płaszczyzny polaryzacji w zależności od prądu płynącego w obwodzie. Pomiarów dokonano zmieniając wartość prądu w przedziale 0A do 14A.

I [A]	Kąt skręcenia  [°]
14	11,8
13	10,1
12	10,05
11	9,55
10	8,6
9	7,5
8	6,8
7	6,2
6	5,1
5	4,85
4	4,7
3	3,9
2	1,95
1	1,2
0	0,2

2. Pomiarów dokonano za pomocą miliamperomierza i tak jak w przypadku sprawdzania prawa Malusa wszelkie ewentualne błędy pomiarowe wynikają z dokładności odczytu wartości na skali tego przyrządu.

Dokładność odczytu oraz pozostałe parametry miliamperomierza przedstawiono poniżej:

Dokładność odczytu 50 mA

Klasa przyrządu 0,2 %, zakres 1500 mA

3. Odczyt kąta skręcenia płaszczyzny polaryzacji dokonywany w ćwiczeniu jest obarczony błędem wynikającym z dokładności podziałki noniusza. Błąd ten wynosi:

Błąd pomiaru kąta ±0,05 mm

4. Na podstawie wzoru z programu ćwiczenia

obliczono współczynnik k zależności kąta skręcenia płaszczyzny polaryzacji od prądu fotoelektrycznego. We wzorze tym łatwo zauważyć iż wzór ten jest częścią ogólnego wzoru funkcji liniowej y = a*x + b gdzie:

y = α oraz a = k

Tak więc obliczeń współczynnika można dokonać metodą regresji liniowej co uczyniono korzystając z programu „Analiza” w pracowni laboratoryjnej.

Otrzymane wyniki wraz z błędami ich wyznaczania przedstawiają się następująco:

a = (7,89 ± 0,23)*10^-1-1

b = (5,5 ± 1,0)*10^-1-1

                                                             

Współczynnik korelacji o wartości zbliżonej do jedności świadczy o dużej liniowości tej zależności a co za tym idzie i o tym iż metoda regresji liniowej jest w tym przypadku bardzo dobrym sposobem wyznaczenia współczynnika k, równego współczynnikowi regresji liniowej a.

Współczynnik k wraz z błędem jego wyznaczenia wynosi więc:

Współczynnik k = 7,89 ± 0,23

5. Na podstawie wyliczonego współczynnika k obliczono stałą Verdeta korzystając z zależności:

gdzie:

• ω - stała Verdeta roztworu wodnego jodku potasu

• l = 20 cm = 0,2 m - długość kuwety

• k - współczynnik proporcjonalności [st/A]

• μ_o = 4π⋅10^-7 H/m - przenikalność magnetyczna próżni

• b = 116 - współczynnik obliczony metodą całkowania graficznego przy uwzględnieniu wymiarów cewki, liczby warstw uzwojenia i grubości drutu nawojowego

• n = 60 m^-1 - liczba zwojów na jednostkę długości cewki

Po wstawieniu obliczonego współczynnika k = 7,89 i pozostałych danych otrzymujemy:




6. Następnie obliczono błąd wyznaczenia stałej Verdeta. Do obliczenia tego błędu zastosowano metodę różniczki zupełnej. W tym konkretnym przypadku po przekształceniach wzór na błąd wyznaczenia stałej Verdeta ma postać:

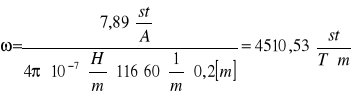
gdzie Δ k błąd wyznaczenia współczynnika k równy 0,018 (regresja liniowa).

Po podstawieniu odpowiednich wartości do wzoru otrzymujemy błąd wyznaczenia stałej Verdeta równy:

Δ = 10,29

Ostatecznie, więc po zaokrągleniu stała Verdeta wraz z błędem jej wyznaczenia wynosi:

Stała Verdeta ω = (4510 ± 10)

WNIOSKI

Dane uzyskane z ćwiczenia posłużyły do wykreślenia zależności kąta skręcenia płaszczyzny polaryzacji od natężenia prądu w solenoidzie. Zależność ta ma charakter liniowy. Seria wyników pomiarowych została aproksymowana prostą, której współczynniki zostały obliczone za pomocą metody regresji liniowej. W wyniku obliczeń otrzymano wartość stałej Verdeta. Wyniosła ona ostatecznie

 = 4510 ± 10


Uzyskany wynik można uważać za dokładny, pamiętając jednak o tym, że przy obliczaniu błędu nie wzięto pod uwagę jak zachowuje się substancja optycznie aktywna w zależności od temperatury. Przez cewkę płynęły duże prądy, które powodowały grzanie się uzwojenia. Nie bez znaczenia jest też czynnik ludzki z subiektywną oceną punktu, w którym występuje równomierne oświetlenie pola widzenia i związany z tym błąd wyznaczenia kąta skręcenia płaszczyzny polaryzacji. Wynik nie jest zadawalający ponieważ policzyliśmy tylko jeden rodzaj skręcenia kąta, ponieważ na więcej nie starczyło czasu.

13

3

---