1. Równowaga względna

Zakładamy że punkt znajduje się w równowadze względem układu ruchomego który porusza się względem innego układu mającego cechy układu Galileusza. Równanie ruchu punktu względem układu ruchomego mp_w=F-mp_u-mp_c w przypadku równowagi w=0 p_w=0 p_c=0 Równanie równowagi względnej F-mp_u=0 Warunkiem równowagi względnej punktu jest równoważenie się układu sił i siły unoszenia punktu.

2.Przyspieszenie Coriolisa

P.C.jest to przyspieszenie wynikające z ruchu unoszenia pc=2ω×w. P.C. jest równe podwojonemu iloczynowi wek-torowemu prędkości kątowej i prędkości względnej, jest prostopadłe do wektorów ω i w pc=2ωwsinϕ gdzie ϕ kąt między wektorami w i ω. Zwrot tego przyspieszenia wynika z przyjętego przez nas zwrotu, określonego przez prawoskrętny prostokątny układ współrzędnych. P.C. jest równe 0 gdy: 1.ruch unoszenia jest postępowy ω=0. 2.w pewnej chwili prędkość względna punktu jest równa 0 w=0, 3.prędkość względna punktu jest równoległa do osi obrotu układu ruchomego sinϕ=0 ωπ=0 (ruch śrubowy). P.C. występuje gdy układ unoszenia dokonuje obrotu.

3.Przyspieszenie unoszenia w ruchu złożonym pkt mat

P.U. jest to przyspieszenie złożone z przyspieszenia punktu ruchomego oraz przyspieszenia obrotowego i dośrodkowego p_u=p_A+p_uo+p_ud= p_A + ε×ρ + ω×(ω×ρ)

4. Równanie dynamiki ruchu względ

Badanie związków między siłami działającymi na punkt materialny a jego ruchem opiera się na II prawie Newtona mp=F. Jednak siła nie musi być stała i może zależeć od czasu położenia i prędkości punktu mp=F(r,v,t) mx''=Fx(x,y,z,x',y',z',t)

5. Uderzenie punktu o przegrodę

Punkt uderza o powierzchnię przegrody będącej w spoczynku z prędkością V₁ której kierunek tworzy kąt α (padania) z normalną powierzchni przegrody. Po uderzeniu punkt odbija się i porusza z prędkością V₂ tworząc kąt β (odbicia) z normalną. W trakcie zderzenia wystąpi reakcja mająca charakter siły zderzeniowej mV₂cosβ+mV₁cosα = J mv2sinβ - mV₁sinα = 0 J-impuls reakcji normalnej. Współczynnik restytucji -stosunek bezwzględnych wartości normalnych składowych prędkości po i przed zderzeniem jest niezależny od prędkości i wymiarów ciał zderzających

6.Współczynnik restytucji.

W.R. jest to stosunek prędkości względnych obu kul po i przed zderzeniem. Prędkości względne mają różne znaki gdyż kule przed zderzeniem się zbliża-ją a po zderzeniu oddalają się od siebie.
,gdzie V₁₁-V₂₁>0

V₁₁ , V₂₁ - prędkość kul przed zderzeniem,

V₁₂ , V₂₂ - prędkość kul po zderzeniu,

7. Wpływ siły impuls na ruch punkt mat

Siła impulsowa powoduje skokową zmianę prędkości zmianę położenia można pominąć

8. Wpływ siły impuls na ciał sztywne.

Skutek uderzenia bryły impulsem siły: skokowy przyrost prędkości środka masy, skokowy przyrost prędkości kątowej

9. Środek uderzenia

Środkiem uderzenia nazywamy pkt. Uderzenia ciała (zadziałania impulsu) w którym to uderzenie nie spowoduje wstrząsu (reakcje=0) ciała.odległóść środka uderzenia od osi obrotu określamy wzorem: z_B= I_x / m z_C

z_B - odl punktu uderzenia os osi obrotu.

I_x - moment bezwładności względem osi obrotu

z_C - odl środka ciężkości od osi obrotu

Uderzenie nie wywoła wstrząsu jeżeli kierunek jego jest prostopadły do płaszczyzny przechodzącej przez oś obrotu i środek masy. Oś obrotu jest osią główną punktu będącego rzutem punktu uderzenia na oś.

10. Zmiana energii kinetycznej pkt materialnego przy uderzeniu o przegrodę.

Punkt uderza w przegrodę prostopadle do jej powierzchni α=β=0
. Różnica energii kinetycznej po i przed zderzeniem wynosi

Następuje więc ubytek energii kinetycznej tym większy im mniejszy jest współczynnik restytucji. W przypadku zderzenia plastycznego cała energia kinetyczna zostaje stracona. W przypadku uderzenia idealnie sprężystego nie ma straty energii. W przypadku częściowo sprężystego zderzenia część energii kinetycznej zostaje stracona, zamienia się w ciepło.

11. Energia kinetyczna ciała sztywnego

12.Twierdzenie Koeniga.

E.K. ciała sztywnego równa jest sumie E.K. ruchu postępowego z prędkością środka masy i energii ruchu obrotowe-go wokół osi przechodzącej przez środek masy.

V_A -prędkość dowolnego pktu A

V_AX , V_AY , V_AZ -rzuty wektora V na osie

X_C , Y_C , Z_C - wsp. środka masy w ruchomym ukł. bezwł.

13. Niewyrównoważanie statyczne i dynamiczne ciała sztywnego

Niewyrównoważanie statyczne zachodzi wtedy gdy środek ciężkości nie pokrywa się ze środkiem obrotu ciała.

Niewyrównoważanie dynamiczne zachodzi wtedy gdy oś obrotu nie jest osią główną w żadnym swoim punkcie.

14.Reakcje dynamiczne w łożyskach wirującej bryły

Jeżeli środek masy ciała leży na osi obrotu i jednocześnie oś ta jest osią główną ciała dla dowolnego jej punktu to reakcje dynamiczne są równe 0. Reakcje dynamiczne występują jeżeli środek masy ciała wirującego nie leży na osi obrotu oraz jeżeli oś ta nie jest osią główną. Do reakcji statycznych wynikających z obciążenia siłami dochodzą reakcje dynamiczne konieczne do utrzymania ciała w określonym ruchu obrotowym. Reakcje te wynikają ze zmian pędu i krę tu ciała. Gdy oś obrotu nie przechodzi przez środek masy ciała występuje okresowa okresowa zmiana siły działającej na łożyska. Siła ta przenosząc się na elementy fundamentu wywołuje drgania.

Obl. Reakcji :

Niewyrównoważenie statyczne:

Niewyrównoważenie dynamiczne

15. Zjawisko żyroskopowe - istota, zastosowanie.

Moment żyroskopowy wyraża opór z jakim w skutek swej bezwładności wirujące ciało przeciwstawia się zmianie osi obrotu. Żyroskop wykorzystywany jest jako wskaźnik położenia i zmian kierunku ruchu, a także w wirnikach, śmigłach, wałkach silników, wywieranie reakcji żyroskopowych podczas zmiany ruchu kierunków pojazdu.

16.Równanie ruchu punktu o zmiennej masie.

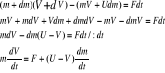
v-prędkość punktu u-prędkość dołączającej się cząstki

17.Kiedy równanie ruch pkt materialnego o zmiennej masie ma postać II prawa Newton

Gdy prędkość względna dołączającej się masy jest równa zero w=U-V=0

Wtedy
, z tym że m=m(t) - f. czasu

Równanie ma formalnie postać identyczną z równaniem ruchu punktu o stałej masie, z tym że masa jest funkcją czasu.

18.Kiedy równanie Mieszczerskiego

Gdy prędkość bezwzględna dołączającej się masy jest równa 0. Otrzymujemy
, więc

19.Praca przygotowana

Przesunięciem przygotowanym nazywamy takie dowolnie pomyślane przez obserwatora przesunięcie będące jednym z przesunięć możliwych nie związane ani z działającymi siłami ani z czasem. Jeżeli na punkt materialny działa siła F_i to po nadaniu punktom przesunięcia przygotowanego δr_i zostanie wykonana praca elementarna δL_i = F_i ⋅ δr_i Pracę elementarną siły na przesunięciu przygotowanym nazywamy pracą przygotowaną. W położeniu równowagi układu , suma prac przygotowanych wszystkich sił zew. i reakcji jest równa 0.

Zasadę prac przygotowanych stosuje się przy ukł. statycznie nie wyznaczalnych.

20. Określenie współ rzędnych uogólnionych i sił uogólnionych dla układu punktów materialnych.

Niezależne współ, których liczba jest najmniejszą potrzebną do określenia położenia układu nazywamy współ uogól.

x_i = x_i(..., q_j ,...) i = 1,..., n

y_i = y_i(..., q_j ,...) j = 1,..., s

z_i = z_i(..., q_j ,...) s - l. st. swobody

siłą uogólnioną nazywamy taką wielkość, która pomnożona przez przyrost przygotowany δ_g współ uogólnionej daje wartość pracy wykonanej przez układ sił działających na dany układ materialny na przesunięciach przygotowanych, wywołanych przyrostem współ uogólnionej.

20. Współrzędne i siły uogólnione

Niezależne współrzędne których licz-ba jest najmniejszą potrzebną do określenia położenia układu nazywamy współrzędnymi uogólnionymi. Mogą być dowolnymi współrzędnymi liniowymi lub kątowymi. Siłą uogólnioną nazywamy taką wielkość która pomnożona przez przyrost przygotowany δqj współrzędnej uogólnionej daje wartość pracy wykonanej przez układ sił działających na dany układ materialny na przesunięciach przygotowanych wywołanych przyrostem współrzędnej uogólnionej. Qj=δLj/δqj.

21. Zasada d'Alemberta.

Suma iloczynów skalarnych sum sił zewnętrznych i wewnętrznych działających na punkty układu oraz wektorów (-m_ip_i) i przesunięć przygotowanych punktów układu materialnego jest równa 0. ∑(F_i+W_i-m_ip_i)⋅δr_i=0. Do badania ruchu układu swobodnego pod działaniem sił zewnętrznych może być zastosowana zasada: Układ sił zewnętrznych działających na punkty układu materialnego swobodnego równo-waży się w każdej chwili z układem sił bezwładności S+S_B=0 M_O+M_BO=0 Dla układu nieswobodnego: Układ wektorów złożony z sił bezwładności układu materialnego sił zewnętrznych działających na ten układ oraz z sił reakcji ograniczających ruchy tego układu jest układem równoważnym 0.

Zasada d'Alemberta ma zastosowanie przy konstrukcji równań ruchu układów materialnych.

22. Określenie przemieszczenia wirtualnego (przygotowanego)

Przesunięciem przygotowanym nazywamy takie dowolne przesunięcie pomyślane przez obserwatora będące jednym z przesunięć możliwych, nie związane ani z działającymi siłami ani z czasem.

23.Zderzenia proste, centralne

Przy zderzeniu dwóch ciał powierzchnie tych ciał zetkną się w jednym punkcie. Punkt A I ciała zetknął się z punktem D II ciała. Powierzchnie tych ciał w punkcie zetknięcia mają wspólną normalną (linia zderzenia). Prędkość względna punktu A w stosunku do punktu D jest równa i przeciwna prędkości względnej punktu D w stosunku do punktu A. Jeżeli te prędkości względne są położone na linii zderzenia to zderzenie nazywamy prostym w przeciwnym razie ukośnym. Przy zderzeniu prostym siły chwilowe działają na linii zderzenia. Jeżeli linia zderzenia przechodzi przez środek masy ciała to zderzenie nazywamy centralnym w odróżnieniu od zderzenia mimośrodowego w przypadku przeciwnym.

24. Zderzenie dwóch kul.

Zakładamy że dwie kule o masach m₁ i m₂ poruszają się ruchem postępowym z prędkościami V₁₁ i V₁₂ przed zderzeniem tak że torem środka masy każdej z nich jest prosta na której znajdują się ich środki O1 i O2. Aby zderzenie było możliwe V₁₁-V₁₂> 0. Rzut wektora pędu na oś x wobec braku sił zewnętrznych jest stały. Po uderzeniu kule zaczną poruszać się z prędkościami V₁₂ i V₂₂ skierowanymi także wzdłuż osi x. Stałość pędu oznacza że pęd układu po i przed zderzeniem jest taki sam m₁V₁₂+m₂V₂₂=m₁V₁₁+m₂V₂₁ Stosunek prędkości względnych obu kul po i przed zderzeniem jest równy współczynnikowi restytucji k=v12-v22/v11-v21 Przy zderzeniu plastycznym k=0 przy idealnie sprężystym k=1.

25. Ruch kulisty precesja regularna

Ruch kulisty bryły-występuje wtedy ,gdy jeden z pktów układu związanego z ciałem jest nieruchomy . Ruch ten jest

ruchem o 3 stopniach swobody.
gdzie A- pkt nieruchomy.

Precesja regularna jest to szczególny przypadek ruchu kulistego ciała w którym prędkości kątowe obrotu własnego i precesji są stałe ϕ'=ω1=const ψ'=ω2=const a prędkość kątowa nutacji jest równa 0 więc kąt nutacji jest stały ϑ'=0 ϑ=ϑ0=const Ruch ten cechuje się tym że ciało obraca się wokół osi własnej ζ z prędkością kątową ω1 a oś ta obraca się wokół osi stałej z z prędkością kątową ω2. Kąt między osiami jest stały. Stałe prędkości oznaczają że kąty ψ i ϕ zmieniają się w sposób jednostajny. Ruch opisany jest równaniami ruchu ϕ=ω1t ψ=ω2t ϑ=ϑ0 przy założeniu że w chwili początkowej t=0 kąty ϕ i ψ są równe 0 ω=ω1+ω2

26. Pręt o masie m i dł. l porusza się po płaszczyźnie tak że prędkość jego końców wynoszą V₁ i V₂ i są prostopad do pręta. Jaka jest energia kinetyczna pręta?

27. Równanie ruchu rakiety

Ruch rakiety w czasie działania silnika rakietowego jest ruchem ciała o zmiennej masie podczas którego następuje wypływ gazów spalinowych z dyszy silnika z prędkością względną uzyskiwaną w wyniku spalania paliwa. Zakładamy że prędkość względna gazów jest styczna do trajektorii oraz prędkość względna gazów jest stała w = u - v = -wτ τ-wektor jednostkowy styczny do trajektorii.

V(0) = V₀ m(0) = m₀

-równanie ruchu rakiety.

28.Równania ruchu ciała sztywnego

R.r.c.s. otrzymamy jako szczególny przypadek równań ruchu układu materialnego. Możemy je otrzymać za pomocą zasady pędu i krętu. Pochodna pędu względem czasu równa jest wektorowi głównemu sił zewnętrznych i reakcji a pochodna krętu względem nieruchomego punktu momentowi głównemu sił zewnętrznych i reakcji. B'=S K'_o=M_o

B'_x=S_x ...K'_x=M_x...

B'_y=S_y K'_y=M_y

B'_z=S_z K'_z=M_z

S_x,S_Y,S_Z-rzuty wektora głównego sił zew. i reakcji

M_x,....-rzuty momentu głównego

Równanie w ukł. ruchomym ξ ,ζ , η

B' + ω B - ω B = S

B' + ω B - ω B = S

B' + ω B - ω B = S

K +

K +

K +

29. Równania Lagrange'a II rodzaj

d/dt⋅∂E/∂q'j-∂E/∂qj=Qj j=1,2,...,s

Są to równania różniczkowe zwyczajne II rzędu. Rozwiązanie tych równań stanowi najkrótszy sposób badania ruchu. Liczba równań różniczkowych jest przy tej metodzie najmniejsza i rów-na liczbie stopni swobody układu. W równaniach tych występuje s niewiadomych przedstawiających s współrzędnych uogólnionych określających ruch układu. Równania te nie zawierają reakcji toteż nie pozwalają one na wyznaczenie wartości tych reakcji

30.Równania Lagrange'a potencjal

W przypadku gdy siły zewnętrzne działające na układ mają potencjał siłę uogólnioną można obliczyć jako pochodną potencjału względem odpowiedniej współrzędnej Qj=-∂V/∂qj wtedy równania Lagrange'a d/dt(∂E/∂q'j)-∂E/∂qj+∂V/∂qj=0 Potencjał kinetyczny L=E-V jest to różnica energii kinetycznej i potencjału sił. Ponieważ potencjał nie zależy od prędkości uogólnionej d/dt(∂L/∂q'j)-∂L/∂qj=0 Potencjał kinetyczny przedstawia nadmiar energii kinetycznej nad potencjalną.

31. Dysypacyjna funkcja Rayleigha i jej zastosowanie

F = -cv -opory wishotyczne

D = D(q,.. q_s, q,.. q_s)

32. Rów dynamiki toczącego koła

Ruch taki wykonują koła pojazdu jeże-li pudło pojazdu wykonuje ruch postępowy po linii prostej. Przy takim ruchu koło toczy się po jezdni obracając się jednocześnie. Koło obciążone jest siłami przekazanymi przez oś na której zostało osadzone oraz reakcjami prostej (jezdni) i własną siłą ciężkości. Przyjmujemy że siły obciążające koło przekazane przez oś z uwzględnieniem własnego ciężaru sprowadzają się do dwóch składowych pionowej P i poziomej F oraz pary sił o momencie M. Siły te przyłożone są w punkcie C. Zakładamy że punkt ten pokrywa się ze środkiem masy koła. Ze strony toru (jezdni) działa na koło reakcja normalna N i siła tarcia T. Reakcja normalna ze względu na opór toczny przesunięta jest o f w kierunku ruchu a siła tarcia skierowana w dodatnią stronę osi x gdyż przeciwstawia się poślizgowi koła po szynie przy wskazanym kierunku działania momentu M. Jeżeli koło toczy się bez poślizgu to między prędkością środka masy C a prędkością kątową istnieje związek rω-vc=0 czyli ω=vc/r Równania ruchu są następujące mv'c=F+T 0=N-P Iω'=M-Nf-Tr

34.Wyprowadzić wyrażenia na współ wektora krętu ciała sztywnego względem punkturuchomego
Współrzędne krętu:

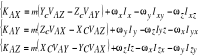
36.Prawo ruchu środka masy

Środek masy układu materialnego porusza się tak jak punkt materialny w którym skupiona jest masa całego ciała i do której przyłożone są siły równe wektorom głównym sił zewnętrznych i reakcji działających na dany układ. mpc=S+R mx''c=∑Fix+∑Rix ...

37. Prawo zmienności pędu i krętu.

Pochodna wektora pędu układu materialnego względem czasu równa jest sumie geometrycznej sił zewnętrznych i reakcji działających na układ dB/dt=∑(F_i+R_i). Pochodna względem czasu krętu układu materialnego względem dowolnego stałego punktu rów-na jest sumie momentu głównego sił zewnętrznych i momentu głównego reakcji względem tego samego punktu. dK_o/dt=M_o+H_o

38. Prawo zmienności energii układu punktów materialnych w potencjalnym polu sił

Przyrost elementarnej energii kinetycznej układu materialnego równy jest sumie prac elementarnych sił zew., wew. i reakcji:

39. Współrzędne wektora krętu

40. Równa dynam ruchu postępowego bryły

W ruchu postępowym ciała sztywnego swobodnego liczba równań ruchu wynosi 3. Najkorzystniej obrać równania wynikające z prawa zmienności pędu. Ponieważ w ruchu postępowym ω=0 nie ma prawa zmienności krętu dB/dt=∑(Fi+Ri) m⋅dvc/dt=∑(Fi+Ri) mx''c=∑(Fix+Rix) my''c=∑(Fiy+Riy)

41. Równanie ruchu obrotowego bryły.

Ruch obrotowy ciała sztywnego dokoła osi stałej jest ruchem o jednym sto-pniu swobody. Ruch ciała określa się jednym równaniem ruchu podającym zależność kąta obrotu od czasu. Najkorzystniej jest jako równanie to przyjąć jedno z równań krętu d/dt⋅(I⋅ω)=Ml lub Il⋅ε=Ml Il-moment bezwładności względem osi obrotu Ml-moment sił zewnętrznych i reakcji względem osi obrotu

42.Uproszczona teoria precesji regularnej

Zakładamy że ciało ma oś symetrii i że środek ruchu kulistego O leży na tej osi. Zakładamy że ciało obraca się wokół osi symetrii ze stałą prędkością kątową ω₁, a jednocześnie oś ta obraca się wokół innej osi nieruchomej przyciągającej się z osią obrotu własnego w punkcie O ze stałą ω₂. Ruch taki nazywa się precesją regularną

43. Opisz znane ci zasady mechaniki analitycznej

1. Zasada prac przygotowanych umożliwia nam rozwiązywanie układów statycznie niewyznaczalnych. Polega ona na tym że układamy równania prac przygotowanych (sił układu działających na przesunięciach przygotowanych). Z równań tych możemy wyznaczyć wartości tych sił lub zależności między nimi:

2. Zasada d'Alemberta ma zastosowanie przy konstrukcji równań ruchu. Polega ona na tym iż układamy równanie prac przygotowanych sił działających na układ oraz sił bezwładności:

3. Równania Lagrange'a są dynamicznymi równaniami równowagi układów mechanicznych. Rozróżniamy równanie „sił uogólnionych”, w polu potencjalnym, służą nam one do badania ruchu układu materialnego:

44.Prawo zmienności pędu ciała szt

Pęd ciała sztywnego równy jest iloczynowi masy ciała i prędkości środka masy B=mvc Dla ciała sztywnego jako dla układu materialnego słuszne jest prawo zmienności pędu: Pochodna wektora pędu układu materialnego względem czasu równa jest sumie geometrycznej sił zewnętrznych i reakcji działających na układ dB/dt=∑Fi+∑Ri

45.Prawo zmien krętu ciała sztywn

Ko=rA×B+KA Ko-kręt ciała względem nieruchomego punktu KA-kręt ciała względem punktu ruchomego B-pęd Dla ciała sztywnego jako dla układu materialnego słuszne jest prawo zmienności krętu: Pochodna względem czasu krętu układu materialnego względem dowolnego stałego punktu rów-na jest sumie momentu głównego sił zewnętrznych i momentu głównego reakcji względem tego samego punktu dKo/dt=Mo+Ho

48. Pojęcie więzów ukł. mech. i ich klasyfikacja.

Układ którego punkty nie mogą zajmować dowolnych położeń i mieć dowolnych prędkości niezależnie od działających sił nazywamy nieswobodnym. Na położenie i prędkości wszystkich lub niektórych punktów układu nałożone są warunki ograniczające ich swobodę zwane więzami. Więzy określ-one równaniami nazywają się więzami dwustronnymi, nierównościami jedno-stronnymi. Jeżeli równanie więzów zawiera tylko współrzędne punktów to nazywamy je więzami geometryczny-mi. Równania więzów mogą być także zależne od prędkości punktów (więzy kinematyczne). Oba rodzaje więzów mogą być ponadto zależne od czasu (więzy niestacjonarne). Więzy nie-zależne od czasu- więzy stacjonarne.

względnej punktu jest równoważenie się układu sił i siły unoszenia punktu.

punkcie C. Zakładamy że punkt ten pokrywa się ze środkiem masy koła. Ze strony toru (jezdni) działa na koło reakcja normalna N i siła tarcia T. Reakcja normalna ze względu na opór toczny przesunięta jest o f w kierunku ruchu a siła tarcia skierowana w dodatnią stronę osi x gdyż przeciwstawia się poślizgowi koła po szynie przy wskazanym kierunku działania momentu M. Jeżeli koło toczy się bez poślizgu to między prędkością środka masy C a prędkością kątową istnieje związek rω-vc=0 czyli ω=vc/r Równania ruchu są następujące mv'c=F+T 0=N-P Iω'=M-Nf-Tr

50. wyznaczanie siły uogólnionej odpowiadającej danej współrzędnej uogól równania Lagrange'a( przykład)

δL = ....(...)δq₁ + ...+(...)δq_s

Q₁ Q_s

Aby wyznaczyć siły uogólnione odpowiadające współrzędnym:q₁,...,q_s piszemy wyrażenie na pracę przygotowaną sił działających na układ

Q₁ i Q_s podstawiamy do odpowiednich równań Lagrang

1 Równowaga względna

2 Przyspieszenie Coriolisa

3,4 Przys unoszenia w ruch złoż

4 Równ dynam ruchu względn

5 Uderzenie punktu o przegrodę

6,7,8 Współczynnik restytucji

7 Wpływ siły impuls na ruch pkt

8 Wpływ siły impuls na ciał sztywn

10,12 Zmian Ek przy ud o przeg

12 Twierdzenie Koeniga

14 Reak dynam w łożyskach

16,17,18 Rów ruch pkt o zmien masie

17 Kiedy równ ma II Newtona

18 Kiedy równ Mieszczerskiego

19 Zasada prac przygotowanych

21 Zasada d'Alemberta

23 Określenie zderzenia

24 Zderzenie dwóch kul

25 Ruch kulisty precesja

27 Równanie rakiety

28 Równ ciała sztywnego

29 Równ Lagrange'a II

30 Równ Lagrange'a potenc

34,36 Współrz krętu ci szt pkt ruch

36 Prawo ruchu środka masy

37 Prawo zm pędu i krętu ukł

40 Równa dynam ruchu postępow

41 Równ ruchu obrot bryły

44.Prawo zmienności pędu ciała szt

45.Prawo zmien krętu ciała sztywn

48 Pojęcie więzów

---