Przedziały ufności dla średniej
Model I
Populacja generalna ma rozkład N (m, σ), m - nieznane, σ - znane.
Z populacji pobrano próbkę n-elementową. Przedział ufności dla średniej m wynosi:
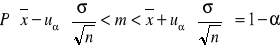
![]()
- średnia arytmetyczna z wyników próby.
uα - wyznacza się z rozkładu normalnego
Model II
Populacja generalna ma rozkład N (m, σ), m - nieznane, σ - nieznane.
Z populacji pobrano małą próbkę n-elementową. Przedział ufności dla średniej m wynosi:
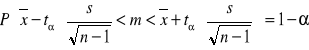
lub 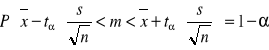
![]()
,
![]()
- średnia arytmetyczna z wyników próby.
tα - wyznacza się z rozkładu t Studenta
Model III
Populacja generalna ma rozkład N (m, σ), bądź dowolny inny rozkład o średniej m i skończonej wariancji σ2 - nieznanej.
Z populacji pobrano dużą próbkę n-elementową (co najmniej kilkadziesiąt). Przedział ufności dla średniej m wynosi:
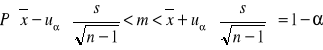
lub 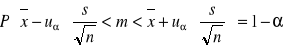
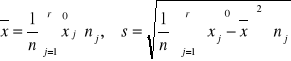
,
![]()
- środek poszczególnego przedziału klasowego,
nj - liczebność przedziału klasowego,
r - liczba przedziałów klasowych.
Jeżeli liczba przedziałów klasowych r jest mała i długość h każdego przedziału klasowego jest duża, obliczając wartość s należy stosować tzw. poprawkę na grupowanie czyli odjąć od s2 wartość 1/12h2 a dopiero potem wyciągnąć pierwiastek.
Przedział ufności dla wskaźnika struktury (procentu)
Model
Populacja generalna ma rozkład dwupunktowy z parametrem p, p >0,05. Wylosowano dużą próbę n > 100. Przedział ufności dla wskaźnika struktury p:
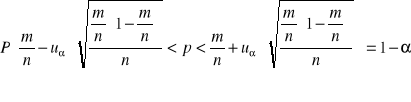
Przedział ufności dla wariancji
Model I
Populacja generalna ma rozkład N (m, σ), m - nieznane, σ - nieznane.
Z populacji pobrano próbkę n-elementową (n<30). Z próby oblicza się s2 lub ![]()
. Przedział ufności dla wariancji σ2 wynosi:
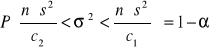
lub 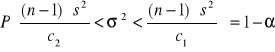
![]()
c1, c2 - wartości zmiennej ![]()
z tablicy rozkładu χ (n-1; 1-α).
c1 dla (1 - 1/2α),
c2 dla 1/2α
Model II
Populacja generalna ma rozkład N (m, σ) lub zbliżony do normalnego, m - nieznane, σ - nieznane. Z populacji pobrano dużą próbkę n-elementową. Z próby oblicza się s2 lub ![]()
. Przedział ufności dla odchylenia standardowego σ wynosi:
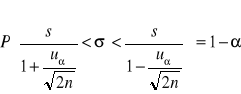
Zad. 1.
Wytrzymałość pewnego materiału budowlanego jest zmienną losową o rozkładzie normalnym N (m, σ). W celu oszacowania nieznanej średniej m wytrzymałości tego materiału dokonano pomiarów wytrzymałości na n = 5 wylosowanych niezależnie sztukach tego materiału. Wyniki pomiarów były następujące: (w kG/cm2): 20,4 19,6 22,1 20,/8 21,1. Przyjmując współczynnik ufności 1 - α = 0,99 zbudować przedział ufności dla średniej wytrzymałości m tego materiału.
Zad. 2.
Chcemy oszacować średni staż pracy pracowników pewnego zakładu. W tym celu z populacji pracowników wylosowana została próba n=100 osób i otrzymano następujące wyniki (pogrupowane w szereg rozdzielczy):
Staż pracy w latach xj |
Liczba pracowników nj |
0 - 2 |
4 |
2 - 4 |
10 |
4 - 6 |
55 |
6 - 8 |
25 |
8 - 10 |
6 |
Przyjmując współczynnik ufności 1 - α = 0,90, zbudować przedział ufności dla średniego stażu pracy badanej populacji pracowników.
Zad. 3.
W pewnym eksperymencie chemicznym badano czas przebiegu pewnej reakcji. Dokonano
n = 60 niezależnych doświadczeń i otrzymano z nich średnią xsr = 46 sekund i odchylenie standardowe s = 13 sek. Przyjmując współczynnik ufności 0,99 oszacować metodą przedziałową średni czas potrzeby na przebieg na przebieg tej reakcji.
Zad. 4.
Dokonano n = 7 pomiarów ciśnienia w komorze spalania silnika i otrzymano następujące wyniki (w kG/cm2): 31,85 31,36 30,32 30,90 31,70 32,40 31,60.Ciśnienie to ma rozkład normalny. Metodą przedziałową oszacować średnie ciśnienie w komorze spalania tego silnika przyjmując współczynnik ufności 1 - α = 0,99.
Zad. 5.
W celu oszacowania średniej powierzchni wybudowanych w 1996 roku w Krakowie mieszkań wylosowano niezależnie 120 wybudowanych w tym roku mieszkań i otrzymano dla nich następujący rozkład powierzchni mieszkalnej (w m2):
Powierzchnia mieszkalna |
Liczba mieszkań |
15 - 25 |
10 |
25 - 35 |
25 |
35 - 45 |
40 |
45 - 55 |
30 |
55 - 56 |
10 |
65 - 75 |
5 |
Zbudować przedział ufności dla średniej powierzchni mieszkań, przyjmując 1 - α = 0,90
Zad. 6.
Oszacować jaki procent studentów jada obiady w stołówkach. Pobrano w tym celu próbkę n = 900 osób i znaleziono w tej próbce m = 300 osób, które jedzą obiady w stołówkach. Dla współczynnika ufności 1 - α = 0,95 zbudować przedział ufności dla procentu badanej kategorii.
Zad. 7.
Badając wytrzymałość pewnego materiału dokonano n = 4 niezależnych pomiarów i otrzymano wyniki (w kG/cm2): 120, 102, 135, 115. Zbudować przedział ufności dla wariancji σ2 dla 1 - α = 0, 94.
Zad. 8.
W badaniach budżetów rodzinnych zbadano 632 gospodarstwa domowe i otrzymano dane: średnia miesięczna wydatków wyniosła 1570 zł, odchylenie standardowe 224 zł. Dla współczynnika ufności 1 - α = 0,90 zbudować przedział ufności dla odchylenia standardowego wydatków.
Wyznaczanie niezbędnej liczby pomiarów
Model I
Populacja generalna ma rozkład N (m, σ), σ2 - znane. Chcemy oszacować średnią wartość populacji m na podstawie próby złożonej z n niezależnych elementów. Niezbędną liczebność próby n oblicza się ze wzoru:
![]()
uα, - wartość zmiennej normalnej N(0,1) dla 1 - α;
d - maksymalny ustalony błąd szacunku.
Model II
Populacja generalna ma rozkład N (m, σ), σ2 - nieznane, ![]()
- znane, mała liczba elementów. Niezbędną liczebność próby n oblicza się ze wzoru:
![]()
,
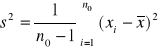
,
n0 - liczebność małej próby,
tα - wartość statystyki t-Studenta
Model III
Populacja generalna ma rozkład dwupunktowy z parametrem p. Jeżeli znamy spodziewany rząd wielkości p, to wielkość próby ustala się wg wzoru:
![]()
p - spodziewany rząd wielkości szacowanego wskaźnika struktury; q = 1 - p.
Jeżeli nie znamy rzędu wielkości szacowanego wskaźnika struktury p, to przyjmujemy, że pq=1/4 i otrzymujemy wzór:
![]()
Zad. 1.
Zbadać ile niezależnych obserwacji powinna liczyć próba, by na jej podstawie można było oszacować średni czas mielenia rudy piaskowcowej w młynie prętowym z błędem maksymalnym 20 minut, współczynnik ufności 0,95. Czas mielenia jest zmienną losową N(m, 40).
Zad. 2.
Oszacować średnią zawartość miedzi w rudzie piaskowcowej. Ile próbek należy pobrać aby przy wsp. ufności 0,95 oszacować tę zawartość metodą przedziałową z błędem maksymalnym 0,01 %Cu, jeżeli próba wstępna 5 niezależnych pomiarów dała następujące wyniki (w % Cu): 2,10 2,12 2,12 2,16 2,10
Zad. 3.
Ile należy wylosować studentów AGH aby oszacować procent palących z błędem maks. 5% i współczynniku ufności 0,90. Szacowany procent palących jest rzędu 70%.
Zad. 4.
Ile należy wylosować puszek konserw do badania, aby oszacować procent zepsutych konserw, który jest przypuszczalnie rzędu 10%, z błędem maks. 5%, współczynnik ufności 0,90.
Zad. 5.
Ilu pacjentów szpitala należy wylosować aby z błędem maks. 10 dni oszacować średni czas przebywania ich w szpitalu, jeżeli próba 15 wylosowanych pacjentów dała następujące czasy przebywania w szpitalu w dniach: 206 184 272 240 225 196 257 217 236 208 190 248 233 260 188. Współczynnik ufności 0,90.
Testy parametryczne (wzory)
Test dla wartości średniej
Model I: ![]()
Model II: ![]()
Model III: ![]()
Test dla dwóch średnich
Model I: 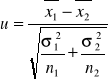
Model II: 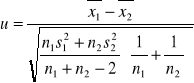
Model III: 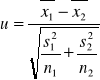
Test dla wskaźnika struktury
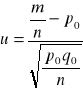
Test dla wariancji
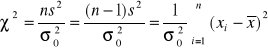
Test zgodności χ2
H0: F(x) ∈ Ω
Populacja ma rozkład ciągły o dystrybuancie o określonym typie funkcyjnym
duża próbka (co najmniej kilkadziesiąt)
wyniki dzielone są na r klas o liczebności ni każda (
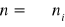
)powstaje hipotetyczny rozkład Ω
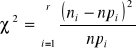
ni - liczebność i-tej klasy
pi - prawdopodobieństwo, że zmienna losowa przyjmuje wartości z i-tej klasy w rozkładzie Ω
r - liczba klas
![]()
χ2 < χ2teoret nie ma podstaw do odrzucenia H0
χ2 ≥ χ2teoret H0 odrzucamy
Test zgodności λ Kołmogorowa
H0: F(x) = F0(x), F0 - hipotetyczna ciągła dystrybuanta
populacja ma rozkład ciągły o dystrybuancie F(x)
duża próbka (co najmniej kilkadziesiąt)
wyniki są porządkowane w kolejności rosnącej lub w klasach (wąskie przedziały) o liczebnościach ni
dla każdego xi (prawa strona przedziału) wyznacza się wartość empirycznej dystrybuanty Fn(x) ze wzoru:
![]()
nsk - skumulowana liczebność od początku do danej klasy
korzystając z rozkładu normalnego obliczana jest wartość hipotetycznej dystrybuanty F(x)
D = sup | Fn(x) - F(x) |
λ = D ![]()
λteoret (α)
λ < λteoret nie ma podstaw do odrzucenia H0
λ ≥ λteoret H0 odrzucamy
7
Wyszukiwarka
Podobne podstrony:
Gubin parametry, AGH, Semestr X, stateczność skarp i zboczy, Stateczność skarp TOEZ
Materiaoznawstwo - opracowany egzamin (termin o), AGH, 5 semestr, material
Inzynieria materialowa czesc obliczeniowa, Elektrotechnika AGH, Semestr III zimowy 2013-2014, Inżyni
sciaga statystyka, Politechnika Poznańska, Magisterka ZIiP, Semestr I (VIII), Statystyka
stataystyka, Politechnika Poznańska, Magisterka ZIiP, Semestr I (VIII), Statystyka
Gubin parametry, AGH, Semestr X, stateczność skarp i zboczy, Stateczność skarp TOEZ
Estymacja przedziałowa parametrów
ESTYMACJA STATYSTYCZNA duża próba i analiza struktury, Semestr II, Statystyka matematyczna
kolokwium 1 2012, ZiIP - GIG AGH, Semestr 3, Statystyka
ESTYMACJA STATYSTYCZNA2 duża próba i analiza struktury(2), Semestr II, Statystyka matematyczna
Cwicz1, Skrypty, UR - materiały ze studiów, studia, studia, Bastek, Studia, Rok 4, Semestr VIII, Bud
Rys 2c, AGH, Semestr 10, Zmenczenie materialow pod kontrola, Sprawozdanie I
Filozofia karta przedm, semestr VIII, Semestr VIII, VIII semestr, Filozofia, Materiały od wykładowcy
podkład, Skrypty, UR - materiały ze studiów, studia, studia, Bastek, Studia, Rok 4, Semestr VIII, Ks
PNOM - metale, AGH, Semestr II, Podstawy Nauk o materiałach[Kot,Dymek,Rakowski], PNOM, PNOM
03 Statystyka Matematyczna Estymacja przedziałowaid 4487
więcej podobnych podstron