Statystyka to dyscyplina nauki zajmująca się
metodami zbierania,
opracowywania i analizy danych o zjawiskach
masowych
Celem jest:
*znalezienie prawidłowości kształtujących zjawiska:
- badanie struktury
kosztów produkcji
- badanie zmian w
poziomie i strukturze ludności na określonej przestrzeni i czasie
- badanie związku
pomiędzy stażem pracy a wydajnością pracowników
- reklamą a obrotami
Populacja (zbiorowość statystyczna) - jest rozumiana jako zbiór wyników wszystkich elementów, które podlegają badaniu z punktu widzenia określonego kryterium.
Próba - jest podzbiorem populacji. Część populacji, która jest analizowana ze względu na ustaloną charakterystykę w celu wyciągnięcia wniosków dla całego zbioru (populacji).
Cecha statystyczna - własność jednostki; elementy wchodzące w skład populacji mają własności wspólne oraz takie, które różnicują te jednostki między sobą.
Zbiór danych może być rozpatrywany:
*z punktu widzenia:
- opisowego
- wnioskowania statystycznego
Podział cech statystycznych:
Jednym z wielu podziałów cech jest:
*Mierzalne
- wartości dają się wyrazić za pomocą liczb skokowe
- wyrażone w różnych jednostkach: zł, tonach, sztukach, itd... ciągłe
*Niemierzalne
- nie dają się zmierzyć nominalne, np. płeć, zawód, kolor..
- opisane na skali nominalnej porządkowe
Miary statystyczne:
- miary położenia
- miary rozproszenia
- miary asymetrii
- miary koncentracji
Miary położenia (tendencji centralnej):
- P-percentylem w zbiorze liczb (uporządkowanych według wielkości) mierzy skupienie się jednostek w znaczeniu procentowym; możemy określić procent zbiorowości znajdujący się poniżej danej obserwacji. Szczególne percentyle: mediana i kwartale,
- Dominanta(wartość modalna, moda )jest wartość, która w tym zbiorze występuje najczęściej
- Średnia arytmetyczna (średnia klasyczna)zwaną także przeciętną jest to suma wartości wszystkich wyników podzielona przez ich liczbę
Miary zróżnicowania:
- Rozstęp - - Wariancja - w zbiorze wyników wariancją nazywamy przeciętne kwadratowe odchylenie poszczególnych wyników od ich średniej
- Odchylenie standardowe
- Odchylenie przeciętne
jest średnią arytmetyczną bezwzględnych różnic pomiędzy poszczególnymi wartościami cechy a wartością średnią
Porównanie stopnia zróżnicowania dwóch zbiorowości: posługujemy się względnymi miernikami
![]()
![]()
są to współczynniki zmienności ich wartość wyznaczamy jako stosunek odchylenia standardowego lub przeciętnego do wartości średniej arytmetycznej pomnożony przez 100
Miary asymetrii (skośności)
Jeżeli dla tego samego zbioru danych obliczamy średnią arytmetyczną, medianę i dominantę to pomiędzy nimi może zachodzić jedna z trzech relacji (zależności):
- x = Me = D (występuje w szeregu symetrycznym)
- x < Me < D (skośność ujemna; lewostronna)
- D < Me < x (skośność prawostronna, dodatnia)
![]()
Miarą asymetrii jest współczynnik asymetrii WAS
Zmienne losowe i ich rozkłady
- jest to funkcja, która przy zajściu każdego zdarzenia losowego w przyjmuje konkretną wartość x(w), co zapisujemy:X: w რ x(w) Є R
Zmienna losowa może być:
*skokowa (dyskretna),
gdy może przyjmować wartości ze zbioru przeliczalnego. Rozkładem prawdopodobieństwa zmiennej losowej skokowej jest tablica, wzór lub wykres, który przyporządkowuje prawdopodobieństwa każdej możliwej wartości zmiennej.
Rozkład prawd. zmiennej losowej skokowej spełnia warunki:
- P(X=x)=P(x) Ⴓ 0 dla każdego x
- SP(xi) = 1
![]()
Dystrybuanta zmiennej losowej skokowej:
Własności dystrybuanty zmiennej skokowej:
- F(x) jest niemalejąca
- F(x) jest lewostronnie ciągła
- przy xრnieskończoności F(x) რ 1
*ciągła, gdy przyjmuje wartości z dowolnego przedziału liczbowego. Możliwe wartości takiej zmiennej tworzą zbiór nieprzeliczalny. Ciągła zmienna losowa to taka zmienna losowa, która może przyjmować dowolne wartości z pewnego przedziału nieprzeliczalnego
Prawdopodobieństwa związane z ciągłą zmienną losową X są wyznaczane przez funkcję gęstości prawdopodobieństwa zmiennej losowej.
Tą funkcję oznaczamy f(x) i ma ona następujące własności:
- f(x)Ⴓ0, dla każdego x
- prawdopodobieństwo, że X przyjmie wartość między a i b jest równe mierze pola pod krzywą f(x) pomiędzy punktami a i b
- całe pole pod krzywą f(x) jest równe 1
Rozkład dwumianowy zakłada przeprowadzenie eksperymentu polegającego na wykonaniu ciągu identycznych doświadczeń spełniających następujące warunki:
- Są dwa możliwe wyniki każdego doświadczenia, nazywane sukcesem i porażką. Wyniki te wykluczają się i dopełniają.
- Prawdopodobieństwo sukcesu oznaczane przez p , pozostaje takie samo od doświadczenia do doświadczenia. Prawd. porażki oznaczane przez q, jest równe 1-p.
- Doświadczenia są niezależne od siebie
Dwumianowy rozkład prawdopodobieństwa:
![]()
![]()
![]()
Rozkład Poissona
Rozkład ten jest dobrym przybliżeniem rozkładu dwumianowego, przy założeniu, że liczba doświadczeń n jest duża (n>20), a prawdopodobieństwo sukcesu jest małe (p<0,05)
Znajduje zastosowanie w ustalaniu prawdopodobieństwa wadliwości produkcji lub awaryjności maszyn
![]()
Rozkład normalny (Gaussa)
- Rozkład normalny jest rozkładem, do którego dąży m.in. rozkład dwumianowy gdy liczba doświadczeń n wzrasta
- Okazuje się, że rozkład normalny jest rozkładem granicznym wielu innych rozkładów, w sytuacjach gdy ujawniają się skutki różnych przypadkowych czynników pochodzących z różnych źródeł
Funkcja gęstości:
![]()
Standaryzowany rozkład normalny
- Ponieważ istnieje nieskończenie wiele normalnych zmiennych losowych, jedną z nich wybieramy aby służyła jako pewien standard. Prawdopodobieństwa związane z wartościami przyjmowanymi przez zmienną normalną standaryzowaną zostały stablicowane
- oznaczamy: N(0, 1)
Rozkład t-Studenta
Jeżeli mamy dwie zmienne losowe:
- U o rozkładzie normalnym standaryzowanym oraz
- c2 o średniej równej k oraz odchyleniu standardowym
to zmienna losowa:
![]()
Rozkład t-Studenta to rozkład charakterystyczny dla próbek o małej liczności (ozn. n).
Rozkład t charakteryzuje się stopniami swobody oznaczanymi jako k lub df.
Wartość przeciętna rozkładu t-Studenta jest równa zero, a jego wariancja przy df>2 jest równa df/(df-2). W miarę jak liczba df wzrasta, wariancja rozkładu t zbliża się do jedności, tj. do wariancji rozkładu Nၾ(0, 1).
ESTYMACJA
Z prób reprezentatywnych obliczamy wielkości statystyk, które są estymatorami określonych parametrów populacji.
Wyróżnia się dwa rodzaje estymacji:
- estymację punktową:
czyli metodę szacunku, za pomocą której jako wartość parametru zbiorowości generalnej przyjmuje się konkretną wartość estymatora wyznaczonego na podstawie n-elementowej próby (zakładamy, że wartość statystki z próby leży blisko wartości parametru populacji)
- estymację przedziałową:
za pomocą której wyznacza się przedział liczbowy, który z ustalonym prawdopodobieństwem zawiera nieznaną wartość szacowanego parametru zbiorowości generalnej.
Własności estymatorów:
- Estymator jest nieobciążony, jeżeli jego wartość oczekiwana jest równa parametrowi populacji, do oszacowania której służy
- Estymatora jest efektywny, jeżeli ma niewielką wariancję (a tym samym niewielkie odchylenie standardowe)
- Estymator jest zgodny, jeżeli prawdopodobieństwo, że jego wartość będzie bliska wartości szacownego parametru, wzrasta wraz ze wzrostem liczebności próby.
Przedziałem ufności nazywamy przedział liczbowy, o którym przypuszczamy, z określonym prawdopodobieństwem, że mieści się w nim nieznany parametr populacji
Centralne twierdzenie graniczne - Jeżeli pobieramy próbę z populacji o średniej μ i skończonym odchyleniu standardowym σ , to rozkład średniej z próby , dąży do rozkładu normalnego o średniej μ i odchyleniu, gdy liczebność próby wzrasta nieograniczenie, czyli dla „dostatecznie dużych n.
Rozkład chi-kwadrat
- Rozkład ten podobnie jak rozkład t, charakteryzuje się liczba stopni swobody, df ( df=n-1 )
- W przeciwieństwie do rozkładu t, rozkład chi-kwadrat nie jest symetryczny
- Rozkład chi-kwadrat jest rozkładem prawdopodobieństwa sumy kwadratów niezależnych, standaryzowanych, normalnych zmiennych losowych.
Stosuje się dwie grupy testów:
parametryczne i nieparametryczne
- stosowanie pierwszych wymaga przyjęcia założeń o postaci rozkładu testowanej zmiennej losowej oraz znajomości wybranych statystyk
- testy nieparametryczne takich założeń nie wymagają, ale nie są tak mocne jak parametryczne
Hipotezy statystyczne
Hipoteza statystyczna to każde przypuszczenie dotyczące rozkładu zmiennej losowej weryfikowane na podstawie n-krotnej realizacji tej zmiennej
Wyróżniamy:
- Hipotezy
parametryczne i nieparametryczne
proste i złożone
- Hipotezą zerową, oznaczoną przez H0, jest hipoteza w wartości jednego z parametrów populacji (lub wielu).
Tę hipotezę traktujemy jako prawdziwą, dopóki nie uzyskamy informacji statystycznych dostatecznych do zmiany naszego stanowiska
- Hipotezą alternatywną, oznaczoną przez H1, jest hipoteza przypisująca parametrowi (parametrom) populacji wartość inną niż podaje to hipoteza zerowa
Mocą testu hipotezy statystycznej jest prawdopodobieństwo odrzucenia hipotezy zerowej, gdy jest ona fałszywa. moc testu = 1-β
Własności mocy testu:
- Moc zależy od odległości między wartością parametru zakładaną w hipotezie zerowej a prawdziwą wartością parametru. Im większa odległość tym większa moc.
- Moc zależy od wielkości odchylenia standardowego w populacji. Im mniejsze odchylenie tym większa moc.
- Moc zależy od liczebności próby. Im liczniejsza próba, tym większa moc.
- Moc zależy od poziomu istotności testu. Im niższy poziom istotności tym mniejsza moc testu
Testy nieparametryczne
- test zgodności chi-kwadrat, populacja ma określony typ rozkładu
- test serii, sprawdzenie czy próba jest losowa?
- test rangowanych znaków, czy dwie próby pochodzą z tej samej populacji?
Regresja to
*modelowanie związku pomiędzy dwoma zmiennymi: zależną Y oraz niezależną X
- regresja liniowa: model liniowy
- regresja wieloraka: model nieliniowy
*Analiza efektów zmian wartości pojedynczych zmiennych objaśniających.
*Prognoza wartości zmiennej objaśnianej dla danego zestawu wartości zmiennych objaśniających.
*Badanie, czy jakakolwiek zmienna objaśniająca ma istotny wpływ na zmienną objaśnianą.
Korelacja wyraża stopień powiązania pomiędzy zmiennymi losowymi
- Korelacja pomiędzy dwoma zmiennymi losowymi X i Y
- w analizie korelacji badacz jednakowo traktuje obie zmienne: zależną i niezależną
- pokazuje ona, na ile obie zmienne zmieniają się równocześnie w sposób liniowy
- korelacja między X i Y jest taka sama jak między Y i X
- Korelacja między dwiema losowymi zmiennymi X i Y jest miarą siły (stopnia) liniowego związku między tymi zmiennymi
- Silnie skorelowane zmienne zachowują się tak, jak gdyby równocześnie się poruszały
- kowariancja parametr charakteryzujący zależności pomiędzy zmiennymi X i Y
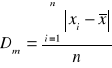
![]()
![]()
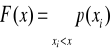
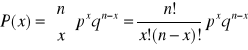
![]()
![]()
![]()
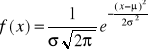
Wyszukiwarka
Podobne podstrony:
stataystyka, Politechnika Poznańska, Magisterka ZIiP, Semestr I (VIII), Statystyka
ekologia-pytania, Politechnika Poznańska, Magisterka ZIiP, Semestr I (VIII), Ekologia w przemyśle
ESPćw1sc, Politechnika Poznańska, Magisterka ZIiP, Semestr I (VIII), Elastyczne systemy produkcyjne
ekoinżynieria-teoria, Politechnika Poznańska, Magisterka ZIiP, Semestr I (VIII), Ekoinzynieria środo
KSSP - CAx, Politechnika Poznańska, Magisterka ZIiP, Semestr I (VIII), Komputerowe systemy sterowani
ekologia-na-długopis, Politechnika Poznańska, Magisterka ZIiP, Semestr I (VIII), Ekologia w przemyśl
Tworzywa polimerowe ściąga druk, Politechnika Poznańska, Studia- materiały, Semestr 2, Przetwórstwo
egzamin sciaga tk, Politechnika Poznańska - Zarządzanie i Inżynieria Produkcji, Semestr III, Technol
sciaga odlewanie, Politechnika Poznańska (ETI), Semestr I i II, Metalurgia I Odlewnictwo
materialoznastwo-sciaga, studia, studia Politechnika Poznańska - BMiZ - Mechatronika, 1 semestr, mat
sciaga-moja, studia, studia Politechnika Poznańska - BMiZ - Mechatronika, 2 semestr
sciaga-moja, studia, studia Politechnika Poznańska - BMiZ - Mechatronika, 2 semestr
sciaga materialy, Politechnika Poznańska ZiIP, I semsetr, NOM, NoM II, NoM
Wozniak-oprzyrzadowanie - ściąga, MiBM Politechnika Poznanska, VI semestr TPM, Miut, archiwa, MiUT I
Za wynalazki SCIAGA, MiBM Politechnika Poznanska, VII semestr TPM, Ochrona Własności Intelektualnej,
więcej podobnych podstron