1. Zasady pomiaru.

Emisja elektronów z powierzchni metali ogrzanych do odpowiedniej temperatury nosi nazwę termoemisji. Decydujące znaczenie ma w tym zjawisku wartość liczbowa tzw. pracy wyjścia elektronu z metali. Określamy ją jako minimum energii, którą musi posiadać elektron w celu pokonania bariery potencjału wywołanej napięciem kontaktowym. Im mniejsza wartość pracy wyjścia z danego materiału, w tym niższej temperaturze będzie zachodzić termoemisja. W niniejszym ćwiczeniu wyznaczamy pracę wyjścia elektronu, wykorzystując zjawiska występujące w lampie elektronowej.

Żarzona katoda emituje elektrony, które w skutek przyłożonego napięcia między katodą i anodą (o odpowiedniej polaryzacji) są przez tę ostatnią wychwytywane. Przez lampę płynie więc prąd, którego gęstość nasycenia możemy obliczyć ze wzoru Richardsona - Dushmana. Logarytmując wzór Richardsona - Dushmana i dokonując pewnych uproszczeń oraz wykreślając uzyskaną zależność otrzymujemy prostą tzw. prostą Richardsona. Wyznaczenie pracy wyjścia elektronu w naszym ćwiczeniu będzie więc polegało na otrzymaniu prostej Richardsona z uzyskanych wartości pomiarowych j_n przy danej temperaturze katody, a następnie obliczenia tangensa nachylenia tej prostej.

2. Układ pomiarowy.

3. Ocena dokładności pojedynczych pomiarów.

Podczas wykonywania ćwiczenia korzystaliśmy z voltomierza klasy 0.5, który pracował w zakresie 7.5V. Do pomiaru prądu I_n używaliśmy amperomierza klasy 0.5. Pracował on w zakresie 7.5mA jednak przed wykonaniem 4 ostatnich pomiarów musieliśmy zmienić zakres na 30mA. Prąd żażenia ustawialiśmy za pomocą przeznaczonych do tego celu potencjometrów znajdujących się na płycie czołowej zasilacza.

4. Tabele pomiarowe.

Tabela 1.

Ua=150V
Iż±ΔIż	Uż±ΔUż	In±ΔIn
A	V	mA
0.54±0.04	1,3±0,02	0,4±0,04
0.56±0.04	1.45±0,02	1±0,04
0.58±0.04	1,55±0,02	1,5±0,04
0.6±0.04	1,7±0,03	3,2±0,04
0.62±0.04	1,8±0,03	5,2±0,04
0.64±0.15	1,9±0,03	8,5±0,08
0.66±0.15	2,0±0,03	13±0,08
0.68±0.15	2,15±0,03	21,5±0,15
0.7±0.15	2,2±0,03	28,5±015

Do dalszych obliczeń potrzebne będą także wielkości, które przepisaliśmy z instrukcji:

S_k=1cm²

ε=0.5

δ=5.76⋅10^-12

Tabela 2.

Pż±ΔPż	T	1/T±Δ1/T	Jn	lnJn
W	K	K^-1	mA/cm^2
0,7±0,062	704,9	0,00143±3,2*10^-5	0,4	-0,92
0,8±0,067	728,8	0,00138±2,9*10^-5	1	0
0,9±0,076	750,6	0,00136±2,9*10^-5	1,5	0,41
1,0±0,088	770,7	0,00124±2,7*10^-5	3,2	1,16
1,1±0,096	789,2	0,00125±2,7*10^-5	5,2	1,65
1,2±0,29	806,6	0,00125±7,5*10^-5	8,5	2,14
1,3±0,32	822,9	0,00124±7,6*10^-5	13	2,56
1,5±0,35	852,9	0,00117±6,8*10^-5	21,5	3,07
1,7±0,38	879,9	0,00113±6,3*10^-5	28,5	3,35

5. Przykładowe obliczenia wielkości złożonej.

Moc właściwa katody, czyli moc żarzenia przypadającą na jednostkę powierzchni katody obliczamy ze wzoru :

Uż * Iż

Pż = ----------

Sk

gdzie :

Pż - moc właściwa katody

Iż - prąd żarzenia

Sk - powierzchnia katody, dla lampy elektronowej AZ-1 przyjeliśmy, że Sk = 1 cm²

np. dla pomiaru nr 1 :

1,3 V * 0,54 A

Pż = ---------------------- = 0,702 W

1 cm²

Temperaturę katody wyznacyliśmy ze wzoru :

______

| Pż

T = 4| --------

\| ε*σ

gdzie :

Pż - moc właściwa katody

W

σ - stała = 5,76 * 10^-12 ----------

cm²*K⁴

ε - emisyjność całkowita równa 0,5 dla katody lampy AZ-1

np. dla pomiaru nr 1 : ________________

| 0,702

T = 4| ---------------------- = 704,9K

\| 0,5 * 5,76 * 10^-12

Przykładowe obliczenie wartości 1/T dla pomiaru nr 1 :

1 / 704,9 = 0,00143 K^-1

Gęstość prądu nasycenia obliczyliśmy ze wzoru :

In

j_n = -----

Sk

gdzie :

j_n - gęstość prądu nasycenia ,

In - natężenie prądu nasycenia ,

Sk - powierzchnia katody, dla lamy elektronowej AZ-1 przyjeliśmy Sk = 1 cm²

np. dla pomiaru nr. 1:

0,4 mA

j_n = ------------ = 0,4mA/cm²

1 cm²

Przykładowe obliczenie wartości lnj_n dla pomiaru nr 1 :

ln 0,4= -0,92

Praca wyjścia elektronu z katody

W = kB ⋅ tgα

Z tabeli odczytuję wartości ln(j_n) i (1/T) potrzebne do określenia kąta nachylenia prostej na wykresie ln(j_n) = f ( 1/T ):

gdzie n jest kolejną liczbą pomiarów

i tak:

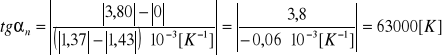
W = k⋅tgα

wiedząc, że k = 1,38⋅10^-23 [J⋅K^-1]

W = 1,38⋅10^-23 [J⋅K^-1]⋅ 63000 [K] ≈ 869⋅10^-21 [J]

Odczytując z tablic 1[eV] = 1,602177⋅10^-19 [J] Można podać wartość pracy wyjścia W w [eV]

4.Racunek błędów

Sposób obliczania błędów pomiarów, takich jak : Uż, In przestawiliśmy w punkcie III (Ocena dokładności pojedyńczych pomiarów).

Błąd ΔPż (moc właścia katody) obliczyliśmy ze wzoru :

( |ΔUż| |ΔIż| )

ΔPż = (|-----| + |-----|) * Pż

(| Uż | | Iż |)

np. dla pomiaru nr 1 :

(|0,04 A| |0,02 V|)

ΔPż = (|----------| + |----------|) * 0,702 W = 0,062 W

(| 0,54 A| | 1,3 V |)

Błąd Δ1/T obliczyliśmy ze wzoru :

Δ1/T = 1/4*(ΔPż / Pż)* 1/T

np. dla pomiaru nr 1 :

Δ1/T = 1/4*(0,062W / 0,702 W) * 0,00143 K^-1 = 0,0000032 K^-1

8. Wnioski

Po wykreśleniu prostej Richardsona i określeniu jej kąta nachylenia względem osi 1/T można było określić pracę wyjścia elektronu z katody lampy AZ-1. W tym przypadku praca ta wynosi 1,54 eV . Na podstawie tego można stwierdzić że materiałem użytym do wykonania katody był prawdopodobnie wolfram. Wszystkie pomiary obarczone są pewnym błędem wynikającym z niedokładności odczytu wielkości mierzonych. Na błędy może mieć także wpływ konieczność oczekiwania na ustalenie się temperatury katody. Nie za każdym razem czas oczekiwania był wystarczająco długi. Przy wyznaczaniu pracy wyjścia mógł pojawić się błąd wynikający z określenia nachylenia prostej ln jn = f(1/T).

---