Instrukcja laboratoryjna nr 1

WYZNACZENIE OPORU I LICZBY OPORU RUROCIĄGU (WYROBISKA) ORAZ LICZBY OPORU MIEJSCOWEGO

1. Wprowadzenie

Dyssypacja energii i opór bocznicy sieci wentylacyjnej

Dla wyznaczenia oporu rurociągu wychodzi się np. z potencjału izentropowego. Zgodnie z definicją jest on równy

(1)

gdzie:

- całkowity potencjał izentropowy, J/m³ ,

- ciśnienie całkowite w punkcie dla którego wyznaczamy potencjał, Pa,

- ciśnienie powietrza suchego (nieruchomego) ulegającego przemianie izentropowej w punkcie dla którego wyznaczamy potencjał, Pa, przy czym

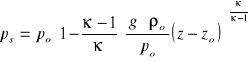
(2)

- ciśnienie statyczne, bezwzględne powietrza na zrębie szybu wdechowego, uważanym za główny wlot do sieci, Pa,

- wykładnik izentropy;
= 1,4,
g - przyspieszenie siły ciężkości; g = 9.80665 m/s² ,

ρ - gęstość powietrza na zrębie szybu wdechowego, kg/m³ ,

- wysokość niwelacyjna zrębu szybu wdechowego, m,
z - wysokość niwelacyjna punktu dla którego wyznaczamy potencjał, m.

Spadek całkowitego potencjału izentropowego
w bocznicy sieci wentylacyjnej wyznacza się z zależności;

(3)

gdzie:

- całkowity potencjał izentropowy w węźle dopływowym bocznicy (wyrobiska), J/m³ ,

- całkowity potencjał izentropowy w węźle wypływowym bocznicy (wyrobiska), J/m³.

Z teorii tego potencjału wiadomo [1], że jego spadek w ogólnym przypadku jest równy

(4)

gdzie:

- dyssypacja energii w bocznicy (wyrobisku), J/m³,

- dyssypacja energii w oporze lokalnym (miejscowym), J/m³,

- depresja naturalna generowana w bocznicy (wyrobisku), J/m³,

- spiętrzenie całkowitej energii wentylatora (praca techniczna doprowadzona do wentylatora), J/m³.

Dla prostoosiowego, poziomego odcinka (I - II) rurociągu bez wentylatora (rys.1)
= 0;
= 0 i
= 0. Wobec tego wzór (4) przyjmie postać

(5)

Dyssypację energii w bocznicy (wyrobisku) (pracę tarcia przypadającą na 1m³ przepływającego powietrza) wyznacza się z zależności

(6)

gdzie:

- gęstość powietrza wyznaczona dla warunków normalnych, t j. p = 760 Tr i t = 20°C,
= l. 20 kg/m³,

- gęstość średnia powietrza w bocznicy (wyrobisku) , kg/m³, równa

(7)

- odpowiednio gęstość powietrza w przekroju dopływu (d) i przekroju wypływu (w), kg/m3,

- strumień objętości powietrza sprowadzony do warunków normalnych, m³/s, przy czym

(8)

- strumień objętości powietrza, m³/s, wyznaczany ze wzoru

(9)

w - prędkość średnia powietrza w wyrobisku, m/s,

A - pole przekroju poprzecznego wyrobiska, m ,

- opór właściwy wyrobiska, kg/m⁷, przy czym

(10)

- liczba oporu wyrobiska,

B - obwód wyrobiska, m,

L - długość wyrobiska, m.

Chcąc wyznaczyć np. opór wyrobiska istniejącego, zgodnie z zależnościami (5÷10), należy, w oparciu o pomiary, wyznaczyć między innymi spadek całkowitego potencjału izentropowego powietrza.

Korzystając ze wzorów (3) i (1) można napisać

(11)

Dla wyrobiska (rurociągu) poziomego
, a tym samym zgodnie z zależnością (2)
. W związku z tym wzór (11) przyjmie postać

(12)

Zgodnie z tą zależnością, spadek całkowitego potencjału izentropowego w tym przypadku jest równy różnicy ciśnień całkowitych pomierzonych w przekrojach dopływowym (d) i wypływowym (w) wyrobiska (rurociągu). Różnicę tą, można pomierzyć za pomocą, rurek Prandtla, grubościennego węża gumowego i przyrządu mierzącego różnicę ciśnień np. mikromanometru z rurką pochyłą (rys.1).

Jeśli zamiast rurek Prandtla zastosujemy tarczki Sera to zgodnie z zależnością

(13)

dla wyznaczenia różnicy ciśnień całkowitych jest konieczny pomiar różnicy ciśnień statycznych (stosując tarczki Sera, grubościenny wąż gumowy i mikromanometr) oraz wyznaczenie różnicy ciśnień kinetycznych w oparciu o prędkości średnie i gęstości powietrza wyznaczone dla przekrojów dopływowego (d) i wypływowego (w) wyrobiska (rurociągu).

Dyssypacja energii w oporze miejscowym (lokalnym). Opór miejscowy

- dla bocznicy istniejącej

Wychodzimy z równania ruchu w postaci:

(14)

Przyjmujemy, że:

i

otrzymujemy:

(15)

Zakładając ponadto, że
i całkując wzdłuż drogi od
do
uzyskujemy:

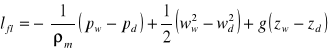
(16)

gdzie

[
] = J/kg.

Jeśli dyssypację energii odniesiemy do 1 m³ powietrza

(17)

[
] = J/m³.

Przyjmując, że

oraz

otrzymamy:

(88)

lub

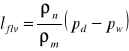
(19)

Wzory (16÷19) pozwalają wyznaczyć dyssypację energii na oporze miejscowym (lokalnym) w bocznicy istniejącej, dla której możemy dokonać pomiarów stosownych parametrów.

• dla bocznicy projektowanej

Dyssypację energii w oporze miejscowym wyznacza się ze wzoru:

(20)

przy czym

[
]= m²/s²*kg/kg = J/kg.

Wiedząc, że

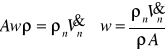
równanie (20) przyjmie postać:

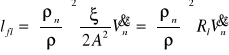
(21)

gdzie:

- dyssypacja energii w oporze miejscowym, J/kg,

- opór miejscowy (lokalny) aerodynamiczny, m^-4, przy czym

(22)

- liczba oporu miejscowego (lokalnego).

Równanie (21) w odniesieniu do 1 m³ powietrza przyjmie postać:

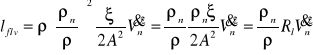
(23)

(24)

gdzie:

- opór miejscowy właściwy, kg/m⁷.

Liczby oporu miejscowego dla najczęściej występujących w kopalniach oporów miejscowych podawane są w literaturze.

2. Zakres materiału do opanowania

1. Teoria potencjału izentropowego,

2. Wyznaczanie gęstości powietrza kopalnianego,

3. Metody pomiaru prędkości średniej powietrza w wyrobisku (rurociągu),

4. Pomiary parametrów interweniujących w zależnościach (1) ÷ (13), takich jak:

• ciśnienie statyczne, bezwzględne powietrza p,

• różnica ciśnień całkowitych
  ,

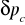
• różnica ciśnień statycznych
  ,

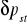
• różnica ciśnień kinetycznych
  ,

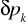
• pole przekroju poprzecznego wyrobiska (rurociągu) A,

• obwód wyrobiska (rurociągu) B,

• temperatura na termometrze suchym
  ,

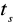
• temperatura na termometrze mokrym
  ,

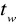
5. Stosowane przyrządy i metody pomiarowe parametrów wymienionych w
punkcie 4,

6. Znajomość podstawowych pojęć z tego zakresu, takich jak:

• potencjał powietrza,

• spadek potencjału powietrza,

• dyssypacja energii w wyrobisku (rurociągu) i oporze miejscowym,

• depresja naturalna generowana w wyrobisku nachylonym,

• opór właściwy, normalny i aerodynamiczny wyrobiska,

• współczynnik oporu, liczba oporu,

• liczba oporu miejscowego.

3. Przebieg ćwiczenia

Na stanowisku (rys.1) zmierzyć:

• różnicę ciśnień całkowitych
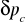
  między przekrojami dopływu (d) i wypływu (w) rurociągu,

• średnicę rurociągu D,

• długość rurociągu L między przekrojami (d) i (w),

• prędkość średnią powietrza w rurociągu,

• temperaturę powietrza na termometrze suchym i mokrym (psychro­­m­etrem ­­­Asmanna),

• ciśnienie statyczne, bezwzględne powietrza (barometrem lub baroluksem).

Rys. 1. Stanowisko do wyznaczania oporu rurociągu

Na stanowisku (rys.2) zmierzyć:

• różnicę ciśnień
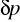
  między przekrojami dopływu (d) i wypływu (w) oporu miejscowego,

• średnicę rurociągu D,

• ciśnienie dynamiczne w środku rurociągu w celu wyznaczenia met. punktową prędkości średniej powietrza w rurociągu,

• temperaturę powietrza na termometrze suchym i mokrym (psychro­­m­etrem ­­­Asmanna),

• ciśnienie statyczne, bezwzględne powietrza (barometrem lub baroluksem).

Rys. 2. Stanowisko do wyznaczania oporu miejscowego

4. Obliczenia

W oparciu o wyniki pomiarów obliczyć:

• gęstość powietrza w rurociągu,

• dyssypację energii w rurociągu,

• opór właściwy, normalny i aerodynamiczny rurociągu,

• współczynnik oporu rurociągu,

• liczbę oporu,

• dyssypację energii w oporze miejscowym,

• opór miejscowy (właściwy),

• liczbę oporu miejscowego.

5. Sprawozdanie

Powinno zawierać:

1. Wstęp teoretyczny

2. Dane techniczne stanowiska pomiarowego i jego schemat ideowy

3. Dane techniczne stosowanych przyrządów

4. Wyniki pomiarów

5. Tok obliczeń obejmujący wyznaczenie:

• gęstości powietrza,

• strumień objętości powietrza
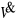
  i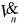
  

• dyssypację energii w rurociągu,

• opór właściwy, normalny i aerodynamiczny rurociągu,

• współczynnik oporu rurociągu,

• liczbę oporu rurociągu,

• dyssypację energii w oporze miejscowym,

• opór miejscowy właściwy,

• liczbę oporu miejscowego.

6. Wnioski i dyskusję błędów

7. Protokół z pomiarów (wyniki pomiarów powinny być prowadzone na oddzielnej kartce). Protokół powinien zawierać:

• listę osób realizujących ćwiczenie,

• wyniki pomiarów zatwierdzone przez prowadzącego.

Rys. 2. Nomogram do wyznaczania prędkości średniej w_m na podstawie

punktowego pomiaru prędkości maksymalnej w osi przewodu kołowego

6. LITERATURA

[1] Nędza Z., Rosiek F.: Wentylacja kopalń cz. I i II, Skrypt Politechniki Wrocławskiej, Wrocław 1981

[2] Bystroń H.: Stacjonarne pola potencjalne w kopalnianej sieci wentylacyjnej. Przegląd Górniczy 1974 nr 10

[3] Roszczynialski W., Trutwin W., Wacławik J.: Kopalniane pomiary wentylacyjne, Wyd. „Śląsk”, Katowice 1992

[4] Rosiek F.: Materiały pomocnicze do ćwiczeń.

---