Egzamin, SGH studia dzienne, grudzień 2006. TEMAT A.
Przy rozwiązaniach zadań jeśli jest to konieczne należy przyjąć poziom istotności 0,05 i współczynnik ufności 0,95.
Dwóch nauczycieli porównało wyniki sprawdzianu pisemnego z matematyki wśród uczniów prowadzonych przez nich klas szkoły podstawowej prywatnej i państwowej. Do porównania wykorzystali następujące wartości charakterystyk opisujących wyniki klas:
Na podstawie otrzymanych informacji oceń prawdziwość poniższych wniosków wyciągniętych przez nauczycieli. Uzasadnij odpowiedź wyznaczając odpowiednie miary wraz z interpretacją.
1. Uczniowie badanej klasy ze szkoły prywatnej charakteryzują się wyższym poziomem przeciętnych wyników sprawdzianu z matematyki niż uczniowie z klasy ze szkoły państwowej.
2. Zróżnicowanie wyników uczniów w szkole państwowej było większe niż uczniów w szkole prywatnej.
3. Rozkład wyników uczniów z klasy ze szkoły państwowej charakteryzuje się asymetrią ujemną.
4. Którą szkołę można rekomendować osobie wysyłającej dziecko do szkoły i dlaczego?
Kierownictwo sklepu osiedlowego „Alina” zamierza dokonać reorganizacji pracy w sklepie. Wcześniej postanowiło przeprowadzić potrzebne badania statystyczne.
Aktualnie na dziale” słodycze” sprzedawane są czekolady orzechowe, mleczne, gorzkie i białe. Kierownictwo sklepu zastanawia się nad popularnością poszczególnych typów czekolad. Jaką liczebność powinna mieć losowa próba klientów sklepu, aby maksymalny błąd szacunku odsetka klientów kupujących czekolady mleczne nie przekroczył 5 pkt. proc.? Pilotażowo pytanie o czekolady mleczne zadano 90 klientom, z których 30 potwierdziło, że je kupuje.
Spośród 120 innych losowo wybranych klientów 96 uznało, że kupuje czekolady z orzechami. Z kolei 60 z 90 jeszcze innych losowo wybranych klientów przyznało, że kupuje czekolady gorzkie. Czy można się zgodzić z twierdzeniem, że więcej klientów „Aliny” kupuje czekolady z orzechami niż czekolady gorzkie? Zweryfikuj stosowną hipotezę.
Pewnych zmian wymagają także inne działy:
Obserwacje prowadzone przez kasjerów wskazują, że 15% klientów odwiedzających sklep kupuje lokalny dziennik „Goniec”. Ile egzemplarzy gazety dziennie powinien zamawiać sklep, aby prawdopodobieństwo, że jej zabraknie nie przekroczyło 5%, jeśli oczekiwana liczba klientów odwiedzających sklep w ciągu jednego dnia wynosi 360? Dla uproszczenia należy założyć, że każdy klient kupuje tylko jeden egzemplarz „Gońca”.
Pracownicy działu warzywnego domagają się zmiany dostawcy pomarańczy twierdząc, że dostarczane przez niego pomarańcze psują się przed deklarowanym przez dostawcę terminem świeżości. Kierownictwo jest skłonne przychylić się do wniosku pracowników, jednak wcześniej chciałoby zdobyć jakieś dowody potwierdzające, że rzeczywiście pomarańcze psują się przed terminem. Zaproponuj metodę zweryfikowana odpowiedniej hipotezy. Jakie założenia należy przyjąć?
Weryfikując hipotezę dotyczącą świeżości pomarańczy otrzymano krytyczny poziom istotności (p-value) równy 0.03. Czy należy zmienić dostawcę pomarańczy? Odpowiedź uzasadnić.
Wybrano w sposób losowy 6 osób pracujących w Polsce w górnictwie i zapytano o staż pracy i liczbę zachorowań na choroby układu oddechowego w ciągu ostatniego roku otrzymując następujące informacje:
Na podstawie odpowiednich miar i analiz należy ustosunkować się do następujących stwierdzeń:
1. Korelacja liczby zachorowań względem stażu pracy wśród badanych pracowników charakteryzuje się dużą siłą i dodatnim kierunkiem.
2. Korelację liczby zachorowań względem stażu pracy w populacji osób pracujących w górnictwie w Polsce można uznać za istotną na poziomie istotności 0,01.
3. Decyzja podjęta w punkcie poprzednim ulegnie zmianie dla poziomu istotności 0,001.
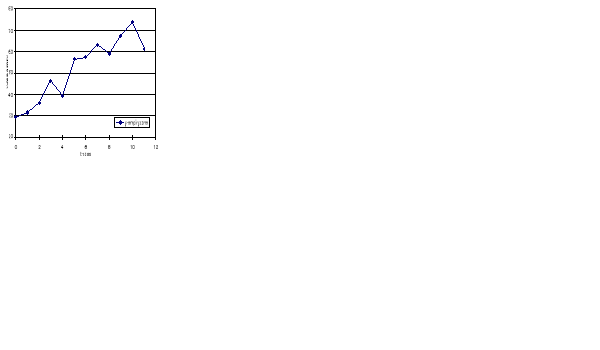
Poniższa tablica zawiera informacje dotyczące ceny ropy BRENT w Londynie w USD za baryłkę w latach 2004-2006 (informacja kwartalna, szereg empiryczny), dane szeregu wygładzone metodą analityczną (z wykorzystaniem funkcji liniowej), oszacowaną funkcję trendu kwartalnego oraz wskaźniki okresowości addytywnej dla trzech kwartałów.
|
|
|
|
Szereg wygładzony metodą analityczną
|
Szereg wygładzony metodą mechaniczną
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
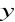
(t) = 3,80 t + 30, 89
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Oczyszczone wskaźniki okresowości addytywnej
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Korzystając z podanych informacji należy udzielić odpowiedzi (liczbowo + interpretacje) na następujące pytania i plecenia:
Ile razy wzrosła (lub zmalała) cena ropy w IV kwartale 2006 w porównaniu z I kwartałem 2005?
Czy średnie tempo zmian cen ropy za okres I.kw 2004 - I.kw 2005 było większe (mniejsze) od średniego tempa zmian za okres I.kw 2005 - I.kw 2006 ?.
Wygładź szereg empiryczny (dla okresu I-IV kwartał 2005) metodą mechaniczną (za pomocą średnich ruchomych). Przedstaw na zamieszczonym wykresie wyniki wyrównania szeregu dla tego okresu metodą analityczną i mechaniczną. Oceń, która metoda daje lepsze wygładzenie.
Jaką interpretację posiadają oszacowania parametrów strukturalnych kwartalnej funkcji trendu?
Oceń liczbowo i słownie okresowość w III kwartale?
Jakiej (teoretycznie) ceny ropy za baryłkę należy oczekiwać w III kwartale 2007 roku?
Zadanie 5. (otoczyć kółkiem prawidłową odpowiedź T-tak lub N-nie)
1. Określono typowy obszar zmienności 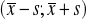
dla empirycznego rozkładu cechy. Czy można znaleźć w tym rozkładzie inny obszar wartości cechy o takiej samej rozpiętości i obejmujący co najmniej taką samą liczbę jednostek, jeśli rozkład jest:
jednomodalny symetryczny? T N
Na podstawie próby 30-elementowej nie odrzuciliśmy na poziomie istotności 0,05 hipotezy o tym, że średni wzrost osób w pewnej populacji wynosi 166cm. Czy to oznacza, że nie odrzucilibyśmy tej hipotezy również, gdyby
przyjąć poziom istotności 0,01 (przy innych warunkach nie zmienionych)? T N
pobrać z tej populacji inną 30-elementową próbę losową? T N
te same wyniki pochodziły z większej próby? T N
Czy analiza wariancji może być użyta do
a) sprawdzenia, że średnie w kilku populacjach są jednakowe? T N
b) sprawdzenia, że średnie w dwóch populacjach są jednakowe? T N
c) sprawdzenia, że wariancje w kilku populacjach są jednakowe? T N
Funkcja regresji liczby turystów (w tys.) odwiedzających pewne europejskie miasto w
lipcu względem średniej temperatury lipca (w stopniach Celsjusza) ma postać: 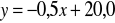
. Oznacza to, że
przy wzroście średniej temperatury o jeden stopień liczba turystów maleje
przeciętnie o 0,5 osoby T N
średnia liczba zwiedzających przy średniej temperaturze lipca 5 stopni
Celsjusza wyniesie 25 tysięcy osób (±błąd standardowy oceny), T N
zależność X i Y jest słaba. T N
Egzamin, SGH studia dzienne, grudzień 2006. TEMAT B.
Porównując czas jaki spędzają tygodniowo w świetlicy uczniowie 2 klasy szkoły podstawowej prywatnej i państwowej otrzymano następujące charakterystyki opisowe:
|
|
Średni czas spędzany na świetlicy w godz.
|
|
|
|
|
|
|
|
|
|
|
|
|
Na podstawie otrzymanych informacji oceń prawdziwość poniższych stwierdzeń. Uzasadnij odpowiedź wyznaczając odpowiednie miary wraz z interpretacją.
1. Uczniowie badanej klasy w szkole prywatnej spędzają przeciętnie więcej czasu w świetlicy niż uczniowie badanej klasy w szkole państwowej.
2. W szkole prywatnej zróżnicowanie czasu było większe (zinterpretuj zastosowaną miarę).
3. Kierunek asymetrii czasu spędzanego w świetlicy w obu szkołach jest taki sam.
4. Czy uzyskane wyniki liczbowe miar pozwalają na jednoznaczną rekomendację jednej ze szkół dla osoby wysyłającej dziecko do szkoły?
Właściciel stołówki planuje jej reorganizację. W zestawach obiadowych serwowanych przez stołówkę można zamówić cztery rodzaje naleśników: z jabłkami, z truskawkami, z czekoladą oraz z serem.
Właściciel zastanawia się nad popularnością poszczególnych rodzajów naleśników. Jaką liczebność powinna mieć losowa próba klientów stołówki, aby precyzja szacunku odsetka klientów lubiących naleśniki z czekoladą była nie mniejsza niż 4 pkt. proc.? Pilotażowo pytanie o naleśniki czekoladowe zadano 75 klientom, z których 15 stwierdziło, że je lubi.
Spośród 90 innych losowo wybranych klientów 60 uznało, że lubi naleśniki z jabłkami. Z kolei 75 ze 120 jeszcze innych losowo wybranych klientów przyznało, że lubi naleśniki z truskawkami. Czy można się zgodzić z twierdzeniem, że klienci stołówki lubią bardziej naleśniki z jabłkami niż z truskawkami? Zweryfikuj stosowną hipotezę.
Obserwacje prowadzone przez kasjerów wskazują, że 20% klientów odwiedzających sklep kupuje na deser specjalność zakładu - mrożoną galaretkę ze świeżym kiwi, która jest przygotowywana codziennie rano i nie nadaje się do sprzedaży następnego dnia. Ile porcji galaretki powinno być przygotowywane rano, aby prawdopodobieństwo, że jej zabraknie nie przekroczyło 5%, jeśli oczekiwana liczba klientów odwiedzających stołówkę jednego dnia wynosi 240? Należy założyć, że każdy klient kupuje tylko jedną porcję galaretki.
Pracownicy przygotowujący sałatki greckie domagają się zmiany dostawcy oliwek twierdząc, że owoce dostarczane przez niego psują się przed deklarowanym przez dostawcę terminem świeżości. Kierownictwo jest skłonne przychylić się do wniosku pracowników, jednak wcześniej chciałoby zdobyć jakieś dowody potwierdzające, że rzeczywiście oliwki psują się przed terminem. Zaproponuj metodę zweryfikowania odpowiedniej hipotezy. Jakie założenia należy przyjąć?
Weryfikując hipotezę dotyczącą świeżości oliwek otrzymano krytyczny poziom istotności (p-value) równy 0.13. Czy należy zmienić dostawcę oliwek? Odpowiedź uzasadnić.
Wybrano w sposób losowy 6 osób pracujących w Polsce w leśnictwie i zapytano o staż pracy i liczbę zachorowań na choroby układu ruchowego w ciągu ostatniego roku otrzymując następujące informacje:
Na podstawie odpowiednich miar i analiz należy ustosunkować się do następujących stwierdzeń:
1. Korelacja liczby zachorowań względem stażu pracy wśród badanych pracowników charakteryzuje się dużą siłą i dodatnim kierunkiem.
2. Korelację liczby zachorowań względem stażu pracy w populacji osób pracujących w leśnictwie w Polsce można uznać za istotną zakładając prawdopodobieństwo błędu I rodzaju na poziomie 1%.
3. Jeżeli zmniejszymy zakładane prawdopodobieństwo błędu I rodzaju do poziomu 1‰ to decyzja podjęta w poprzednim punkcie ulegnie zmianie.
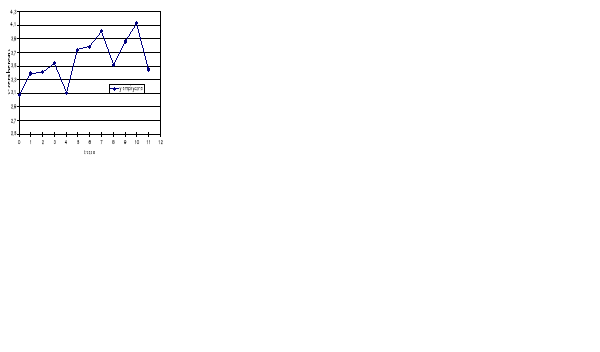
Poniższa tablica zawiera informacje dotyczące ceny litra benzyny (w PLN) w hurcie w Polsce w latach 2004-2006 (informacja kwartalna, szereg empiryczny), dane szeregu wygładzone metodą analityczną (z wykorzystaniem funkcji liniowej), oszacowaną funkcję trendu kwartalnego oraz wskaźniki okresowości addytywnej dla trzech kwartałów.
|
|
|
|
Szereg wygładzony metodą analityczną
|
Szereg wygładzony metodą mechaniczną
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
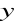
(t) = 0,057 t + 3,267
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Oczyszczone wskaźniki okresowości addytywnej
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Korzystając z podanych informacji należy udzielić odpowiedzi (liczbowo + interpretacje) na następujące pytania i plecenia:
Ile razy wzrosła (lub zmalała) cena 1 litra benzyny w IV kwartale 2006 w porównaniu z I kwartałem 2005?
Czy średnie tempo zmian ceny benzyny za okres I.kw 2004 - I.kw 2005 było większe (mniejsze) od średniego tempa zmian za okres I.kw 2005 - I.kw 2006 ?.
Wygładź szereg empiryczny (dla okresu I-IV kwartał 2005) metodą mechaniczną (za pomocą średnich ruchomych). Przedstaw na zamieszczonym wykresie wyniki wyrównania szeregu dla tego okresu metodą analityczną i mechaniczną. Oceń, która metoda daje lepsze wygładzenie.
Jaką interpretację posiadają oszacowania parametrów strukturalnych kwartalnej funkcji trendu?
Oceń liczbowo i słownie okresowość w III kwartale.
Jakiej (teoretycznie) ceny benzyny należy oczekiwać w III kwartale 2007 roku ?
Zadanie 5. (otoczyć kółkiem prawidłową odpowiedź T-tak lub N-nie)
1. Zmienna losowa X ma rozkład N(m,σ). Czy prawdziwe są zdania:
pole pod krzywą gęstości rozkładu X jest jednakowe niezależnie od
wartości parametru σ? T N
b) wartość zmiennej X równa m+1,96σ jest kwantylem rozkładu rzędu 0,95? T N
c) wartości m-σ i m+σ różnią się tylko znakami? T N
Hipotezy o tym, że średnia waga osób w pewnej populacji wynosi 80 kg, względem alternatywy, że jest ona różna od 80kg, nie odrzuciliśmy na poziomie istotności 0,05. Czy to oznacza, że nie odrzucilibyśmy tej hipotezy również wtedy, gdyby
hipoteza alternatywna była lewostronna T N
pobrać inną próbę losową o tej samej liczebności, T N
przyjąć poziom istotności 0,1 (przy innych warunkach nie zmienionych). T N
Czy analiza wariancji może być użyta:
a) gdy wariancje w porównywanych populacjach są różne? T N
b) gdy średnie w porównywanych populacjach są różne? T N
c) do sprawdzenia, że średnie w dwóch populacjach są jednakowe? T N
Funkcja regresji liczby turystów odwiedzających pewne europejskie miasto w
lipcu względem średniej temperatury lipca (w stopniach Celsjusza) ma postać: 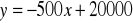
. Oznacza to, że
zależność X i Y jest silna, T N
w każdym przypadku wzrost średniej temperatury o jeden stopień powoduje
spadek liczby turystów o 500 osób T N
średnia liczba zwiedzających przy średniej temperaturze lipca 0 stopni
Celsjusza wyniesie 20 tysięcy osób (± błąd standardowy oceny). T N
![]()