Politechnika Œl¹ska

Wydzia³ AEiI

Kierunek AiR

Æwiczenia laboratoryjne z fizyki :

Dyfrakcja œwiat³a: wyznaczanie sta³ej siatki dyfrakcyjnej, pomiar d³ugoœci œwiat³a laserowego, wyznaczanie szerokoœci szczeliny

Grupa I, sekcja 5

Les³aw Kaczor

Jaros³aw Olczyk

Gliwice 13.04.19941.Opis teoretyczny.

Dyfrakcja jest to zjawisko polegaj¹ce na uginaniu siê promieni œwietlnych przechodz¹cych w pobli¿u przeszkody, takiej jak np. brzeg szczeliny. Zwykle efekty dyfrakcyjne s¹ ma³e i trzeba ich uwa¿nie szukaæ. Poza tym wiêkszoœæ ¿róde³ œwiat³a to przedmioty rozci¹g³e, wobec czego obraz dyfrakcyjny wytworzony przez jeden punkt Ÿród³a nak³ada siê na obrazy wytworzone przez inne punkty. Wreszcie, zwyk³e ¿ród³a œwiat³a nie s¹ monochromatyczne. Obrazy dla ró¿nych d³ugoœci fali nak³adaj¹ siê na siebie i znów zjawisko jest mniej widoczne. Zjawisko dyfrakcji mo¿na zaobserwowaæ przy przejœciu œwiat³a przez w¹skie szczeliny lub przeszkody, których szerokoœæ jest rzêdu setnych czêœci milimetra. Na ekranie ustawionym za t¹ szczelin¹ obserwujemy smugê œwietln¹ otoczon¹ symetrycznie szeregiem jasnych i ciemnych pr¹¿ków, stanowi¹c¹ obraz dyfrakcyjny szczeliny. Powstanie obrazu dyfrakcyjnego, niezgodne z zasad¹ prostoliniowego rozchodzenia siê promieni, mo¿na wyjaœniæ na podstawie falowej natury œwiat³a. Zgodnie z zasad¹ Huygensa ka¿dy punkt, do którego dochodz¹ fale, staje siê Ÿród³em elementarnych fal kulistych rozchodz¹cych siê wokó³ tego punktu. Fale te interferuj¹c ze sob¹ staj¹ siê przyczyn¹ powstawania jasnych i ciemnych pr¹¿ków. Praktycznie zazwyczaj nie u¿ywa siê pojedynczej szczeliny lecz siatki dyfrakcyjnej. Jest to najczêœciej p³aska p³ytka szklana pokryta równoleg³ymi rowkami, naciêtymi w bardzo ma³ych odleg³oœciach. Rysy p³ytki odgrywaj¹ rolê przes³on, natomiast przerwy miêdzy nimi rolê szczelin przepuszczaj¹cych œwiat³o.

2.Opis æwiczenia.

W æwiczeniu obserwowaliœmy dyfrakcjê na siatce dyfrakcyjnej oraz na pojedynczej szczelinie.

1.W pierwszej czêœci æwiczenia obserwowaliœmy obraz dyfrakcyjny uzyskany przy pomocy siatki dyfrakcyjnej. Siatka by³a umieszczona w spektrometrze i oœwietlona œwiat³em o znanej d³ugoœci. Nale¿a³o zmierzyæ k¹ty ugiêcia dla trzech rzêdów w prawo i w lewo aby na podstawie tych danych i wzoru:

gdzie n -rz¹d pr¹¿ka dyfrakcyjnego

wyznaczyæ sta³¹ siatki. Pomiar trzeciego rzêdu w prawo by³ utrudniony ze wzglêdu na odblaski powsta³e na siatce, wobec czego nie zosta³ przeprowadzony aby nie wprowadzaæ b³êdów do pomiarów. Zamiast k¹ta trzeciego rzêdu zosta³ zmierzony czwarty i osobno ujêty w obliczeniach.

2.Druga czêœæ æwiczenia polega³a na pomiarze d³ugoœci œwiat³a laserowego, która to wartoœæ jest potrzebna do trzeciej czêœci æwiczenia. W celu pomiaru d³ugoœci œwiat³a laserowego nale¿a³o umieœciæ siatkê dyfrakcyjn¹ o sta³ej wyznaczonej w æwiczeniu pierwszym nastêpnie zosta³a zmierzona odleg³oœæ siatki od ekranu oraz po³o¿enia kolejnych pr¹¿ków dyfrakcyjnych na prawo i lewo. Nastêpnie zosta³a wyliczona d³ugoœæ œwiat³a laserowego ze wzoru:

3. Trzecia czêœæ æwiczenia polega³a na wyznaczeniu szerokoœci szczeliny na której ulega³o ugiêciu œwiat³o laserowe o d³ugoœci wyliczonej w drugim æwiczeniu. Pomiar obrazu dyfrakcyjnego by³ przeprowadzony metod¹ fotoelektryczn¹, pomiary by³y dokonywane co 0.083 mm co zapewnia dok³adne odczytanie pozycji kolejnych minimum obrazu dyfrakcyjnego. Nastêpnie zosta³a obliczona szerokoœæ szczeliny ze wzoru warunku minimum :

wiêc :

czyli: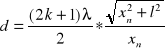

3.Tabela pomiarowa.

Tabela pomiarowa nr. 1

Pomiary kątów ugięcia na siatce dyfrakcyjnej

0 = 179°40'

B³¹d pomiaru  = 10'

Lp.	n=1		n=2				n=3		n=4
	1l'	1p		2l	2p	3l		4p
1	186°20'	173°40'		193°00'	167°50'	200°20'		152°30'
2	186°20'	173°40'		193°00'	167°50'	200°00'		152°40'
3	186°00'	173°10'		193°00'	167°40'	200°00'		152°20'
4	186°00'	173°40'		193°00'	166°40'	200°00'		152°10'
5	186°00'	173°30'		193°00'	167°00'	200°00'		152°00'

Tabela pomiarowa nr. 2

Pomiary odchyleń światła laserowego na siatce dyfrakcyjnej.

Odleg³oœæ od ekranu l = 125 cm

Ze wzglêdu na rozmycie plamki na ekranie oraz rêczny pomiar odchyleñ dok³adnoœæ pomiaru nie jest wiêksza ni¿ 5 mm.

n	x [cm] (lewo)	x [cm] (prawo)
1	15.5	15.5
2	32.5	32.7
3	-	49.5

4.Opracowanie wyników pomiarów.

1. Wyznaczanie sta³ej siatki dyfrakcyjnej.

Obliczanie œrednich k¹tów ugiêcia. Najpierw zosta³y obliczone œrednie wartoœci k¹tów ugiêcia w prawo i w lewo na podstawie danych z tabeli nr. 1. B³êdy zosta³y wyznaczone przy pomocy rozstêpu z próby.

n=1

n=2

n=3

n=4

1lœr'

1pœr

2lœr

2pœr

3lœr

4pœr

186°12'

173°32'

193°00'

167°24'

200°4'

152°20'

Da

12'

22'

0'

44'

16'

20'

Nastêpnie zosta³y policzone k¹ty ugiêcia dla poszczególnych rzêdów. Dla 1 i 2 rzêdu ze wzoru:

Dla rzêdów 3 i 4 ze wzglêdu pomiaru odchylenia tylko w jedn¹ stronê zastosowany zosta³ wzór:

B³êdy zosta³y obliczone metod¹ ró¿niczki zupe³nej. Otrzymano nastêpuj¹ce wyniki :

1 = 6°18' ± 17'

2 = 12°48' ± 22'

a3 = 20°24' ± 10'

4 = 27°20' ± 20'

Obliczenie sta³ej siatki dyfrakcyjnej:

Sta³e siatki dyfrakcyjnej dla poszczególnych rzêdów zosta³y wyliczone ze wzoru:

gdzie  = 589.3 nm - œrednia d³ugoœæ fali ¿ó³tego dubletu sodu

B³êdy zosta³y policzone z ró¿niczki zupe³nej:

gdzie n - b³¹d pomiaru k¹tów przeliczony na miarê ³ukow¹.

n=1

n=2

n=3

n=4

Nastêpnie przy pomocy œredniej wa¿onej zosta³a obliczona œrednia wartoœæ sta³ej siatki oraz jej b³¹d :

d=5.107*10-6 ± 3.167*10-8

Pomiar d³ugoœci œwiat³a laserowego.

Na podstawie danych z tabeli nr. 2 oraz uprzednio wyliczonej sta³ej siatki wyliczamy d³ugoœæ œwiat³a œwiat³a laserowego ze wzoru:

gdzie : d -sta³a siatki dyfrakcyjnej

l - odleg³oœæ siatki od ekranu

xn -odleg³oœci kolejnych pr¹¿ków od pr¹¿ka zerowego na ekranie

n - rz¹d pr¹¿ka

B³êdy zosta³y obliczone za pomoc¹ ró¿niczki zupe³nej:

gdzie d -b³¹d wzglêdny sta³ej siatki

x = 5mm- b³¹d odczytu x

1 l,p) x=15.5 cm

2 l) x=32.5 cm

2 p) x=32.7 cm

3) x=49.5 cm

Nastêpnie za pomoc¹ œredniej wa¿onej zosta³a wyliczona œrednia d³ugoœæ œwiat³a oraz jej b³¹d :

œr = 634.623 ± 6.16nm

Wyznaczenie szerokoœci szczeliny :

Z wyników pomiaru metod¹ fotoelektryczn¹ zosta³y odczytane nastêpuj¹ce po³o¿enia minimum (wzglêdem pocz¹tku podzia³ki):

Rz¹d	x [mm] (lewo)	x [mm] (prawo)
0	6.8	15.684
1	2.684	20.350

Oraz po³o¿enie najwiêkszego maksimum :

xmax = 10.850 mm

Z tych danych zosta³y obliczone odleg³oœci kolejnych minimów od osi uk³adu :

1 l	0 l	0 p	1 p
8.167 mm	4.05 mm	4.834 mm	9.5 mm

Które zosta³y wstawione do wzoru jako x :

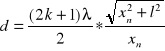
B³êdy zosta³y policzone z ró¿niczki zupe³nej :

gdzie: Dl - b³¹d pomiaru l

Dx = 0.048 mm niepewnoϾ pomiarowa x

1 l) x = 4.05 mm

1 p) x = 4.834 mm

2 l) x = 8.167 mm

2 p) x = 9.5 mm

Za pomoc¹ œredniej wa¿onej obliczono œredni¹ szerokoœæ szczeliny oraz jej b³¹d :

dœr = 4.576*10-5 ± 3.489*10-7 m

Ze wzglêdu na du¿y rozstêp kolejnych obliczeñ w stosunku do œredniej (du¿o wiêkszy ni¿ wyliczony b³¹d), bardziej odpowiedni¹ metod¹ obliczenia b³êdu dœr wydaje siê metoda rozstêpu z próby:

dœr = 0.046 ± 00013 mm

5.Podsumowanie.

Du¿y b³¹d w wyniku najprawdopodobniej jest spowodowany niezbyt precyzyjnym odczytaniem po³o¿enia maksimum w metodzie fotoelektrycznej spowodowane "postrzêpieniem" miejscu odczytu.

---