Funkcja kwadratowa.

Zad.1 Naszkicować wykres funkcji :

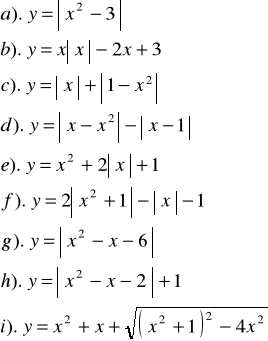
Zad.2 Znaleźć funkcję
wyrażającą liczbę pierwiastków równania

w zależności od parametru
.

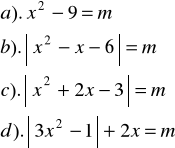
Zad.3 Wyznaczyć największą i najmniejszą wartość funkcji w podanym

przedziale

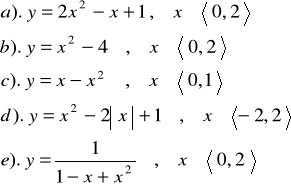
Zad.4 Dla jakiej wartości parametru
równanie :

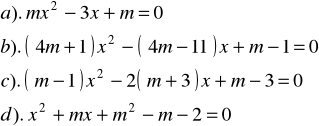
ma jedno rozwiązanie ?

Zad.5 Wiadomo, że
i
są pierwiastkami równania
.

Nie rozwiązując równania, obliczyć wyrażenie

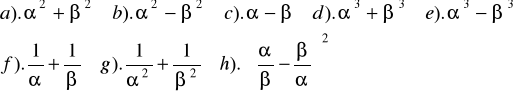
Zad.6 Dla jakich wartości parametru
równanie
ma dwa

różne pierwiastki rzeczywiste spełniające warunek :
?

Zad.7 Rozwiązać równanie :

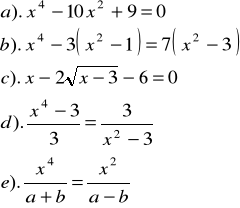
Zad.8 Dla jakich wartości parametru
wykresy funkcji

i
mają przynajmniej jeden punkt wspólny ?

Zad.9 Rozwiązać nierówność :

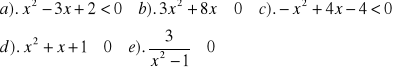
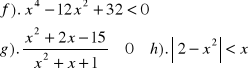
Zad.10 Rozwiązać układ nierówności :

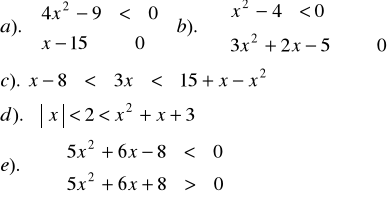
Zad.11 Dla jakich wartości parametru
nierówność

jest prawdziwa dla każdej liczby rzeczywistej x ?

Zad.12 Dla jakich wartości
układ nierówności

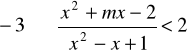
jest spełniony dla wszystkich wartości x ?

Zad.13 Dla jakich wartości parametru
funkcja

ma wartość ujemną dla każdej

rzeczywistej wartości zmiennej x ?

Zad.14 Dla jakich wartości parametru
równanie

ma dwa różne pierwiastki mniejsze od 4?

Zad.15 Dla jakich wartości parametru
suma odwrotności pierwiastków

równania
jest dodatnia?

Zad.16 Dla jakich wartości parametru
równanie

ma dwa różne pierwiastki dodatnie ?

Zad.17 Dla jakich wartości parametru
równanie

ma dwa pierwiastki rzeczywiste o jednakowych znakach ?

Zad.18 Dla jakich wartości parametru
pierwiastki równania

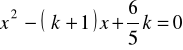
są równe sinusowi i cosinusowi tego samego

kąta ostrego ?

Zad.19 Dla jakich wartości
rozwiązanie układu równań

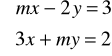
spełnia warunki
?

Zad.20 Znaleźć maksimum funkcji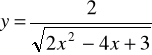
.

Zad.21 Rozwiązać i zilustrować graficznie układ równań :

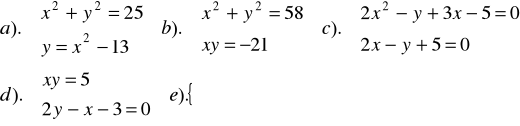
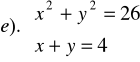
Zad.22 Dla jakich wartości parametru
układ równań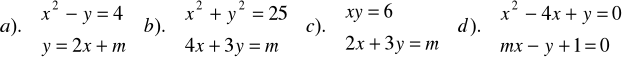

ma dokładnie jedno rozwiązanie?

Zad.23 Rozwiązać układ równań :
. Przeprowadzić dyskusję ze względu na parametr m. .

Zad.24 Rozwiązać graficznie układ

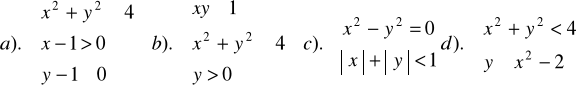
Zad.31. Rozwiązać układ równań :

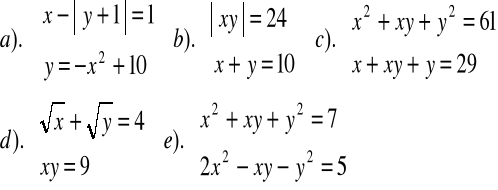
Zad.32. Rozwiązać rachunkowo i graficznie układ równań :

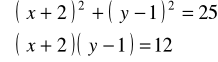
Zad.33. Podać interpretację geometryczną układu nierówności :

.

---