ĆWICZENIA WYKONYWANE NA ZAJĘCIACH

1. Tworzenie arkusza obliczającego średnie oraz skrajne różnice wyników testów za pomocą formuł tablicowych.

Należy utworzyć zamieszczoną poniżej tabelę i wypełnić jej początkowe wiersze nazwiskami i wynikami poszczególnych testów. Do pól ostatnich trzech wierszy należy wpisać formuły tablicowe obliczające średnie zmiany oraz największe spadki i wzrosty wyników testów dla każdej pary testów.

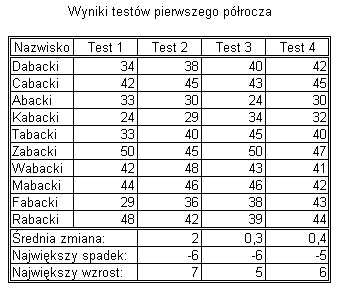
2. Tworzenie arkusza obliczającego liczność występowania różnych rodzajów ocen.

Należy utworzyć zamieszczone poniżej tabele i wypełnić je przykładowymi danymi za wyjątkiem kolumn:„Ogółem”, ”Prz. 1”,”Prz. 2”, ”Prz. 3” oraz „Prz. 4”, w tabeli z prawej strony. W komórkach wymienionych kolumn należy wpisać formuły tablicowe obliczające liczność wystąpień poszczególnych rodzajów ocen w tabeli z lewej strony dla wszystkich ocen (kolumna Ogółem) i poszczególnych przedmiotów (dla ułatwienia zapisu formuł i późniejszej modyfikacji tabeli można fragmentom tabeli zawierającym oceny z poszczególnych przedmiotów oraz wszystkie oceny nadać nazwy i wykorzystać je w zapisie formuł).

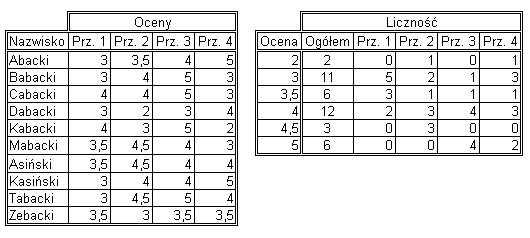
3. Obliczanie iloczynu macierzy, wyznacznika oraz wyznaczanie macierzy odwrotnej.

Wykorzystując poznane funkcje działające na tablicach oraz umiejętność konstruowania formuł tablicowych należy:

1. obliczyć iloczyny macierzy:

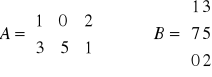
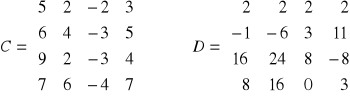
2. sprawdzić czy macierze kwadratowe są nieosobliwe i jeżeli tak, to wyznaczyć dla nich macierze odwrotne,

3. dla macierzy, dla których można wyznaczyć macierze odwrotne obliczyć iloczyn macierzy i macierzy odwrotnej, a następnie elementy macierzy wynikowej poddać takiej konwersji (zaokrąglić), aby otrzymana macierz była macierzą jednostkową.

4. Tworzenie formuł tablicowych, których wynik jest zapisywany w jednej komórce.

Należy utworzyć tabelę liczb dodatnich i ujemnych o rozmiarach co najmniej 5 wierszy i 6 kolumn, a następnie w komórkach arkusza położonych poniżej tej tabeli należy wpisać formuły tablicowe obliczające następujące wielkości:

• sumę wszystkich liczb ujemnych zawartych w tablicy,

• pierwiastek drugiego stopnia z sumy wszystkich liczb dodatnich zawartych w tablicy,

• średnią wszystkich liczb z tablicy, których wartość jest większa lub równa 5,

• sumę wszystkich liczb dodatnich z pierwszej, trzeciej i piątej kolumny,

• iloczyn wszystkich liczb z drugiej, czwartej i szóstej kolumny, których wartość jest mniejsza niż 10.

5. Tworzenie arkusza umożliwiającego sprawdzanie czy podane nazwisko występuje w utworzonej wcześniej liście.

Należy wpisać zamieszczone na następnej stronie teksty objaśniające zawartość komórek oraz tabelę z przykładowymi nazwiskami. Komórce umieszczonej po tekście „ Podaj szukane nazwisko” należy nadać nazwę. W komórce umieszczonej na prawo od tabeli należy wpisać formułę tablicową, która poszukuje podanego nazwiska w liście nazwisk i w zależności od wyniku poszukiwania wyświetla komunikat „Nazwisko jest na liście” lub „Nazwiska brak w liście”. Na wydruku przedstawiono wynik działania wymienionej formuły w przypadku, gdy nazwisko nie zostało odszukane w liście.

Projektując formułę przeszukującą listę nazwisk należy pamiętać o tym, że program podejmuje decyzje (funkcja JEŻELI) oraz o tym, że negatywny wynik sprawdzania kolejnej komórki obszaru może „zamazać” wynik poprzedniego sprawdzenia (zastosować funkcję LUB w funkcji JEŻELI).

ĆWICZENIA WYKONYWANE SAMODZIELNIE

6. Traktując jako źródłową tabelę z punktu 5 bieżącego ćwiczenia, w komórkach arkusza leżących poniżej tabeli należy wprowadzić formuły tablicowe obliczające następujące wielkości:

• sumę ilości liter we wszystkich nazwiskach wpisanych do tablicy,

• ilość znaków w najdłuższym nazwisku,

• ilość znaków w najkrótszym nazwisku,

• średnią długość nazwiska,

a następnie zmieniając dowolnie wybrane nazwiska należy zaobserwować, czy wpisane formuły poprawnie obliczają wyniki po zmianach wprowadzonych do tabeli.

7. Wykorzystując poznane funkcje działające na tablicach oraz umiejętność konstruowania formuł tablicowych należy:

1. obliczyć iloczyny macierzy:

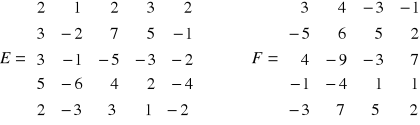
2. sprawdzić czy macierze kwadratowe są nieosobliwe i jeżeli tak, to wyznaczyć dla nich macierze odwrotne,

3. dla macierzy, dla których można wyznaczyć macierze odwrotne obliczyć iloczyn macierzy i macierzy odwrotnej, a następnie elementy macierzy wynikowej poddać takiej konwersji (zaokrąglić), aby otrzymana macierz była macierzą jednostkową.

8. Algorytm rozwiązywanie układu n równań liniowych o n niewiadomych.

Poznane funkcje programu EXCEL działające na tablicach wykorzystamy teraz do rozwiązania układu równań liniowych - zadania, które spotyka się nie tylko w matematyce, lecz także przy rozwiązywaniu problemów ekonomicznych czy technicznych. Załóżmy, że mamy następujący układ trzech równań liniowych o trzech niewiadomych:

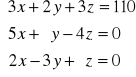
i do jego rozwiązania zastosujemy wzory Cramera. Algorytm ten polega na:

1. ułożeniu macierzy ze współczynników równania stojących przy niewiadomych, a następnie obliczeniu wyznacznika W tej macierzy (wyznacznik ten nazywany jest wyznacznikiem głównym); zapis macierzy i sposób obliczenia wyznacznika przedstawia poniższy rysunek

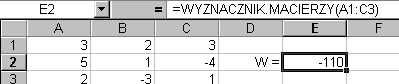
ponieważ wyznacznik główny jest różny od zera, rozwiązywany układ jest układem oznaczonym (posiada rozwiązanie).

2. wstawieniu kolumny wyrazów wolnych w miejsce pierwszej kolumny, gdzie znajdowały się współczynniki stojące przy niewiadomej x i obliczeniu następnego wyznacznika Wx:

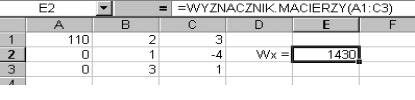
3. wstawieniu kolumny wyrazów wolnych w miejsce drugiej kolumny, gdzie znajdowały się współczynniki stojące przy niewiadomej y i obliczeniu wyznacznika Wy:

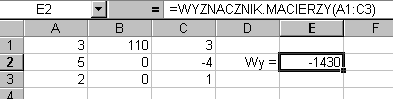
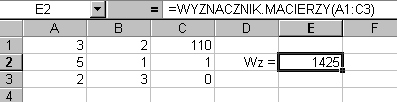
4. wstawieniu kolumny wyrazów wolnych w miejsce trzeciej kolumny, gdzie znajdowały się współczynniki stojące przy niewiadomej z i obliczeniu wyznacznika Wz:

5. obliczeniu rozwiązania układu według poniższych wzorów:

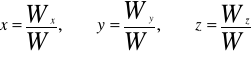
9. Rozwiązywanie układów n równań liniowych o n niewiadomych.

Wykorzystując poznane wzory Cramera należy sprawdzić czy istnieją, a jeżeli tak, to znaleźć rozwiązania następujących układów równań:

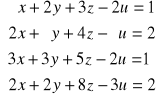
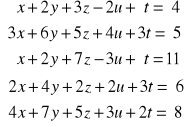
WSE Ekonomiczny Informatyka w zarządzaniu przedsiębiorstwem STUDIA ZAOCZNE

Temat 00Y: Funkcje i formuły tablicowe.

Strona 1 z 4

---